激光惯性约束聚变（ICF）是实验室实现可控聚变的重要途径之一，近期该领域取得了一系列重要突破，从DT聚变放能大于DT燃料吸能^[1]到燃烧等离子体的实现^[2-3]，再到接近点火条件的约1.37 MJ聚变放能的历史性突破^[4-6]。当然，要实现更高增益的聚变点火，还需对很多物理问题有更深入的理解，ICF相关的非平衡动理学效应就是此类问题之一。在ICF研究中，人们一般使用基于局域热动平衡假设的单辐射流体对整个物理过程进行模拟，但是ICF等离子体参数跨度非常大，密度从10¹⁹ cm⁻³到10²⁵ cm⁻³、温度从0.01 keV到10 keV、物质组分从轻离子（D，T等）到高Z离子（Au，W等），在高温、低密区域局域热动平衡假设并不适用，一些非平衡动理学效应可能起到不可忽略的作用，例如离子分离、扩散、贯穿、界面电磁场等^[7-14]，可能与“能量丢失”^[15]、芯部压缩对称性异常^[16-17]等现象有关^[18]。

中国工程物理研究院的科研人员首次在ICF黑腔等离子体界面区域发现了静电冲击波非平衡效应^[19-22]。纳秒激光与腔壁作用后产生高温高密度膨胀的Au等离子体，与辐射烧蚀的低温低密度靶丸等离子体相遇，界面强烈的电子压力梯度驱动出无碰撞静电冲击波。该冲击波能以二倍冲击波速度反射靶丸等离子体中的低Z离子（C，H，D等）达到几十上百keV（即超热离子），这些超热离子返回到靶丸可能会对靶丸的压缩对称性造成影响^[19-20]。目前，反射离子能谱信息都是模拟给出的，缺乏实验的直接测量。直接测量离子能谱对于校验程序的准确性、评估超热离子能量份额都十分重要。

皮秒、飞秒激光驱动的相对论无碰撞静电冲击波的运动速度非常快（可达数千km·s⁻¹），反射离子能量可达到MeV量级，利用汤姆逊离子谱仪进行测量已有很多相关报道^[23-25]。而纳秒激光驱动的非相对论无碰撞静电冲击波运动速度较慢（数百km·s⁻¹），被反射的D离子能量低到20 keV附近，如此低能的离子容易受到各方面因素的影响，在黑腔环境中难以进行直接测量（被靶丸及黑腔腔壁阻挡）。为了测量离子能谱，可以利用喷气靶设计分解实验^[26]，喷气靶设计的优点是，去掉了靶丸及黑腔的阻挡，冲击波反射的超热离子会直接进入谱仪被测量。由于反射离子会受到靶室残余气体和喷气气体的散射，导致能量的损失和运动方向的改变，离子能量越低，预期受到的影响越大，因此，低能离子在被测量前还有被影响的可能。为了尽量降低实验风险，本文利用Geant4程序对整个过程进行蒙卡建模计算，评估靶室残余气体和喷气气体对反射离子能谱测量的影响。

1.   低能汤姆逊离子谱仪的设计及Geant4计算模型的构建

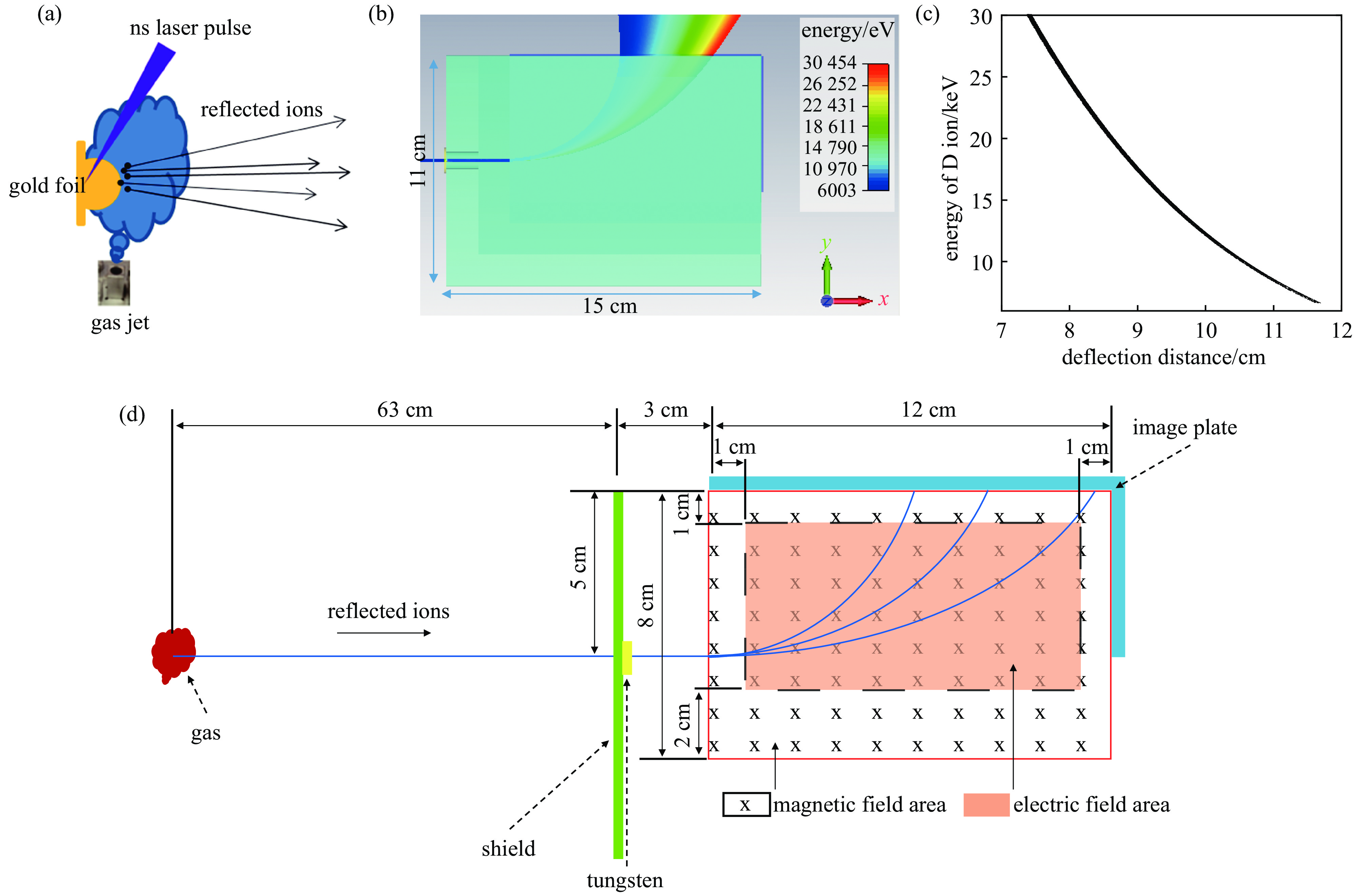
喷气靶示意图如图1（a）所示，左侧的Au平面靶代替黑腔腔壁，侧下方超音速喷嘴喷出的气体代替腔内充气或者靶丸等离子体。为了测量20 keV附近的D离子，设计了低能汤姆逊离子谱仪，如图1（b）所示，谱仪长15 cm，高11 cm，磁铁长12 cm，高8 cm，与谱仪右边缘和上边缘对齐，电极板长10 cm，高5 cm，边缘距离谱仪右边缘和上边缘各1 cm，谱仪准直孔直径200 μm，中心距离谱仪上边缘5 cm，L型IP成像板放置于谱仪边缘。磁场设计强度0.3 T，使用CST电磁仿真软件对6～30 keV的D离子束在整个系统中的传输过程进行了模拟计算，模拟得到D离子在低能汤姆逊离子谱仪中的运动轨迹如图1（b）所示。对D离子能量及其在IP成像板上的位置信息进行统计（原点对应于谱仪准直孔位置），给出了D离子能量与偏转距离的关系，如图1（c）所示。15 keV能量的D离子在IP板上的偏转距离在9.435 cm附近，该位置处由于谱仪准直孔导致的能量上下限分别为15.18 keV和14.81 keV，从而得到该位置处的能谱分辨为2.47%。

图  1  （a）喷气靶示意图，（b）低能汤姆逊离子谱仪结构及D离子运动轨迹，（c）D离子能量与偏转距离的关系，（d）谱仪的Geant4模型示意图

Figure  1.  (a)Schematic diagram of gas-jet target,(b)structure of the low-energy Thomson ion spectrometer and trajectories of D ions, (c) the relationship between the energy of D ion and the deflection distance, (d) schematic diagram of Geant4 model of the spectrometer

下载: 全尺寸图片 幻灯片

根据谱仪结构进行Geant4建模，如图1（d）所示。红色区域表示喷气靶产生的喷气气体，静电冲击波在其中产生并反射离子，绿色区域是谱仪前表面屏蔽体，铅材料，5 mm厚，开有直径1 mm的孔，黄色区域为钨材料，5 mm厚，开200 μm直径的准直孔，准直孔与谱仪前表面屏蔽体的开孔同心，蓝色是L型IP成像板。磁场位于图中12 cm×8 mm的红色方框区域内，磁场方向垂直纸面向里（×），电场位于图中10 cm×5 cm的橙色区域，方向垂直纸面向里，相关尺寸已在图中标示，磁场大小设置为0.3 T，电场大小设置为6 kV/m。实验测量过程中，整个系统是放置在真空靶室内，靶室残余气体（空气）充满整个建模区域。模拟中采用Geant4的Shielding模块，主要涉及电场相互作用，离子与气体分子的碰撞电离作用（非弹性散射）。

2.   模拟结果与分析

2.1   靶室残余气体的影响

高功率纳秒激光装置的靶室体积通常大于10 m³，靶室真空度进入10⁻²～10⁻³ Pa量级即可打靶，更高的真空度要求很难做到，并且会显著增加打靶等待时间。因此，有必要研究靶室残余气体对反射离子能谱测量的影响。简单起见，考虑单能D离子源，离子源距离谱仪前表面63 cm，设置为均匀圆形面源，半径2 mm（纳秒激光打靶焦斑直径一般在200 μm，但烧蚀产生的膨胀等离子体及驱动的静电冲击波空间尺度可以达到mm量级），0.23°内各向同性均匀发射。

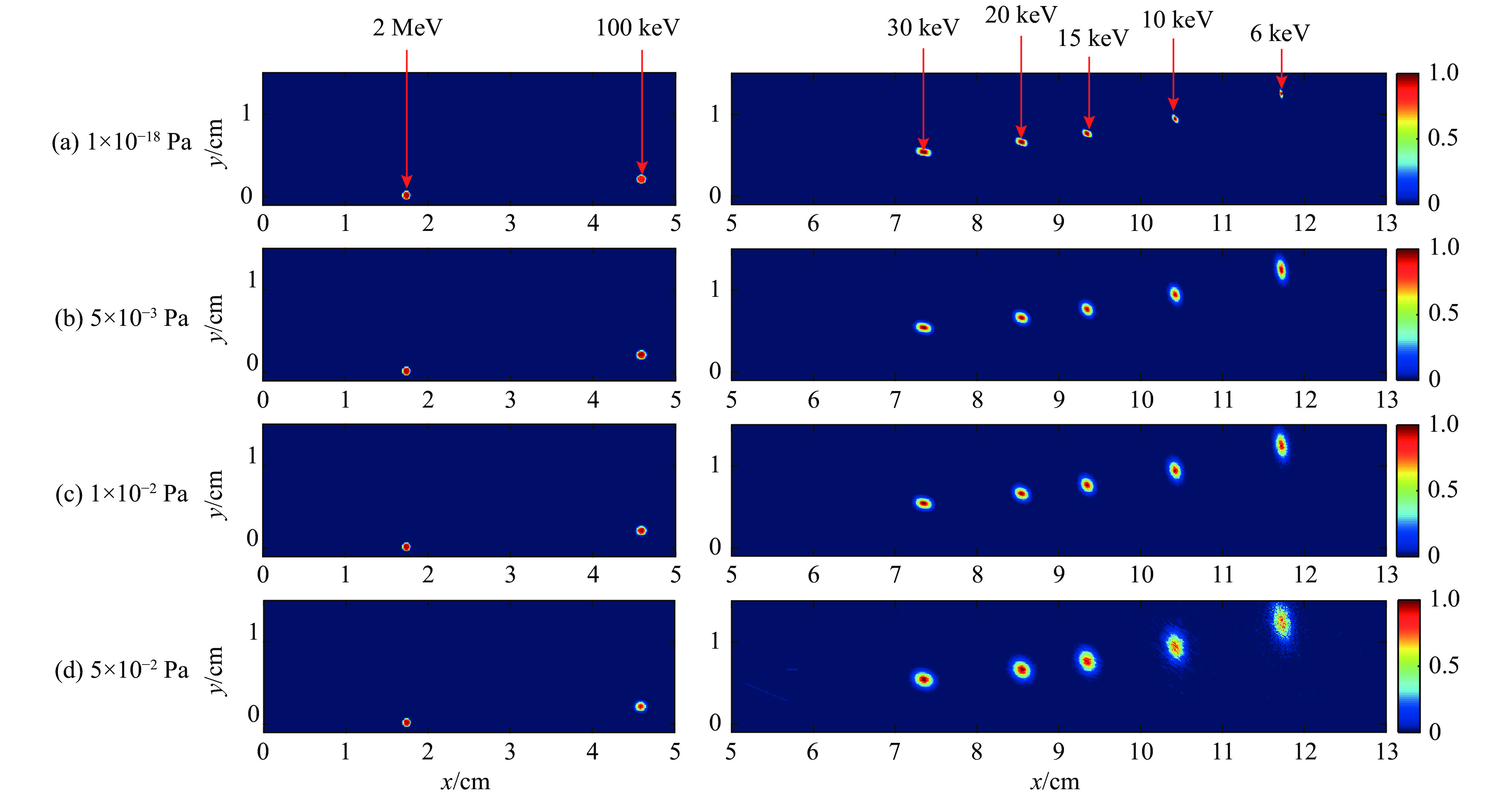
图2为靶室真空度分别为1×10⁻¹⁸, 5×10⁻³, 1×10⁻², 5×10⁻² Pa四种情况下，不同能量D离子源（2000, 100, 30, 20, 15, 10, 6 keV）在IP成像板处的流强信号（各自归一化）。原点对应于谱仪准直孔位置。x方向为谱仪的磁场方向，区域(0～5 cm)为模型中竖直段IP，区域(5～13 cm)为模型中水平段IP，能量越小的D离子在谱仪磁场中偏转半径越小，对应的x值越大。y方向为谱仪的电场方向。靶室真空度1×10⁻¹⁸ Pa可以认为是没有靶室残余气体的极限真空情况，其数据反映的是D离子源及谱仪本身的性质。直观看来，对于2 MeV的D离子，甚至100 keV的D离子，IP板上的信号二维分布基本不受靶室真空度变化的影响，说明靶室残余气体对100 keV以上D离子的散射作用很弱。因此，MeV甚至100 keV量级离子的测量不需要考虑靶室残余气体的影响，已有的MeV量级离子测量的文献报道中也确实没有考虑过靶室残余气体的影响。但随着D离子能量的进一步降低，信号分布范围逐渐受到靶室真空度的影响，D离子能量越低受到的影响越明显，这主要是因为D离子受靶室残余气体散射作用的影响，散射会一定程度改变入射D离子的运动方向，从而增大探测面IP板上的分布展宽，越低能的D离子受散射导致的角度变化相对越大，因此在IP板上的空间展宽也越大。

图  2  不同能量的单能D离子源在IP成像板处的流强信号

Figure  2.  Current intensities of monoenergetic D ions at the positions of image plates

下载: 全尺寸图片 幻灯片

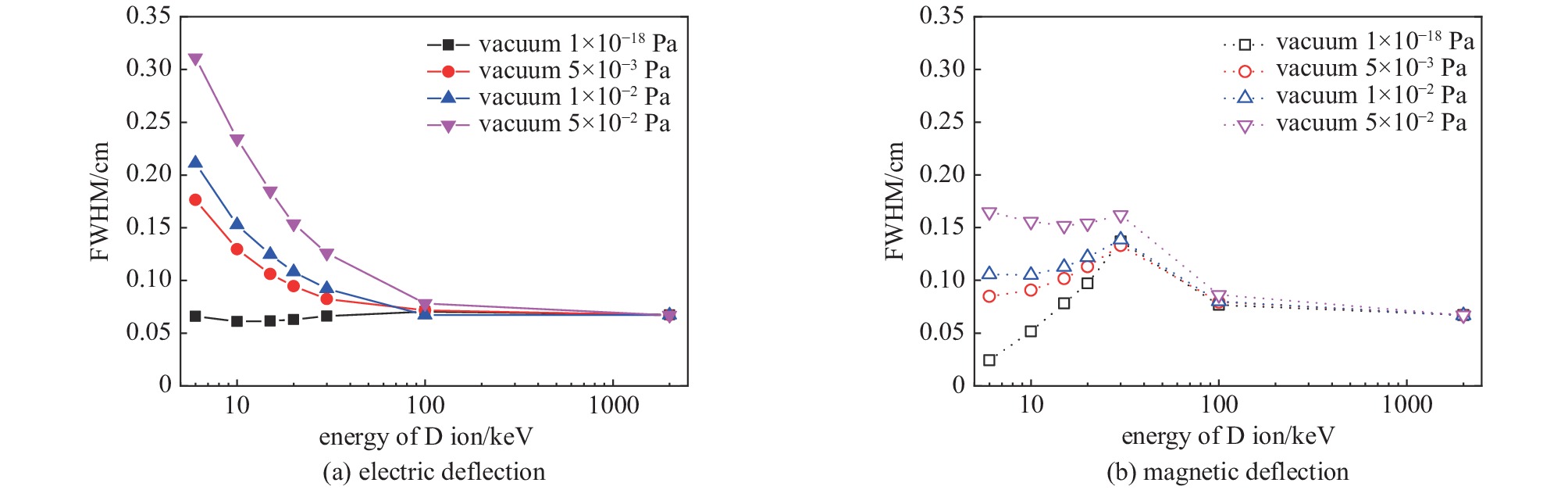
下面将定量研究展宽的变化规律，首先讨论IP板上信号在电场方向（y方向）的变化规律。图3（a）给出图2（c）中不同能量D离子数量在y方向的归一化分布（x方向积分处理），对该分布进行高斯拟合，用高斯分布的半高全宽表征分布的展宽，图4（a）给出了不同残余气体条件下，D离子分布半高全宽随离子能量的变化趋势。靶室真空度1×10⁻¹⁸ Pa情况下，信号在电场方向的半高全宽基本不随D离子能量的变化而变化（图中实心方框黑实线），保持在0.067 cm附近，这是离子源本身空间尺寸通过谱仪准直孔小孔成像导致的，反映的是源的大小。靶室残余气体气压增加后，2 MeV和100 keV能量D离子的半高全宽基本不受靶室真空度变化的影响。在MeV量级离子的汤姆逊离子谱仪测量报道中^[23-25]，通过加电场，不同荷质比的离子形成一条条分开的谱线从而获得区分，谱线在电场方向的展宽很弱且在不同信号区域没有明显变化。这与我们关于100 keV及以上能量离子空间展宽可忽略的结论是一致的。但随着D离子能量进一步降低，半高全宽随靶室气压的增加而增加。对于6 keV能量的D离子，其半高全宽从靶室真空度1×10⁻¹⁸ Pa条件下的0.066 cm逐渐增加到5×10⁻² Pa下的0.311 cm。实际实验中，往往不止一种离子，不同荷质比的离子需要通过不同的谱线进行区分，谱线展宽增加了谱线间发生交叠的风险。所以，针对低能离子的测量，实际实验中应尽量降低靶室气压（如到达5×10⁻³ Pa甚至更低）用于减少靶室残余气体的影响，同时适当增加谱仪电压用以拉开谱线间的间距。

图  3  靶室真空度1×10⁻² Pa情况下信号在电场和磁场方向的分布

Figure  3.  Distributions of the signals in the electric and magnetic deflection when the air pressure of the vacuum target chamber is 1×10⁻² Pa

下载: 全尺寸图片 幻灯片

图  4  信号在电场和磁场方向的半高全宽

Figure  4.  Full widths at half maximum of the signals in the electric and magnetic deflection

下载: 全尺寸图片 幻灯片

类似的，将图2中的离子信号沿谱仪电场方向（y方向）积分后归一化，得到信号在磁场方向（x方向）的分布（靶室真空度1×10⁻² Pa情况下见图3（b）），再对分布进行高斯拟合，得到信号在磁场方向分布的半高全宽见图4（b）所示。靶室真空度1×10⁻¹⁸ Pa条件下，信号在磁场方向的半高全宽随D离子能量的降低先增加后降低（图中空心方框黑点线），这是跟谱仪结构设计的能谱分辨相关联的。2 MeV及100 keV能量D离子的半高全宽基本不受靶室真空度变化的影响。但随着D离子能量的进一步降低，靶室真空度对半高全宽的影响逐渐体现出来。对于6 keV的D离子，1×10⁻¹⁸ Pa气压下半高全宽为0.024 cm，5×10⁻³ Pa气压下半高全宽增加到0.085 cm（扩展到了约3.5倍），5×10⁻² Pa气压下半高全宽增加到0.165 cm（扩展到了约6.9倍）。谱仪的磁场方向是能量方向，通过信号在磁场方向的位置去对应离子的能量，从而得到离子能谱。在不受靶室残余气体影响的情况下（如MeV离子的测量），测量能谱的误差主要来源于谱仪自身的能谱分辨。而对于10 keV能段的D离子，如模拟中显示，靶室残余气体会导致测量信号在磁场方向展宽，这个展宽可以是谱仪自身谱分辨导致展宽的好几倍。对于纳秒激光驱动的非相对论无碰撞静电冲击波，预期的反射D离子能谱具有单能峰结构，而能峰的位置就在10 keV左右。因此，反射离子能谱在靶室残余气体影响下会展宽，因此IP板测量到的能谱展宽要比实际的展宽更宽。从图4（b）可以看出，靶室残余气体导致的测量信号展宽是随靶室气压和离子能量的变化而变化的，如何从测量到的信号反解出真实的反射离子能谱（未经过靶室残余气体的散射）是进一步研究的方向。

2.2   喷气气体的影响

现在考虑喷气气体本身对反射离子能谱测量的影响。对于固定条件的Au靶和纳秒激光，其在不同密度喷气气体中驱动静电冲击波的运动速度是不同的，相对应的反射离子能量也是不同。流体模拟虽然不能给出静电冲击波电场结构等动理学信息，但是可以定性给出冲击波的宏观运动趋势。我们利用Flash磁流体程序^[27]模拟了纳秒激光（3 ns方波，能量1800 J，靶焦斑直径200 μm）烧蚀Au平面靶产生的膨胀等离子体在喷气气体（氘气）中驱动流体冲击波的运动情况。喷气气体密度设置为0.00265，0.00795，0.029 mg/cm³时对应的冲击波运动速度大约为694，602，497 km/s。流体程序虽然不能给出反射离子能谱信息，但我们可以利用反射离子能量对应于二倍冲击波速度的定性关系^[28]，给出反射D离子能量分别为20，15，10 keV。如引言中所述，冲击波在喷气气体中形成后一边传播一边产生反射离子，产生的反射离子需要穿出喷气气体，越先被反射的离子需要穿过的喷气气体区域越长。简单起见，模拟中设置半径2 mm（冲击波空间尺度）长1 mm（冲击波传播方向）的圆柱体氘气区域作为冲击波形成后传播和反射离子的区域，在其中设置均匀分布的单能D离子源（运动方向为圆柱体长度方向，即冲击波传播方向），用以模拟在冲击波传播路径上被反射的离子。图5（a）给出了20 keV，15 keV，10 keV（对应的圆柱体氘气区域氘气密度分别设置为0.00265，0.00795, 0.029 mg/cm³，靶室真空度设置为1×10⁻¹⁸ Pa）单能D离子最终在IP成像板处的流强信号（各自归一化）。与图2（a）相比（不考虑喷气气体，靶室真空度1×10⁻¹⁸ Pa），有喷气气体后信号在谱仪磁场方向发生向右的拖尾（向右是能量降低的方向）。图5（b）中红线给出了信号在谱仪磁场方向的分布（沿电场方向积分），而黑线则是不考虑喷气气体的情况（与图2（a）中信号对应）。黑线基本是左右对称的高斯分布，而红线则相对于黑线右移并向右拖尾。信号右移是因为离子在喷气气体中损失能量。而不同区域产生的D离子在喷气气体中穿过的距离不同，穿过的距离越大损失的能量越大，运动方向的改变也越大，进入准直孔的数量越小，所以信号强度减弱，导致整个信号向右侧低能方向拖尾。

图  5  （a）考虑喷气气体后D离子在IP成像板处的流强信号，（b）考虑喷气气体前（黑线）后（红线）信号在磁场方向的分布

Figure  5.  (a) Current intensities of D ions at the positions of image plates after considering the gas jet, (b) the distributions of the signals in the magnetic deflection before (black line) and after (red line) considering the gas jet

下载: 全尺寸图片 幻灯片

3.   结　论

本文利用Geant4程序建模，研究了靶室残余气体和喷气气体对纳秒驱动的非相对论无碰撞静电冲击波反射离子能谱测量的影响。对于高能D离子（100 keV量级及以上），谱仪测量信号不受靶室残余气体的影响。而对于10 keV量级的D离子，由于受到靶室残余气体的散射，谱仪信号在电场和磁场方向均发生展宽，残余气体气压越高，展宽越严重。另外，由于冲击波在喷气气体中一边传播一边反射离子，被反射的离子需要穿出喷气气体，喷气气体对10 keV量级D离子的散射会导致离子能量的损失，越早产生的离子需要穿过的气体区域越长，损失的能量越大，运动方向的改变越大，进入准直孔的离子数量越少、信号强度越弱，最终导致谱仪测量信号向低能区域移动并拖尾，能谱偏离真实的反射离子能谱。该研究有助于提前规避部分实验风险，例如，实验中往往不止一种离子，谱仪信号在电场方向的展宽会带来不同荷质比离子谱线发生交叠的风险，这就需要尽量降低靶室气压以及适当增加谱仪电压以降低风险。另一方面，反射离子能谱的精确测量对于评估黑腔中腔壁与靶丸冕区/填充气体界面动理学效应中产生超热离子的能量份额非常重要，为了获得真实的反射离子能谱，需要扣除靶室残余气体和喷气气体的影响，这将是我们下一步的研究方向。

图  1  四路超短脉冲光纤相干阵列的系统结构

下载: 全尺寸图片 幻灯片

图  2  实验结果图

下载: 全尺寸图片 幻灯片