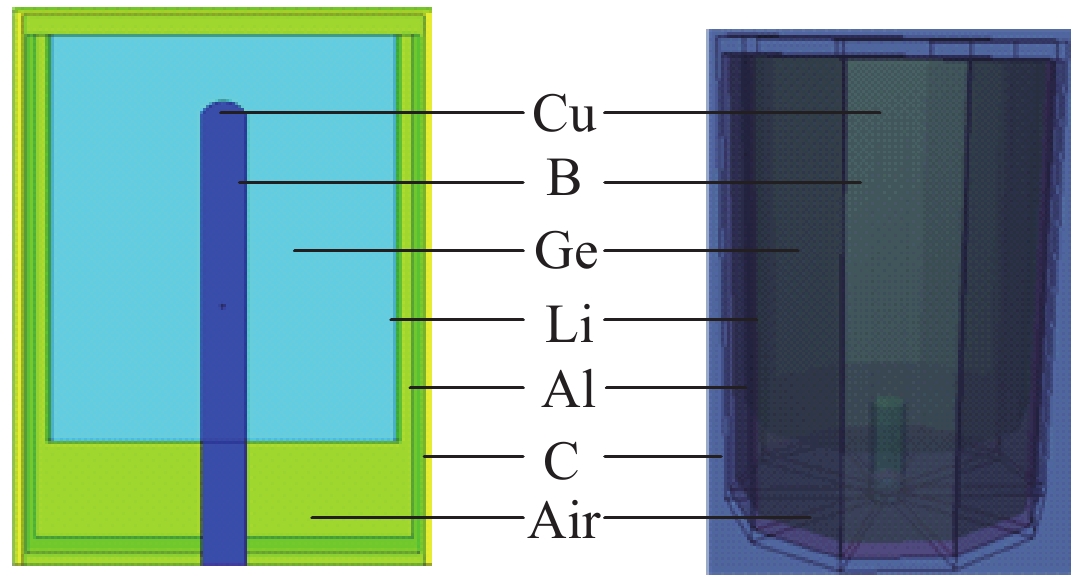
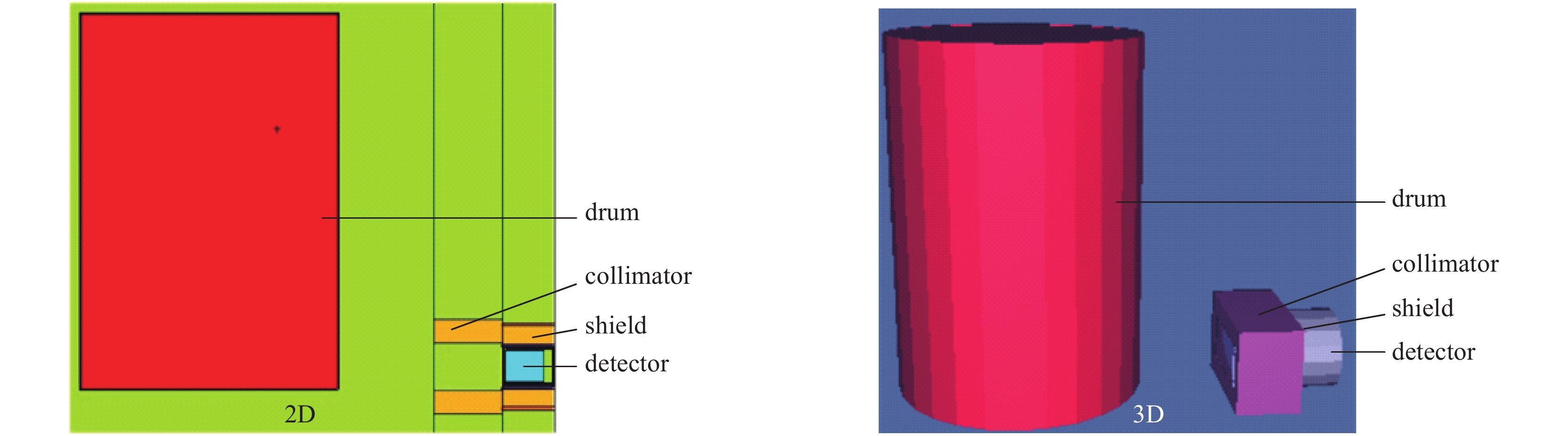
A passive efficiency calibration method with Monte Carlo simulation in segmented gamma scanning
-
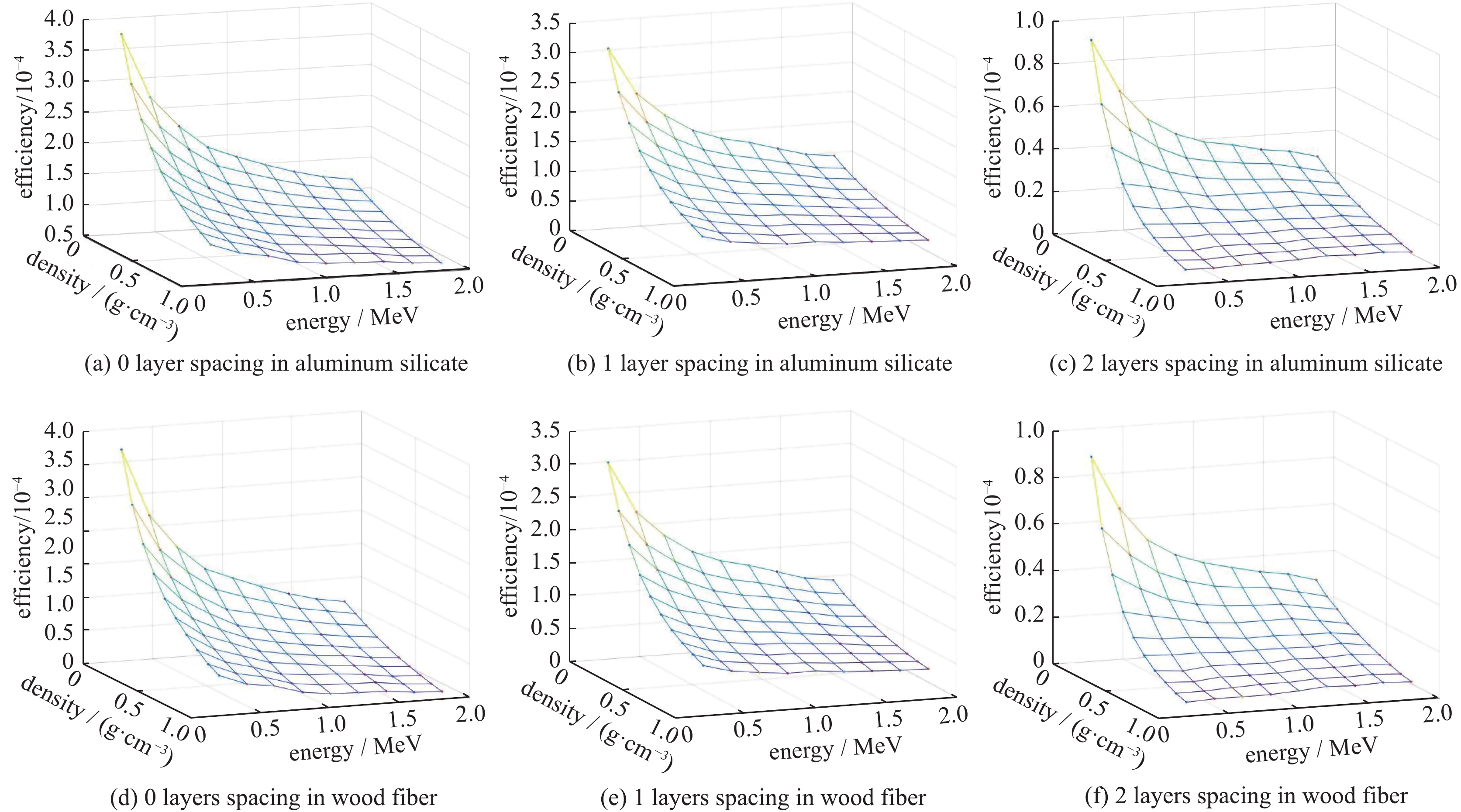
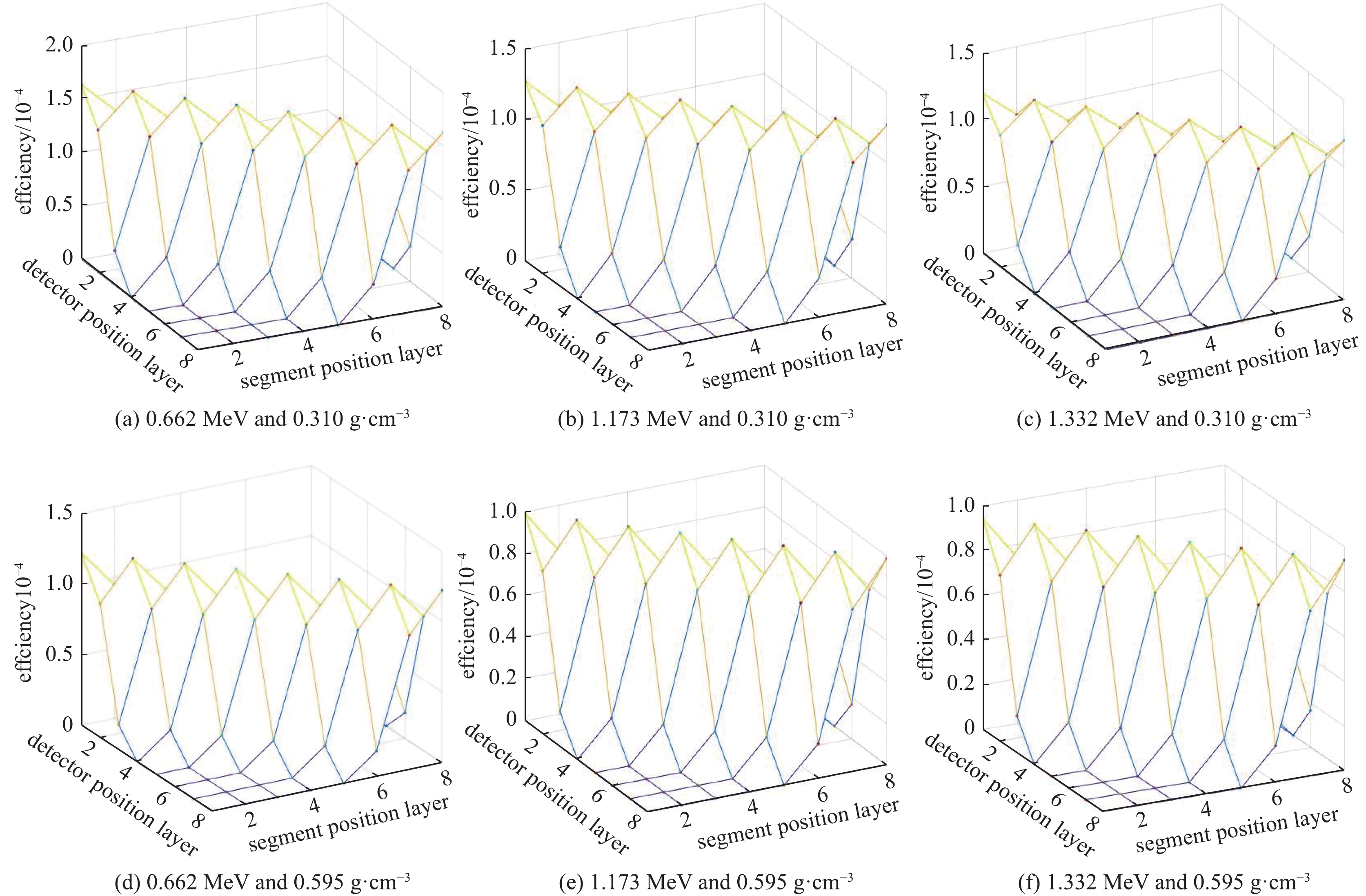
摘要: 针对200 L核废物桶分段γ扫描(SGS)过程中的效率刻度问题,提出了一种效率刻度函数模型,采用MCNP程序计算不同基质密度和γ射线能量条件下的离散断层效率,经过多元非线性回归获取函数参数,从而建立效率刻度函数,实现核废物桶SGS断层效率刻度。对核废物桶样品进行实验分析,结果表明:对于桶内基质分别为密度0.310 g·cm−3的硅酸铝、密度0.595 g·cm−3的木质纤维,桶内核素分别为活度3.110×105 Bq的点源137Cs、活度1.371×105 Bq的点源60Co,在桶内仅有单个点源存在的核素分布极端不均匀情况下,桶内核素活度重建误差在−37.68%~31.52%范围内。本文的方法能够准确有效实现核废物桶SGS断层效率矩阵计算,并确定核废物桶内放射性核素活度,满足实际检测要求。Abstract: In this work, an efficiency calibration function model is presented to calculate the efficiency of segment in segmented gamma scanning (SGS) for 200 L nuclear waste drum. Discrete SGS efficiencies are simulated with MCNP for different densities and gamma ray energies. Parameters of function are determined by using multivariate nonlinear regression method with the efficiencies. The SGS efficiency calibration function is constructed to calculate the efficiency matrix. Aluminum silicate with density of 0.310 g·cm−3, wood fiber of 0.595 g·cm−3, point sources 137Cs with activity of 3.110×105 Bq and 60Co of 1.371×105 Bq are used to construct samples of drum for SGS analysis. Result shows: for the extremely heterogeneous radioisotope distribution of only a point source placed at 8 different positions in the drum, errors of reconstructed activities are −37.68%~31.52%. Overall, the reconstructed activity is in agreement with the true activity. This method effectively and accurately achieves SGS efficiency calculation and reconstruction of activity.
-
Key words:
- nuclear waste drum /
- segmented gamma scanning /
- Monte Carlo /
- efficiency calibration /
- function /
- MLEM algorithm
-
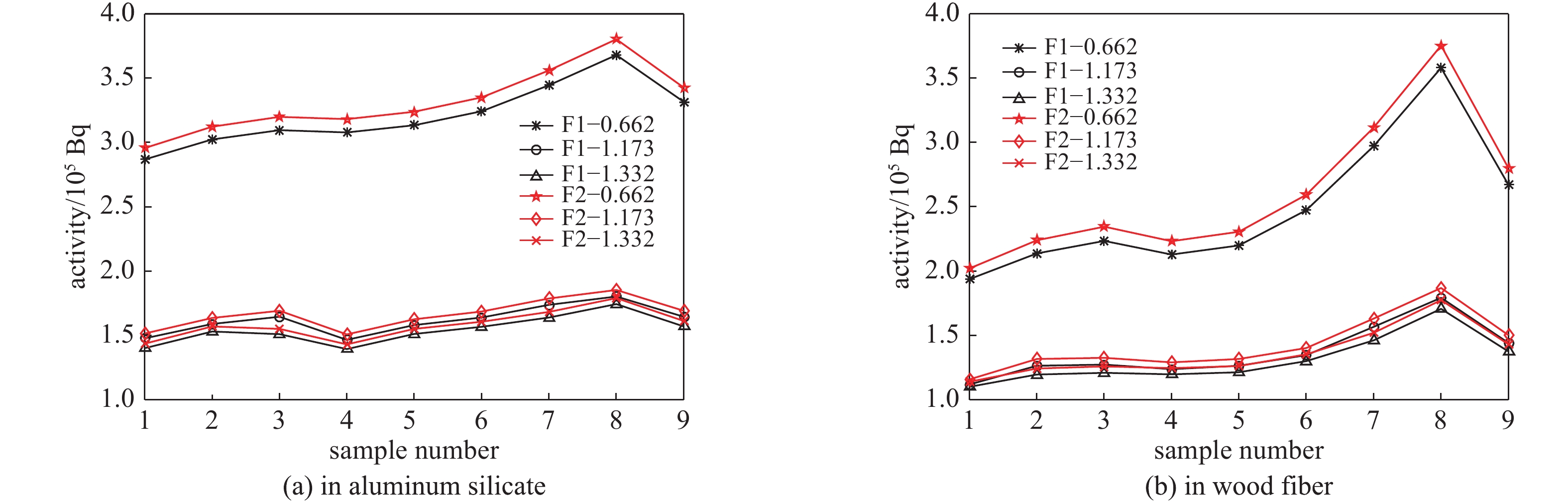
图 8 两种刻度函数参数下活度重建结果对比
Figure 8. Comparison of reconstructed activity with two sets of parameters (F1 and F2 represent parameters calibrated by aluminum silicate and wood fiber respectively, as shown in Table 1)
表 1 效率刻度函数参数
Table 1. Parameters of efficiency function
calibrating material spacing parameter a1 a2 a3 a4 a5 a6 R2 aluminum silicate 0 layer between detector and segment −8.214 −0.322 −0.681 −0.034 0.101 −0.601 0.998 1 layer between detector and segment −8.376 −0.303 −0.870 −0.051 0.110 −0.564 0.998 2 layers between detector and segment −10.094 −0.015 −2.014 −0.014 0.224 0.346 0.996 wood fiber 0 layer between detector and segment −8.152 −0.312 −0.676 −0.031 0.102 −0.713 0.999 1 layer between detector and segment −8.341 −0.293 −0.888 −0.047 0.111 −0.637 0.998 2 layers between detector and segment −10.052 0.011 −2.098 −0.015 0.231 0.276 0.996 表 2 137Cs和60Co核素的重建活度和误差
Table 2. Reconstructed activities and errors of 137Cs and 60Co
samples
No.activity in aluminum silicate/Bq(error/%) activity in wood fiber/Bq 0.662 MeV 1.173 MeV 1.332 MeV 0.662 MeV 1.173 MeV 1.332 MeV 1# 2.869×105(−7.74) 1.479×105(7.89) 1.403×105(2.33) 1.938×105(−37.68) 1.119×105(−18.35) 1.102×105(−19.54) 2# 3.025×105(−2.74) 1.591×105(16.08) 1.532×105(11.77) 2.138×105(−31.25) 1.265×105(−7.68) 1.197×105(−12.6) 3# 3.096×105(−0.46) 1.646×105(20.08) 1.512×105(10.32) 2.235×105(−28.15) 1.273×105(−7.09) 1.211×105(−11.64) 4# 3.079×105(−0.99) 1.468×105(7.07) 1.396×105(1.79) 2.129×105(−31.56) 1.239×105(−9.6) 1.199×105(−12.48) 5# 3.134×105(0.78) 1.582×105(15.39) 1.513×105(10.36) 2.199×105(−29.3) 1.265×105(−7.64) 1.215×105(−11.34) 6# 3.243×105(4.29) 1.640×105(19.61) 1.568×105(14.34) 2.474×105(−20.44) 1.347×105(−1.7) 1.302×105(−4.93) 7# 3.445×105(10.78) 1.739×105(26.81) 1.640×105(19.66) 2.972×105(−4.43) 1.567×105(14.35) 1.463×105(6.81) 8# 3.680×105(18.32) 1.803×105(31.52) 1.745×105(27.24) 3.579×105(15.07) 1.794×105(30.97) 1.708×105(24.65) 9# 3.316×105(6.63) 1.646×105(20.07) 1.572×105(14.68) 2.670×105(14.13) 1.442×105(5.28) 1.377×105(0.54) -
[1] 刘哲, 张丽. γ射线CT放射性废物桶检测技术综述[J]. CT理论与应用研究, 2014, 23(6):1025-1040. (Liu Zhe, Zhang Li. Review of γ-ray CT for radioactive waste assay[J]. CT Theory and Applications, 2014, 23(6): 1025-1040 [2] 张全虎. 层析γ扫描(TGS)重建技术的研究[D]. 北京: 中国原子能科学研究院, 2003.Zhang Quanhu. Research of tomographic gamma scanning (TGS) reconstruction technique[D]. Beijing: China Institute of Atomic Energy, 2003 [3] 莫继锋, 李美山, 张存平, 等. SGS技术在放射性固体废物整备检测中的应用[J]. 核电子学与探测技术, 2014, 34(8):950-953. (Mo Jifeng, Li Meishan, Zhang Cunping, et al. Application on the SGS technology in the measurement of radioactive solid waste conditioning[J]. Nuclear Electronics and Detection Technology, 2014, 34(8): 950-953 doi: 10.3969/j.issn.0258-0934.2014.08.008 [4] 周志波. 桶装核废物快速检测方法研究[D]. 北京: 中国原子能科学研究院, 2007.Zhou Zhibo. Research on the analysis method for the fast measurement of nuclear waste with γ spectrum[D]. Beijing: China Institute of Atomic Energy, 2007 [5] Parker J L. Use of calibration standards and the correction for sample self-attenuation in gamma-ray nondestructive assay[J]. Inorganic Organic Physical & Analytical Chemistry, 1984. [6] Prettyman T H, Reilly T D, Miller M C, et al. Advances in nuclear instrumentation for safeguards[R]. LA-UR-96-3757, 1996 [7] Camp D C, Martz H E, Roberson G P, et al. Nondestructive waste-drum assay for transuranic content by gamma-ray active and passive computed tomography[J]. Nuclear Instruments and Methods in Physics Research A, 2002, 495: 69-83. doi: 10.1016/S0168-9002(02)01315-3 [8] Hsue S T, Stewart J E. Guide to nondestructive assay standard preparation, criteria, availability and practical considerations[R]. La-13340-Ms, 2000. [9] 刘月恒, 屠荆, 仲云红. 环境样品测量中的一种自吸收校正方法研究[C]//全国第5届核仪器及其应用学术会议. 2005.Liu Yueheng, Tu Jing, Zhong Yunhong. A method of self-sorption correction for environmental radioactive measurement[C]//Proceedings of the 5th National Conference on Nuclear Instrument & Its Application. 2005 [10] Bosko A, Geurkov G, Croft S, et al. Advanced approach for calibration of the segmented gamma scanner for the radioassay of drummed waste[C]//2006 IEEE Nuclear Science Symposium Conference Record. 2006: 212-213. [11] Nakazawa D, Bronson F, Croft S, et al. The efficiency calibration of non-destructive gamma assay systems using semi-analytical mathematical approaches[C]//WM2010 Conference. 2010. [12] 易珂. 中低放射性废物活度无源γ测量实验及模拟计算研究[D]. 上海: 上海交通大学, 2009.Yi Ke. Experimental study and simulation of the passive gamma measurement on low-and-intermediate-level radioactive waste[D]. Shanghai: Shanghai Jiao Tong University, 2009 [13] Liang J H, Jiang S H, Chou G T, et al. A theoretical investigation of calibration methods for radwaste radioactivity detection systems[J]. Applied Radiation and Isotopes, 1996, 47(7): 669-675. doi: 10.1016/0969-8043(96)00031-0 [14] Bruggeman M, Gerits J, Carchon R. A minimum biased shell-source method for the calibration of radwaste assay systems[J]. Applied Radiation and Isotopes, 1999, 51(3): 255-259. doi: 10.1016/S0969-8043(99)00041-X [15] 徐利军, 叶宏生, 张卫东, 等. 分段γ扫描装置校准用桶状标准源的设计[J]. 核技术, 2015, 38:050502. (Xu Lijun, Ye Hongsheng, Zhang Weidong, et al. Design of reference radioactive source of waste drum used in calibration of segmented gamma scan device[J]. Nuclear Techniques, 2015, 38: 050502 [16] 许淑艳. 蒙特卡罗方法在实验核物理中的应用[M]. 北京: 原子能出版社, 2006.Xu Shuyan. Application of Monte Carlo method in nuclear physics experiment[M]. Beijing: Atomic Energy Press, 2006 [17] Dung T Q. Calculation of the systematic error and correction factors in gamma waste assay system[J]. Annals of Nuclear Energy, 1997, 24(1): 33-47. doi: 10.1016/0306-4549(96)00059-X -




 下载:
下载: