Simulation and experimental study on high velocity control of armature in bore
-
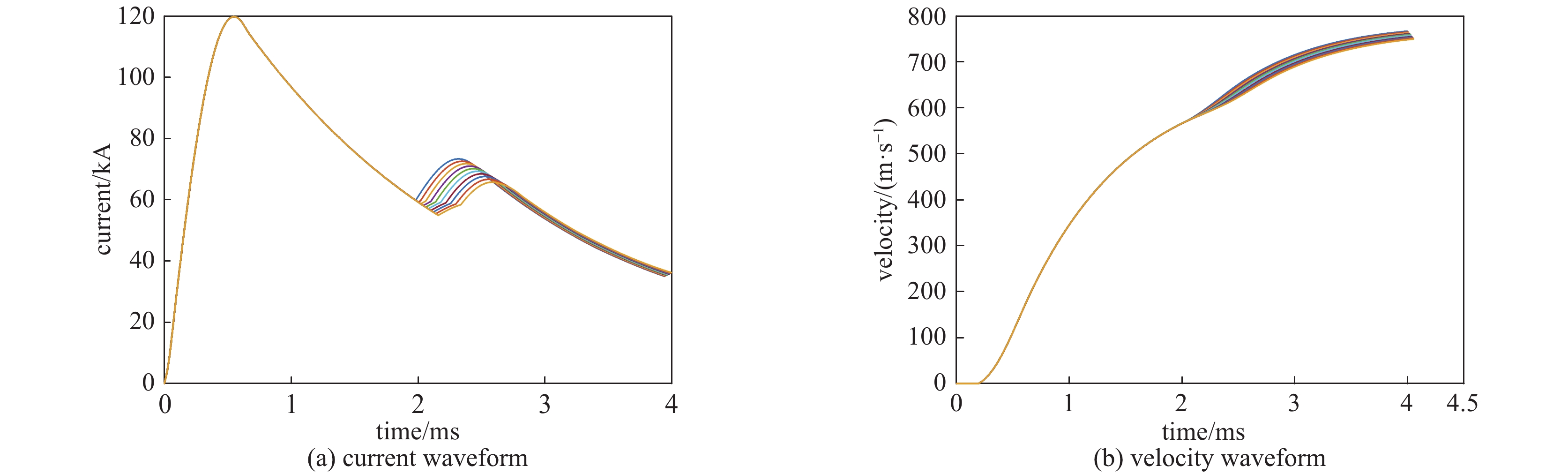
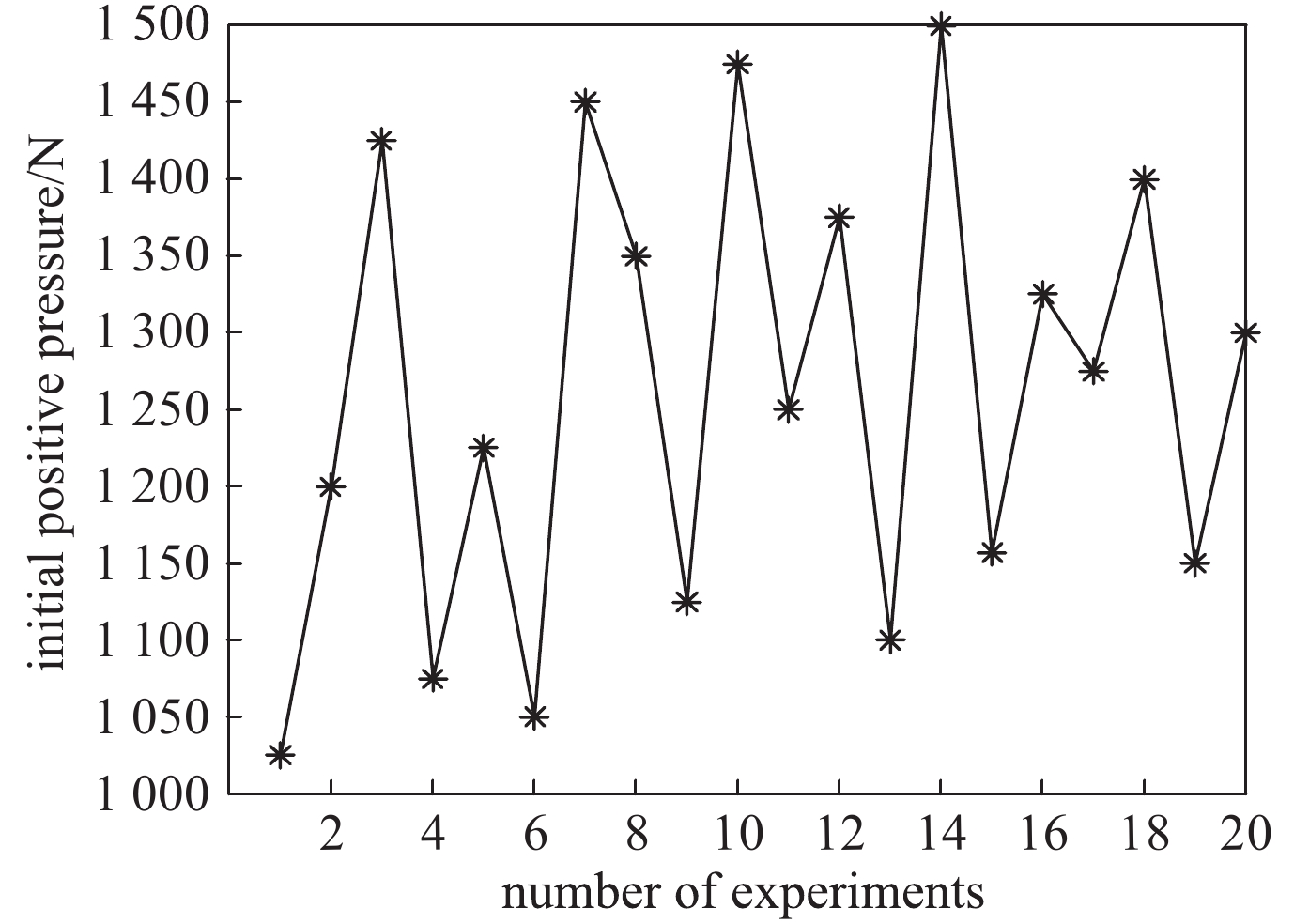
摘要: 电磁轨道发射的过程中,电枢在膛内高速运动时会受到电磁力、电枢初始正压力、摩擦力、空气阻力、烧蚀阻力等多种因素影响,电枢的出口速度呈现出在一定范围内波动的特征。为了提高电枢的出口速度精度,针对膛内电枢与轨道摩擦不均衡性和烧蚀程度不确定的特性,综合考虑脉冲成形网络的电路模型与电枢的动力学特征,建立了电枢在膛内的运动开环控制仿真模型。通过仿真,得出了脉冲电源模块触发时刻与电枢出口速度之间的关系,提出了电枢出口速度闭环控制模型,探究了电枢出口速度控制可行方案。结果表明:应用闭环控制算法,可实现对电枢出口速度的精确控制。Abstract: During the launching of electromagnetic railgun, movement of the armature will be influenced by many factors, such as electromagnetic force, armature initial positive pressure, friction force, air resistance and electrical erosion resistance when the armature is moving in the bore. The muzzle velocity of the armature will fluctuate in a certain range. To improve the precision of the muzzle velocity of the armature, based on the character of the uncertainty of friction and ablation degree of armature and rail, this paper presents a simulation model for the open loop control of the armature in the bore, considering the dynamic characteristics of the circuit model and armature. The relationship between the discharge time interval and muzzle velocity of the armature is obtained by simulation, the armature velocity closed loop control model is put forward, and the feasible scheme of armature velocity control is explored. The simulation results show that the closed-loop control can improve the control precision of the muzzle velocity of the armature.
-
Key words:
- electromagnetic launching /
- mathematical model /
- muzzle velocity /
- velocity control
-
表 1 实验结果
Table 1. Results of experiments
initial positive
pressure/kNtest situation rail length/m charging voltage/kV trigger time of the first
group of modules/μstrigger time of the second
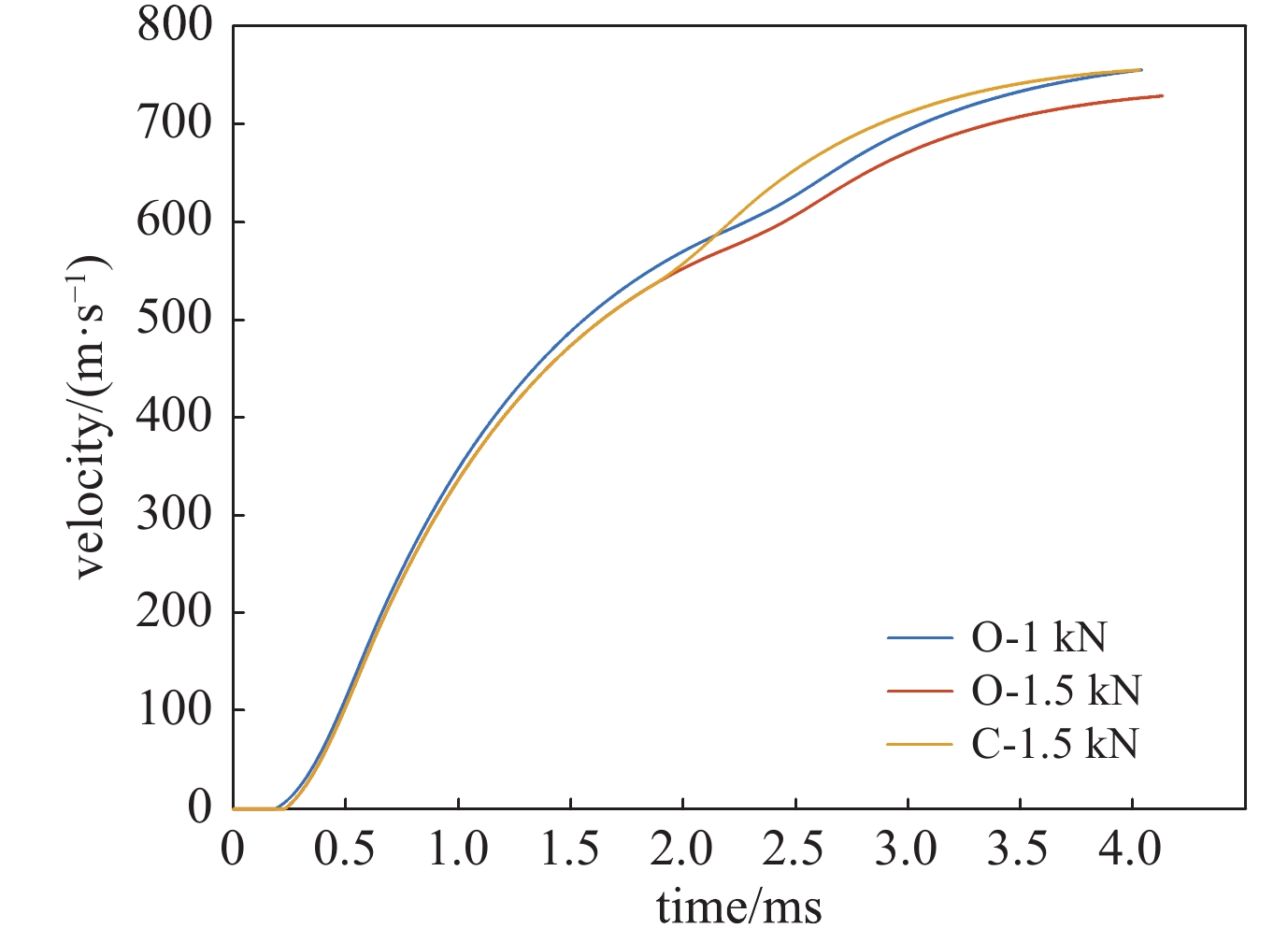
group of modules/ms1.0 open loop control 2 1.5 0 2.3 1.5 open loop control 2 1.5 0 2.3 1.5 closed loop control 2 1.5 0 calculated Ttrig 表 2 开环控制与闭环控制速度误差表
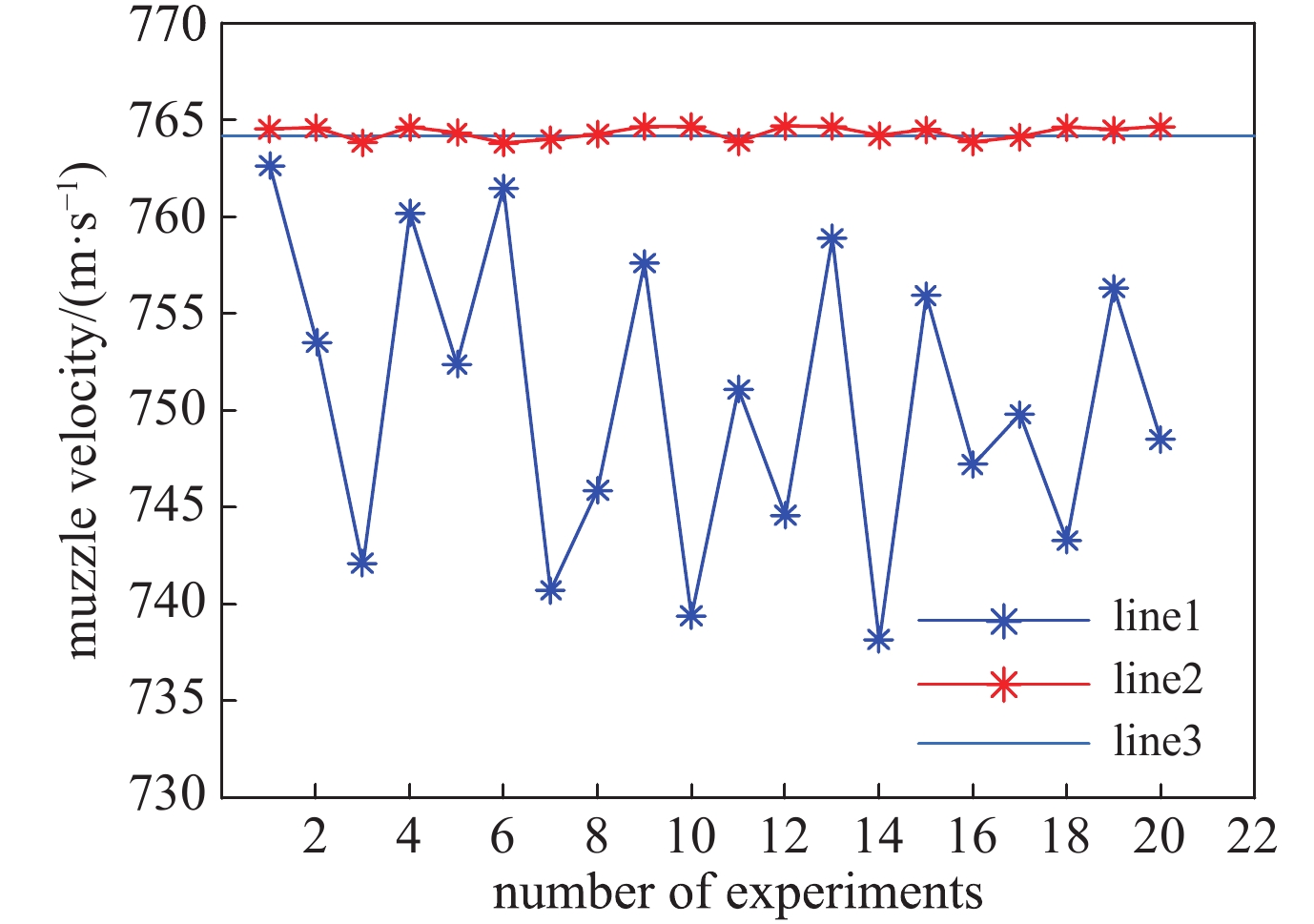
Table 2. Speed error table of open-loop control and closed-loop control
number of experiments open loop simulation muzzle velocity/(m·s−1) simulation relative error/% closed loop simulation muzzle velocity/(m·s−1) simulation relative error/% 1 762.8 −0.188 764.5 0.042 2 753.7 −1.407 764.6 0.054 3 742.0 −2.975 763.8 −0.050 4 760.2 −0.536 764.6 0.055 5 752.4 −1.581 764.3 0.018 6 761.5 −0.362 763.8 −0.054 7 740.7 −3.149 763.9 −0.030 8 745.9 −2.452 764.2 0.006 9 757.6 −0.885 764.6 0.061 10 739.4 −3.324 764.6 0.062 11 751.1 −1.756 763.8 −0.046 12 744.6 −2.627 764.7 0.063 13 758.9 −0.710 764.6 0.061 14 738.1 −3.498 764.2 −0.002 15 755.9 −1.108 764.5 0.040 16 747.2 −2.278 763.8 −0.048 17 749.8 −1.930 764.1 −0.010 18 743.3 −2.800 764.6 0.056 19 756.3 −1.059 764.5 0.039 20 748.5 −2.100 764.6 0.062 -
[1] Li Jun, Li Shizhong, Liu Peizhu, et al. Design and testing of a 10-MJ electromagnetic launch facility[J]. IEEE Trans Plasma Science, 2011, 39(4): 1187-1191. doi: 10.1109/TPS.2011.2110649 [2] Wang Ying, Chen Shukang, Zheng Ping. Widely developing electric launch technology in China[J]. IEEE Trans Magnetics, 2003, 39(1): 39-41. doi: 10.1109/TMAG.2002.805914 [3] 关永超, 邹文康, 何勇, 等. 串联型双轨增强电磁轨道炮电路模拟[J]. 强激光与粒子束, 2014, 26:115001. (Guan Yongchao, Zou Yongkang, He Yong, et al. Circuit simulation of series double rail enhanced electromagnetic railgun[J]. High Power Laser and Particle Beams, 2014, 26: 115001 [4] 赵莹, 徐蓉, 袁伟群, 等. 脉冲大电流电磁轨道发射装置特性[J]. 强激光与粒子束, 2014, 26:095004. (Zhao Ying, Xu Rong, Yuan Weiqun, et al. Characteristics of high current pulse electromagnetic track launcher[J]. High Power Laser and Particle Beams, 2014, 26: 095004 [5] 刘福才, 王世国, 王振春, 等. 电磁发射测量系统的设计与实现[J]. 兵工学报, 2008, 29(10):1256-1261. (Liu Fucai, Wang Shiguo, Wang Zhenchun, et al. Design and realization of an electromagnetic launch measurement system[J]. Acta Armamentarii, 2008, 29(10): 1256-1261 doi: 10.3321/j.issn:1000-1093.2008.10.021 [6] 何勇, 宋盛义, 关永超, 等. 电磁轨道炮高速滑动接触电阻的定量表征[J]. 强激光与粒子束, 2014, 26:045007. (He Yong, Song Shengyi, Guan Yongchao, et al. Quantitative expression of sliding contact resistance between armature and rail in railgun[J]. High Power Laser and Particle Beams, 2014, 26: 045007 [7] 徐伟东, 袁伟群, 陈允, 等. 电磁轨道发射器连续发射的滑动电接触[J]. 强激光与粒子束, 2012, 24(3):668-672. (Xu Weidong, Yuan Weiqun, Chen Yun, et al. Sliding electrical contact performance of electromagnetic launcher system in rapid fire mode[J]. High Power Laser and Particle Beams, 2012, 24(3): 668-672 doi: 10.3788/HPLPB20122403.0668 [8] Stefani F, Parker J V, Watt T. Progress on developing the “magnetic obturator”, a novel railgun armature[J]. IEEE Trans Magnetics, 2003, 39(1): 86-91. doi: 10.1109/TMAG.2002.805889 [9] Fair H D. Progress in electromagnetic launch science and technology[J]. IEEE Trans Magnetics, 2007, 43(1): 93-98. doi: 10.1109/TMAG.2006.887596 [10] Wang Min, Cao Yanjie, Wang Chenxue, et al. Trigger control research of electromagnetic coil launcher based on real-time velocity measurement[J]. IEEE Trans Plasma Science, 2016, 44(5): 885-888. doi: 10.1109/TPS.2016.2535409 [11] Siaenen T, Schneider M G, Loffler M J. Rail gun muzzle velocity control with high accuracy[J]. IEEE Trans Plasma Science, 2011, 39(1): 133-137. doi: 10.1109/TPS.2010.2052072 [12] Batteh J H. Arc-dynamics calculations in the railgun[R]. Georgia: Science Applications, 1983. [13] Batteh J H, Powell J D. Analysis of plasma arcs in arc-driven railgun[J]. IEEE Trans Magnetics, 1984, 20(2): 336-339. doi: 10.1109/TMAG.1984.1063098 [14] Su Zizhou, Guo Wei, Zhang Tao, et al. Design and simulation of a large muzzle kinetic energy railgun[J]. IEEE Trans Plasma Science, 2013, 41(5): 1416-1420. doi: 10.1109/TPS.2013.2251364 [15] 王振春, 鲍志勇, 曹海要, 等. 增强型电磁轨道炮电枢轨道接触特性研究[J]. 兵工学报, 2018, 39(3):451-456. (Wang Zhenchun, BaoZhiyong, Cao Haiyao, et al. Research on contact characteristics of armature and rail in augmented electromagnetic railgun[J]. Acta Armamentarii, 2018, 39(3): 451-456 doi: 10.3969/j.issn.1000-1093.2018.03.005 [16] 靳智, 沈培辉, 刘凯. 电磁轨道炮电枢的运动特性研究[J]. 兵工自动化, 2013(12):1-3, 32. (Jin Zhi, Shen Peihui, Liu Kai. Research on kinetic characteristic of armature of electromagnetic rail gun[J]. Ordnance Industry Automation, 2013(12): 1-3, 32 doi: 10.7690/bgzdh.2013.12.001 [17] 王莹, 肖峰. 电磁炮原理[M]. 北京: 国防工业出版社, 1995: 2-40.Wang Ying, Xiao Feng. Principle of electromagnetic gun[M]. Beijing: National Defense Industry Press, 1995: 2-40 -




 下载:
下载: