Laser beam coherence and divergence angle complex controlling technique
-
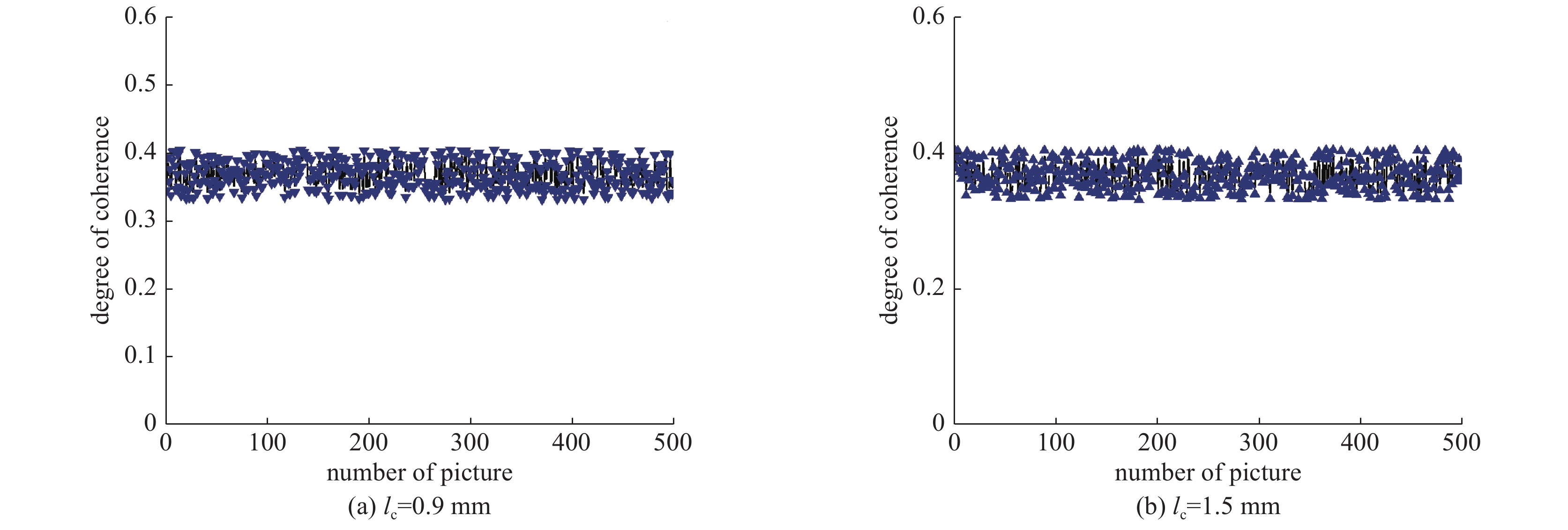
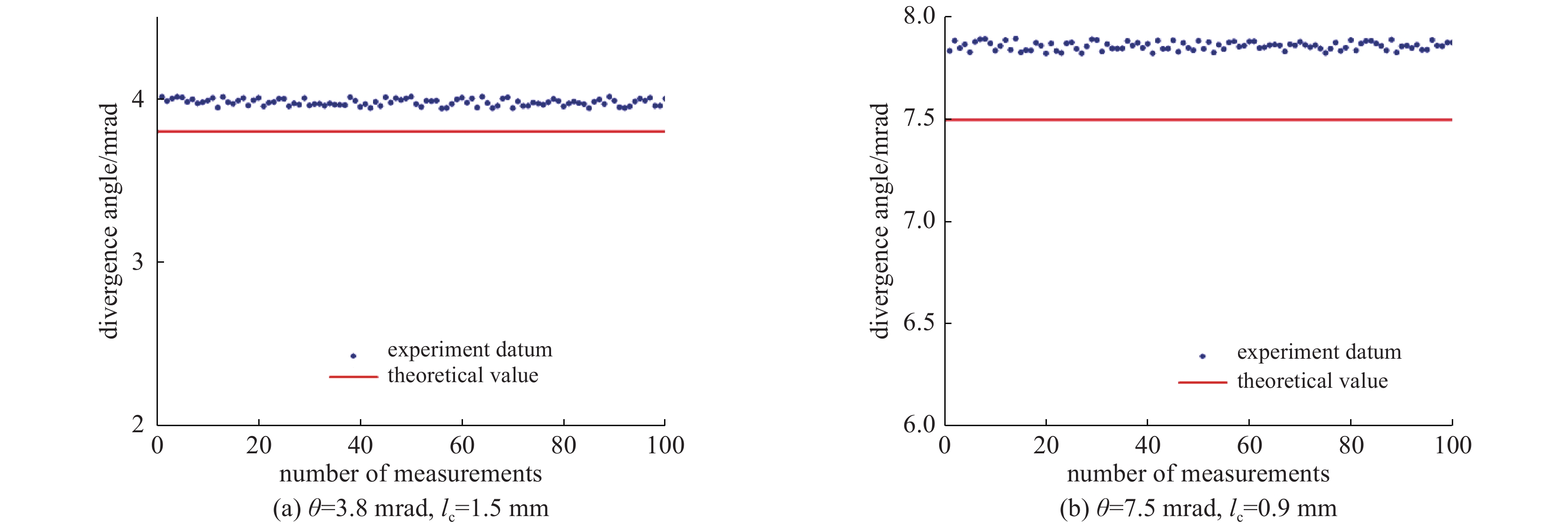
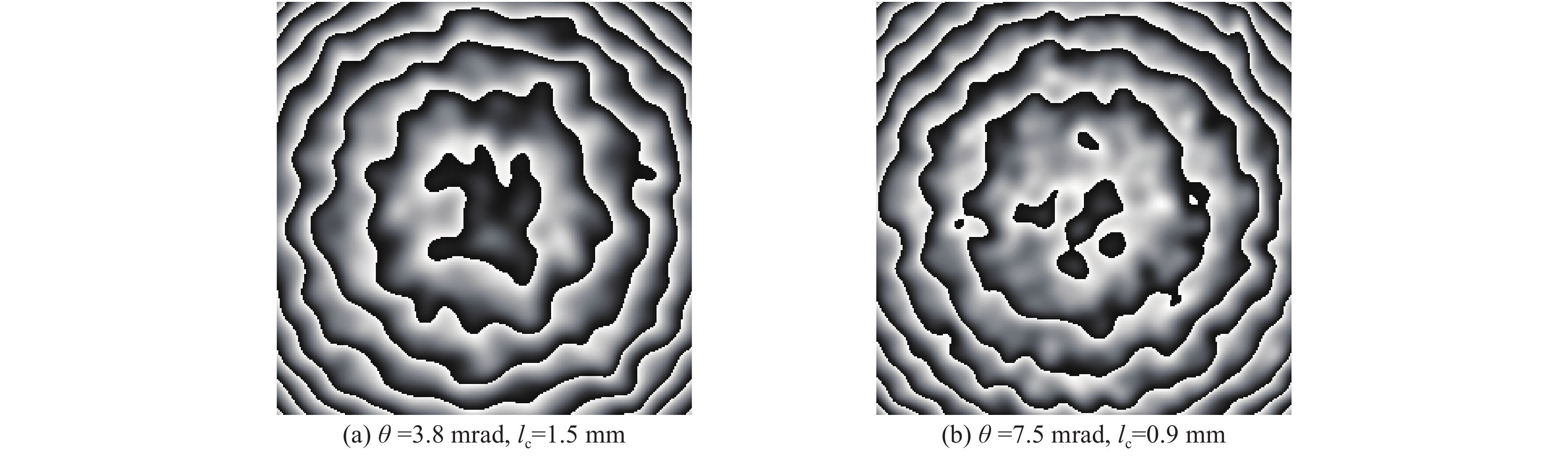
摘要: 为了降低部分相干光光学系统设计的复杂度及成本,增加部分相干光应用的便捷性,提出了一种液晶空间光调制器的激光相干度及束散角复合控制方法。首先介绍了对激光光束进行相干度和束散角复合控制的基本理论和方法;然后分别设置了相干度和束散角检测实验,检测了本方法所调制激光光束的相干度和束散角的准确性。实验结果表明,采用液晶空间光调制器生成相干度为0.9 mm、束散角为7.5 mrad,以及相干度为1.5 mm、束散角为3.8 mrad的部分相干光束,其相干度与理论值相比误差在5%以内,其相干度均方根误差分别为0.027386和0.031314,峰谷值分别为0.084 658和0.089 103;其束散角与理论值相比误差在5%以内,其束散角均方根误差分别为0.022 478和0.023 186,峰谷值分别为0.081 201和0.092 130。可见,该方法可以实现高精度的相干度及束散角复合控制。Abstract: To reduce the complexity and cost of partially coherent optical system, increase the convenience of partially coherent laser beam application, in this paper, we presents a method to control the coherence and divergence angle of laser beam complexly, using a liquid crystal spatial light modulator (LC-SLM). First, we introduce the basic theory and method to control the coherence and divergence angle of laser beam complexly using an LC-SLM; then, we put forward the experiment to test the coherence and divergence angle controlling accuracy. The experiment results show that, for a partially coherent laser beam with the coherence and divergence angle of 0.9 mm, 7.5 mrad and 1.5 mm, 3.8 mrad, the error of coherence is less than 5%, the root-mean-square errors of the degree of coherence are 0.027 386 and 0.031 314, and the peak-to-valley values are 0.084 658 and 0.089 103 respectively; the error of divergence angle is less than 5%, the root-mean-square errors of the divergence angle are 0.022 478 and 0.023 186, and the peak-to-valley values are 0.081 201 and 0.092 130 respectively. This method can control degree of coherence and divergence angle with high accuracy.
-
表 1 双孔参数选择表
Table 1. Selection table of double pinhole
aperture hole spacing/mm d=0.9 mm d=1.5 mm d=0.9 mm d=1.5 mm 0.09 0.015 0.799763 2.221564 0.09 0.16 0.891094 2.527646 0.10 0.17 0.987362 2.853476 0.11 0.18 1.194708 3.199052 0.12 0.20 1.421801 3.949447 0.13 0.25 1.668641 6.171011 0.14 0.30 1.935229 8.886256 0.15 0.35 2.221564 12.09518 0.20 0.40 3.949447 15.79779 0.25 0.45 6.171011 19.99408 -
[1] Korotkova O, Andrews L C, Phillips R L. Speckle propagation through atmospheric turbulence: Effects of a random phase screen at the source[C]//International Symposium on Optical Science and Technology. 2002: 98-109. [2] Korotkova O, Andrews L C, Phillips R L. Model for a partially coherent Gaussian beam in atmospheric turbulence with application in Lasercom[J]. Optical Engineering, 2016, 43(2): 341. [3] Lee I E, Ghassemlooy Z, Ng W P, et al. Joint optimization of partially coherent Gaussian beam for free-space optical communication over turbulent channels with pointing errors[J]. Optics Letters, 2013, 38(3): 350-352. doi: 10.1364/OL.38.000350 [4] Borah D K, Voelz D G. Spatially partially coherent beam parameter optimization for free space optical communications[J]. Opt Express, 2010, 18(20): 20746-20758. doi: 10.1364/OE.18.020746 [5] 柯熙政, 张宇. 部分相干光在大气湍流中的光强闪烁效应[J]. 光学学报, 2015, 35:0106001. (Ke Xizheng, Zhang Yu. Light intensity scintillation effect of partially coherent light in atmospheric turbulence[J]. Acta Photonica Sinica, 2015, 35: 0106001 [6] 李宜璋, 杨晖, 李然, 等. 激光散斑血流成像系统中的光源相干性[J]. 光学 精密工程, 2019, 27(10):2127-2135. (Li Yizhang, Yang Hui, Li Ran, et al. Coherence of light source in laser speckle blood flow imaging system[J]. Optics and Precision Engineering, 2019, 27(10): 2127-2135 doi: 10.3788/OPE.20192710.2127 [7] 柯熙政, 韩美苗, 王明军, 等. 部分相干光在大气湍流中斜程传输路径上的展宽与漂移[J]. 光子学报, 2015, 44:0306001. (Ke Xizheng, Han Meimiao, Wang Mingjun, et al. Spreading and wander of partially coherent beam through atmospheric turbulence in a slanted path[J]. Acta Photonica Sinica, 2015, 44: 0306001 doi: 10.3788/gzxb20154403.0306001 [8] Jenkins M H, Long J M, Gaylord T K. Multifilter phase imaging with partially coherent light[J]. Appl Opt, 2014, 53(16): D29-D39. doi: 10.1364/AO.53.000D29 [9] Deng P, Kavehrad M, Liu Z, et al. Capacity of MIMO free space optical communications using multiple partially coherent beams propagation through non-Kolmogorov strong turbulence[J]. Opt Express, 2013, 21(13): 15213-15229. doi: 10.1364/OE.21.015213 [10] 高明, 刘彦清, 王菲, 等. 偏振部分相干激光波束在湍流大气中传输的扩展和漂移[J]. 光子学报, 2014, 43:1001002. (Gao Ming, Liu Yanqing, Wang Fei, et al. Spread and wander characteristics of polarized and partially coherent laser beam propagated in turbulent atmosphere[J]. Acta Photonica Sinica, 2014, 43: 1001002 doi: 10.3788/gzxb20144310.1001002 [11] Chen Chunyi, Yang Huamin, Zhou Zhou, et al. Effects of source spatial partial coherence on temporal fade statistics of irradiance flux in free-space optical links through atmospheric turbulence[J]. Opt Express, 2013, 24(21): 29731-29743. [12] 倪小龙, 刘智, 姜会林, 等. 采用图形处理器加速的部分相干光实时生成方法[J]. 光子学报, 2016, 45:0310001. (Ni Xiaolong, Liu Zhi, Jiang Huilin, et al. Partially coherent beam real-time generation method accelerated by graphic processing unit[J]. Acta Photonica Sinica, 2016, 45: 0310001 doi: 10.3788/gzxb20164503.0310001 [13] Jennifer C R, Davidson F M. Atmospheric turbulence effects on a partially coherent Gaussian beam: Implications for free-space laser communication[J]. J. Opt Soc Am A, 2002, 19(9): 1794-1801. doi: 10.1364/JOSAA.19.001794 [14] Chen Chunyi, Yang Huamin, Kavehrad M, et al. Validity of quadratic two-source spherical wave structure functions in analysis of beam propagation through generalized atmospheric turbulence[J]. Optics Communications, 2014, 332: 343-349. doi: 10.1016/j.optcom.2014.07.040 [15] Shirai T, Wolf E. Coherence and polarization of electromagnetic beams modulated by random phase screens and their changes on propagation in free space[J]. J Opt Soc Am A, 2004, 21(10): 1907-1916. doi: 10.1364/JOSAA.21.001907 [16] 张洁, 倪小龙, 刘智, 等. 高精度连续变倍率激光扩束系统设计[J]. 中国光学, 2019, 12(3):693-700. (Zhang Jie, Ni Xiaolong, Liu Zhi, et al. Design of high precision continuous variable magnification laser beam expansion system[J]. China Optics, 2019, 12(3): 693-700 doi: 10.3788/co.20191203.0693 [17] 刘春梅. 基于LCOS光学变焦系统研究[D]. 合肥: 安徽大学, 2013. 29-30Liu Chunmei. LCOS-based optical zoom system research[D]. Anhui: Anhui University, 2013, 29-30 [18] 许忠保, 王双迎, 刘文超, 等. 基于液晶空间光调制器的多焦菲涅尔透镜[J]. 光学 精密工程, 2016, 24(10s):156-161. (Xu Zhongbao, Wang Shuangying, Liu Wenchao et al. Multifocal Fresnel lens based on liquid crystal spatial light modulator[J]. Optics and Precision Engineering, 2016, 24(10s): 156-161 [19] 陈浩, 宣丽, 胡立发, 等. 1200 mm望远镜开环液晶自适应光学系统设计[J]. 光学 精密工程, 2010, 18(1):109-117. (Chen Hao, Xuan Li, Hu Lifa, et al. Design of 1200 mm telescope open-loop liquid crystal adaptive optical system[J]. Optics and Precision Engineering, 2010, 18(1): 109-117 [20] Felde C V, Bogatyryova H V, Polyanskii P V, et al. Young's diagnostics of spatial coherence phase singularities[C]//Proc of SPIE. 2014: 62540D. [21] 申琳, 杨进华, 韩福利, 等. 基于光斑图像的激光束散角测量方法研究[J]. 兵工学报, 2011, 32(7):890-895. (Shen Lin, Yang Jinhua, Han Fuli, et al. Research on laser beam divergence angle measurement method based on spot image[J]. Acta Armamentarii, 2011, 32(7): 890-895 -




 下载:
下载: