Suppression of higher diffraction orders using quasiperiodic array of rectangular holes with large size tolerance
-
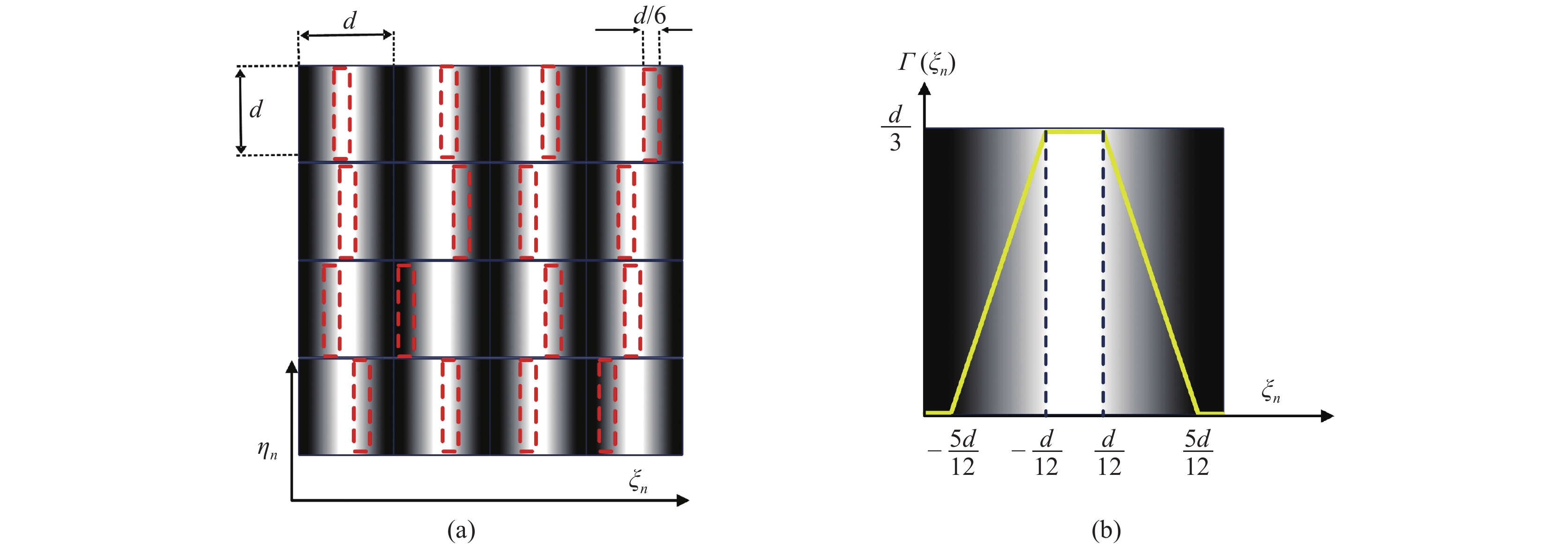
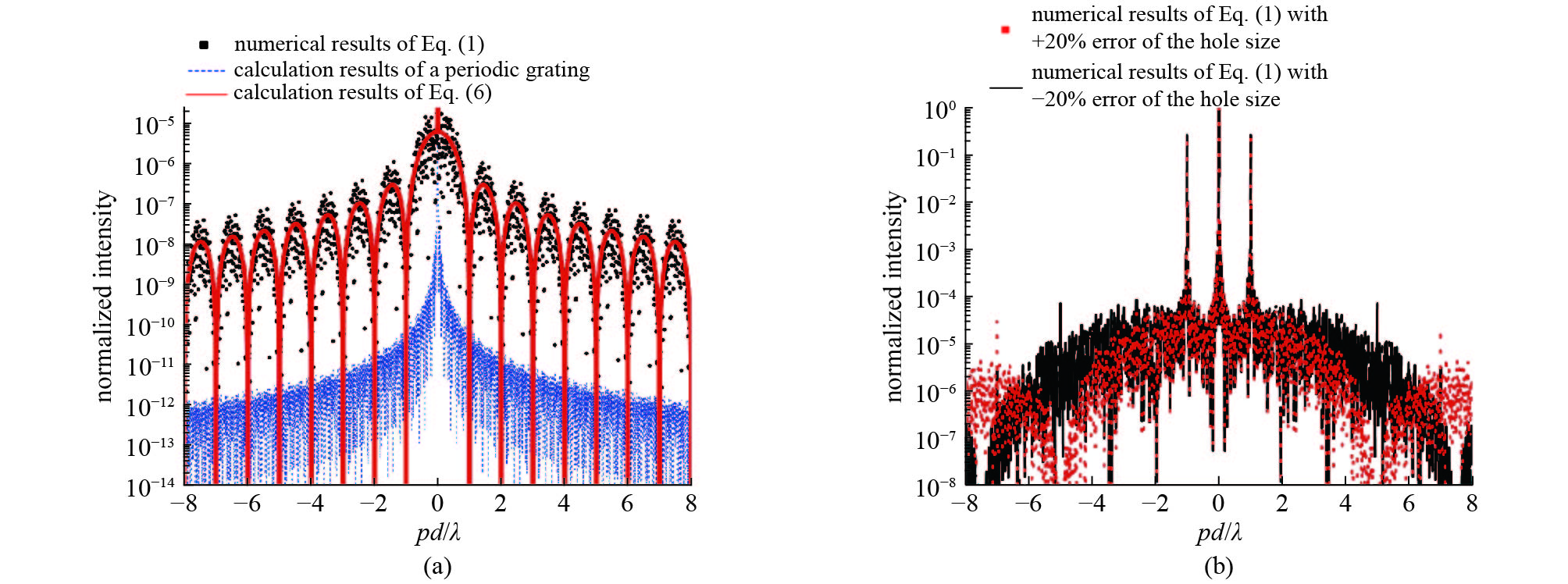
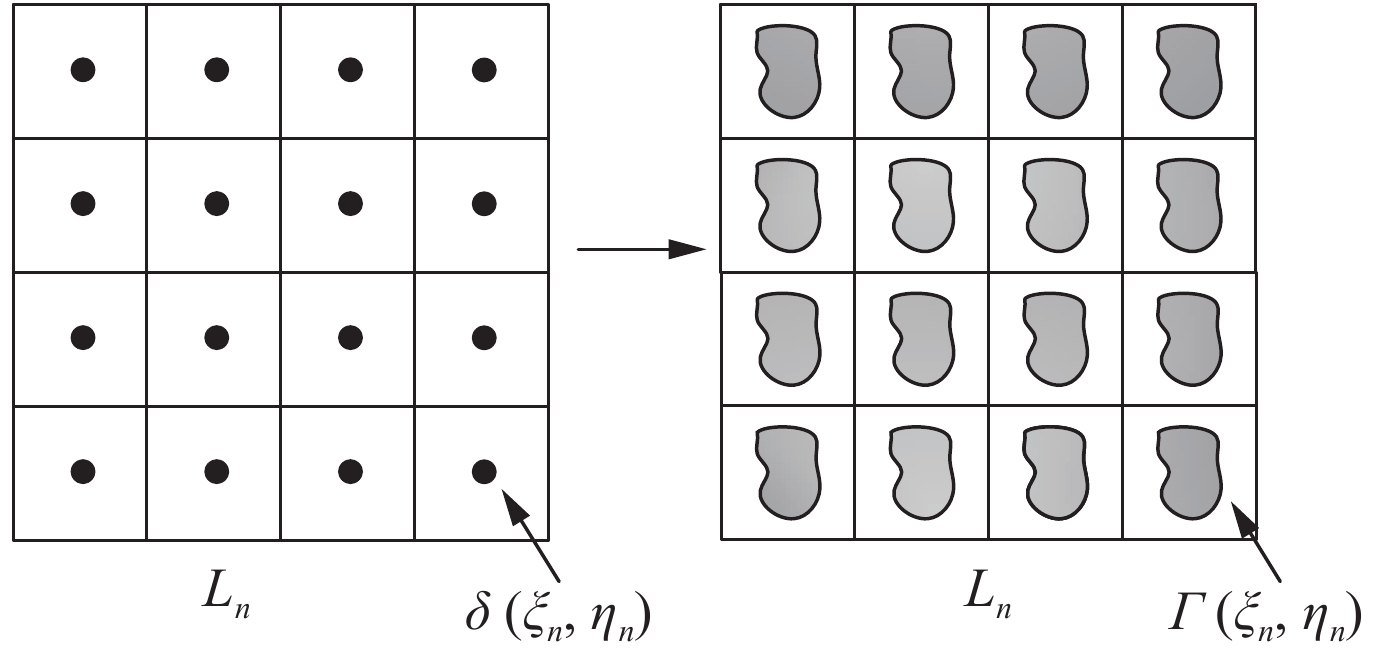
摘要: 传统光栅的基础研究和应用研究进展一直备受关注。然而,高阶衍射污染使传统光栅获得的光谱纯度受到严重影响。为了抑制高阶衍射贡献,人们提出了许多单级或准单级光栅的设计方案,但它们对高阶衍射的抑制效果不可避免地受到加工精度的限制。提出了一种准周期矩形孔阵列光栅,通过优化矩形孔的概率密度分布函数,获得了比以往设计更大的加工误差宽容度。对这种光栅的衍射特性进行了分析研究。理论计算表明,即使孔径相对误差超过20%,光栅也可以完全抑制二阶、三阶和四阶衍射,五阶衍射效率与一阶衍射效率之比小于0.01%,大大降低了对加工精度的要求。Abstract: Advances in basic and applied research of conventional grating have been attracting much attention from optical engineering community. However, the higher orders diffraction contamination degrades the spectral purity obtained by conventional gratings seriously. Many designs of single-order or quasi-single-order gratings have been proposed to suppress higher-order diffraction contributions, however, their inhibitive effects on the higher order diffractions are restrained by the processing accuracy unavoidably. In this paper, we propose a grating that incorporates a quasi-periodical array of rectangular holes, and achieves larger tolerance of processing errors compared with the previously designed gratings by optimizing the probability density distribution function of the holes. This paper describes an analytical study of the diffraction property of this grating. Theoretical calculations reveal that the grating completely suppresses the 2nd, 3rd, and 4th orders diffractions, and the ratio of the 5th order diffraction efficiency to that of the 1st is as low as 0.01% even if relative errors for hole sizes exceed 20%, which greatly decreases the required processing accuracy.
-
Key words:
- single-order diffraction grating /
- X-ray /
- spectrometer /
- tolerance of processing errors
-
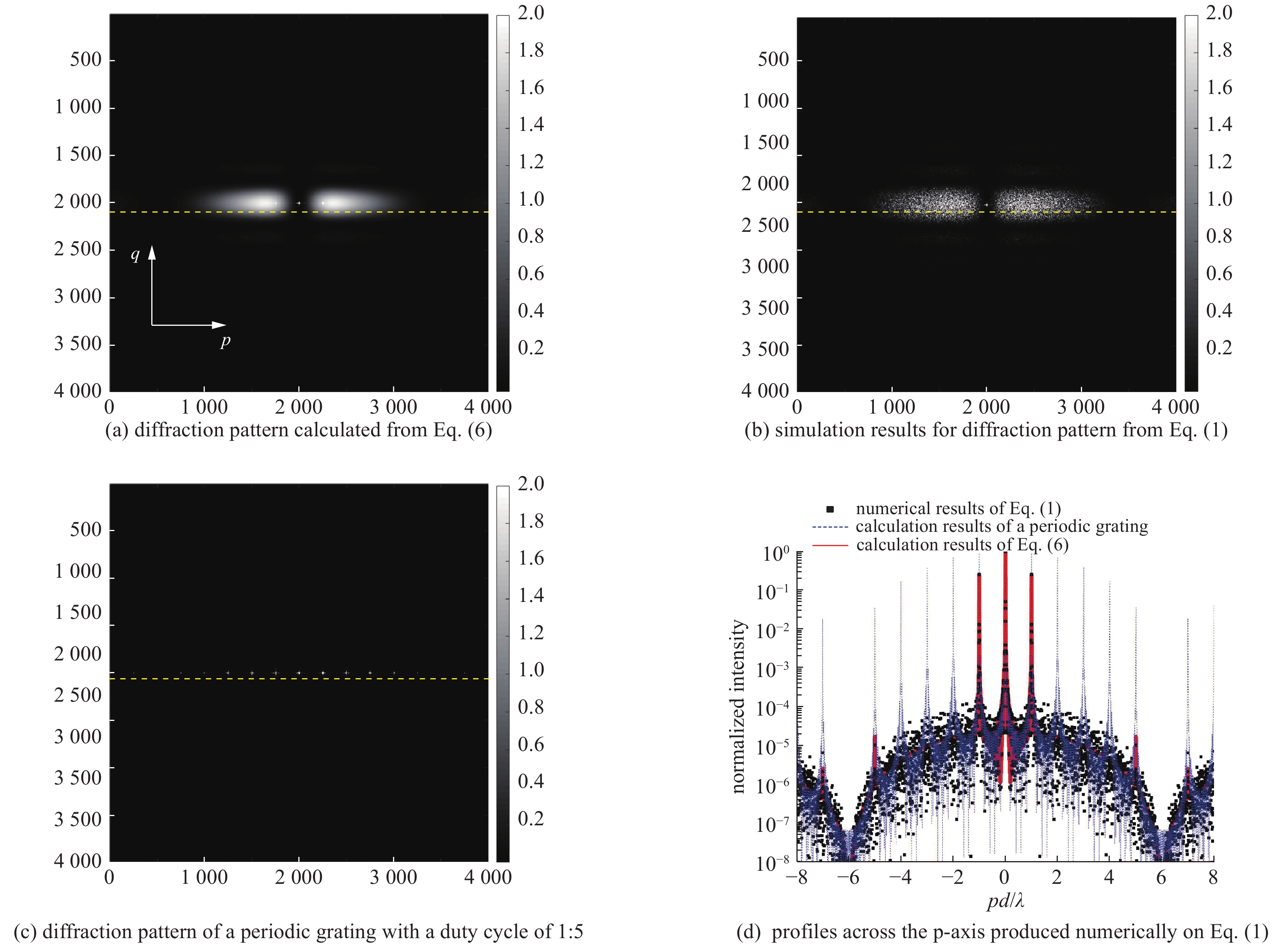
Figure 3. Comparison between far-field diffraction patterns of a quasi-periodical array shown in Fig. 2 when H=L=100 and a periodic grating with a duty cycle of 1∶5 and 201 periods
-
[1] Kallman T, Evans D A, Marshall H, et al. A census of X-ray gas in NGC 1068: Results from 450 ks of Chandra high energy transmission grating observations[J]. Astrophys J, 2014, 780: 121. [2] Wang Q D, Nowak M A, Markoff S B, et al. Dissecting X-ray emitting gas around the center of our galaxy[J]. Science, 2013, 341(30): 981-983. [3] Tzanavaris P, Yaqoob T. New constraints on the geometry and kinematics of matter surrounding the accretion flow in X-ray binaries from Chandra high-energy transmission grating X-ray spectroscopy[J]. Astrophys J, 2018, 855: 25. doi: 10.3847/1538-4357/aaaab6 [4] Shpilman Z, Hurvitz G, Danon L, et al. A combined sinusoidal transmission grating spectrometer and X-ray diode array diagnostics for time-resolved spectral measurements in laser plasma experiments[J]. Rev Sci Instrum, 2019, 90: 013501. doi: 10.1063/1.5051486 [5] Kühne M, Müller P. Higher order contributions in the synchrotron radiation spectrum of a toroidal grating monochromator determined by the use of a transmission grating[J]. Rev Sci Instrum, 1989, 60: 2101. doi: 10.1063/1.1140836 [6] Sokolov A A, Eggenstein F, Erko A, et al. An XUV optics beamline at BESSY II [C]//Proc of SPIE. 2014: 92060J. [7] Suits A G, Heimann P, Yang Xueming, et al. A differentially pumped harmonic filter on the chemical dynamics beamline at Advanced Light Source[J]. Rev Sci Instrum, 1995, 66: 4841. doi: 10.1063/1.1146161 [8] Heimann P A, Koike M, Hsu C W, et al. Performance of the vacuum ultraviolet high-resolution and high-flux beamline for chemical dynamics studies at the Advanced Light Source[J]. Rev Sci Instrum, 1997, 68: 1945. doi: 10.1063/1.1148082 [9] Zhou Hongjun, Wang Guanjun, Zheng Jinjin, et al. Higher order harmonics contribution and suppression in metrology beamline [C]//Proc of SPIE. 2010: 75445 [10] Cao Leifeng, Förster E, Fuhrmann A, et al. Single order X-ray diffraction with binary sinusoidal transmission grating[J]. Appl Phys Lett, 2007, 90: 053501. doi: 10.1063/1.2435618 [11] Zang Huaping, Wang Chuanke, Cao Leifeng, et al. Elimination of higher-order diffraction using zigzag transmission grating in soft X-ray region[J]. Appl Phys Lett, 2012, 100: 111904. doi: 10.1063/1.3693395 [12] Liu Yuwei, Zhu Xiaoli, Gao Yulin, et al. Quasi suppression of higher-order diffractions with inclined rectangular apertures gratings[J]. Sci Rep, 2015, 5: 16502. doi: 10.1038/srep16502 [13] Fan Quanping, Liu Yuwei, Wang Chuanke, et al. Single-order diffraction grating designed by trapezoidal transmission function[J]. Opt Letts, 2015, 40: 2657. doi: 10.1364/OL.40.002657 [14] Liu Ziwei, Shi Lina, Pu Tanchao, et al. Two-dimensional gratings of hexagonal holes for high order diffraction suppression[J]. Opt Express, 2017, 25(2): 1339. doi: 10.1364/OE.25.001339 [15] Kuang Longyu, Wang Chuanke, Wang Zhebin, et al. Quantum-dot-array diffraction grating with single order diffraction property for soft X-ray region[J]. Rev Sci Instrum, 2010, 81: 073508. doi: 10.1063/1.3464197 [16] Li Hailiang, Shi Lina, Wei Lai, et al. Higher-order diffraction suppression of free-standing quasiperiodic nanohole arrays in the X-ray region[J]. Appl Phys Lett, 2017, 110: 041104. doi: 10.1063/1.4974940 [17] Gao Yulin, Zhou Weimin, Wei Lai, et al. Diagnosis of the soft X-ray spectrum emitted by laser-plasmas using a spectroscopic photon sieve[J]. Laser & Particle Beams, 2012, 30(2): 313-317. [18] Chen Yong, Wei Lai, Qian Feng, et al. Higher order harmonics suppression in extreme ultraviolet and soft X-ray[J]. Chin Phys B, 2018, 27: 024101. doi: 10.1088/1674-1056/27/2/024101 [19] Wei Lai, Qian Feng, Yang Zuhua, et al. Diffraction properties of quasi-random pinhole arrays: suppression of higher orders and background fluctuations[J]. J Mod Opt, 2017, 64(21): 2420. doi: 10.1080/09500340.2017.1367853 [20] Wei Lai, Chen Yong, Wang Shaoyi, et al. Suppression of higher diffraction orders in the extreme ultraviolet range by a reflective quasi-random square nano-pillar array[J]. Rev Sci Instrum, 2018, 89: 093110. doi: 10.1063/1.5034764 [21] Hua Y L, Gao N, Xie C Q. Fabrication of ultralarge single order diffraction grating for soft X-ray monochromator [C]//IEEE Symposium on Design, Test, Integration and Packaging of MEMS / MOEMS. 2016: 1–4. -





 下载:
下载: