Validation of a nuclear code system for prismatic high temperature gas-cooled reactors based on the Very High Temperature Reactor Critical Assembly benchmark
-
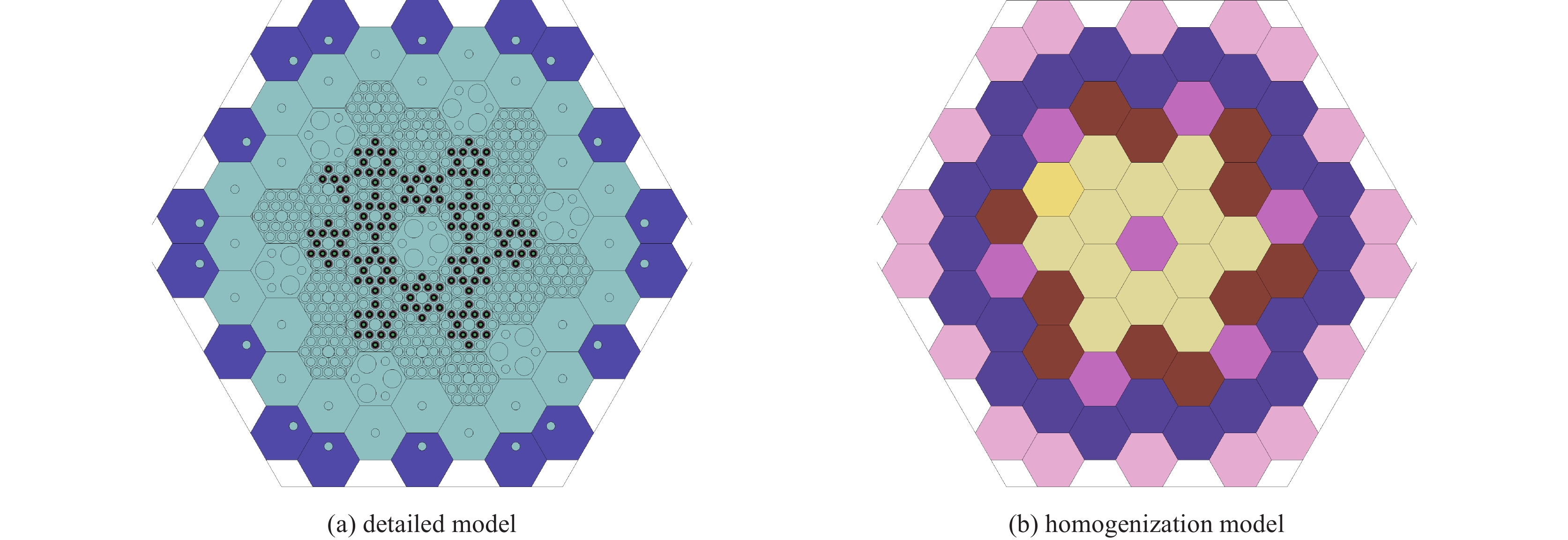
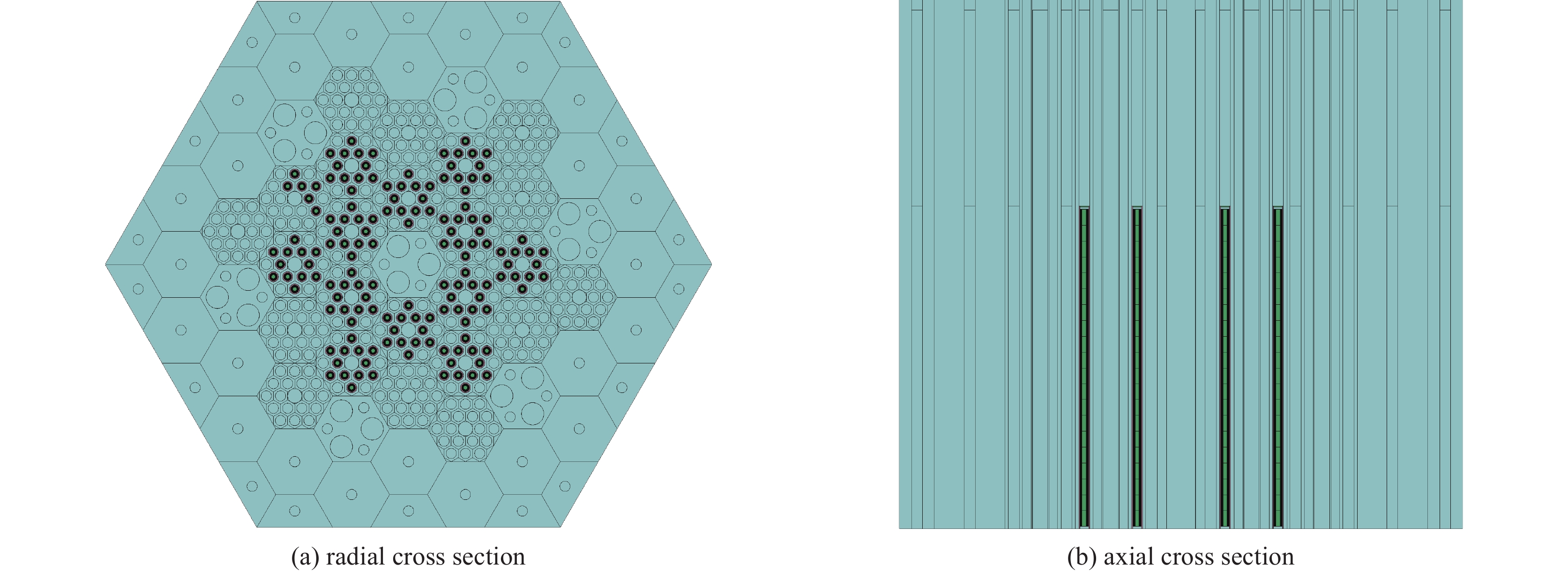
摘要: 高温气冷堆是国际公认的固有安全性高的反应堆堆型。针对高温气冷堆包覆颗粒燃料引入的燃料组件的双重非均匀性以及棱柱式堆芯布置的非均匀性和强空间耦合效应,提出基于蒙特卡罗均匀化-确定论输运方法的RMC-SaraGR程序系统作为棱柱式高温气冷堆的核设计程序。基于日本棱柱式高温气冷堆临界实验装置VHTRC基准题,针对此套核设计程序系统开展了均匀化模型研究和初步验证。研究结果表明,基于蒙特卡罗均匀化方法,采用全堆模型、合适的能群结构和分区方式产生组件群常数,并经过超级等效均匀化方法进行等效均匀化修正,可以保证堆芯多群均匀计算具有较高的计算精度。Abstract: The inherent safety characteristic of high temperature gas-cooled reactor (HTGR) is universally acknowledged. On account of the double-heterogeneity of the coated fuel and the irregular core pattern of the prismatic HTGR, a code system based on Monte-Carlo homogenization and deterministic transport concept was used as a nuclear design code system for prismatic HTGR. An investigation on homogenization model and preliminary validation of this code system is conducted based on VHTRC benchmark which is a prismatic HTGR criticality assembly. The validation results indicate that group constants generation based on Monte-Carlo homogenization and appropriate energy group, then modified by super homogenization (SPH) method further, ensures high precision of homogeneous core calculation.
-
表 1 调整截断石墨组件密度下的keff结果
Table 1. keff results of different density adjustment cases
density adjustment factor keff standard deviation $\Delta {k}_{ {\rm{eff} }\text{} }$/10−5 original 1.00871 0.00026 0 0.5 1.00765 0.00027 −106 0.6 1.00877 0.00024 6 0.65 1.01031 0.00024 160 表 2 不同能群结构下的keff
Table 2. keff of different energy group structure cases
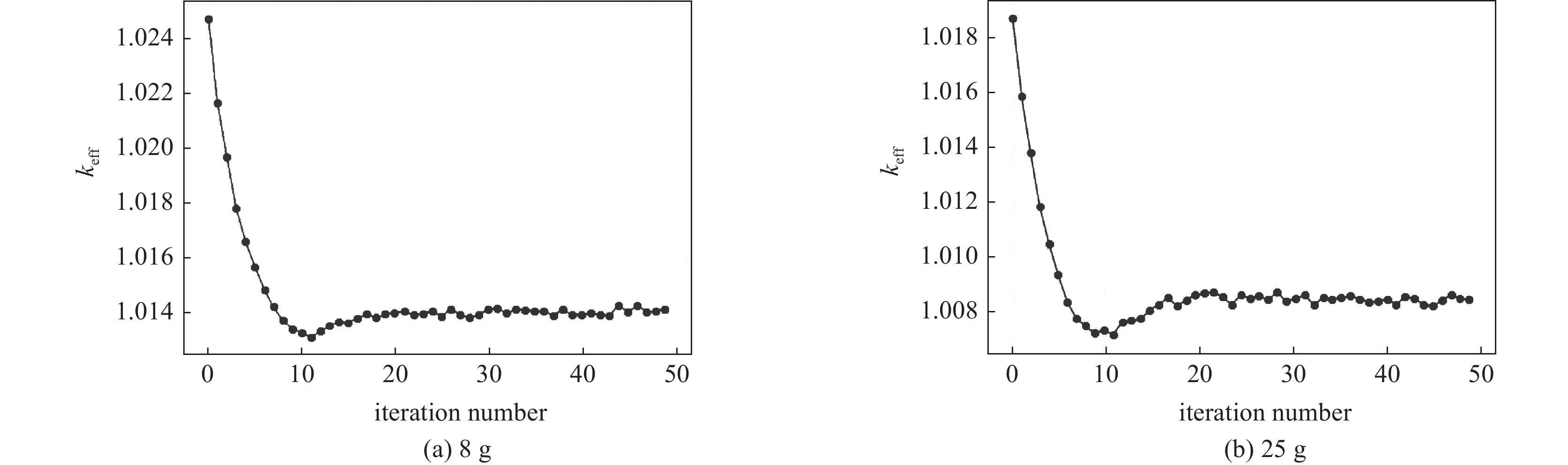
case keff standard deviation $\Delta {k}_{{\rm{eff}}}$/10−5 CE 1.00927 0.00011 MG-4g 1.02818 0.00009 1891 MG-8g 1.02476 0.00011 1549 MG-16g 1.02391 0.00011 1464 MG-25g 1.01844 0.00010 917 MG-40g 1.01786 0.00011 859 MG-70g 1.01661 0.00009 734 表 3 不同分区下功率分布偏差
Table 3. Power discrepancy of different zoning cases
No. relative error/% case 1 case 2 1 0.09 0.10 2 −0.53 −0.54 3 1.40 0.08 4 0.09 0.47 5 −0.20 −0.04 6 0.52 0.38 7 −0.34 −0.05 8 −0.34 −0.12 9 0.18 0.07 10 −0.38 −0.18 11 −0.48 −0.33 12 0.20 0.12 13 0.19 0.16 表 4 不同分区下的keff
Table 4. keff
of different zoning cases keff standard deviation case 1 1.00843 0.00010 case 2 1.00951 0.00008 表 5 不同温度下keff
Table 5. keff of different temperature cases
T/K keff benchmark MVP-II RMC-CE SaraGR 298.65 1.0115±0.0032 1.00706±0.00006 1.00927±0.00011 1.00981 344.35 1.0046±0.0033 0.99998±0.00006 1.00263±0.00010 1.00219 374.05 0.9994±0.0035 0.99527±0.00006 0.99778±0.00011 0.99713 423.65 0.9906±0.0035 0.98700±0.00006 0.98925±0.00010 0.98823 472.75 0.9820±0.0037 0.97893±0.00006 0.98140±0.00011 0.97957 表 6 截面插值计算结果
Table 6. Results with interpolation of cross sections
T/K keff $\Delta {k}_{{\rm{eff}}}$/(10−5) RMC-CE SaraGR-Interp 298.65 1.00927±0.00011 1.00982 55 344.35 1.00263±0.00010 1.00138 −125 374.05 0.99778±0.00011 0.99642 −136 400.00 0.99321±0.00011 0.99234 −87 423.65 0.98925±0.00010 0.98787 −138 472.75 0.98140±0.00011 0.97930 −210 500.00 0.97677±0.00011 0.97491 −186 表 7 等温温度系数
Table 7. Isothermal reactivity coefficient
case $ {\mathrm{\alpha }}_{\mathrm{T}} $/(10−5·K−1) benchmark −17.1 MVP-II −16.4 RMC-CE −16.2 SaraGR −17.6 SaraGR-Interp −17.7 -
[1] 吴宗鑫, 张作义. 先进核能系统和高温气冷堆[M]. 北京: 清华大学出版社, 2004Wu Zongxin, Zhang Zuoyi. The advanced nuclear energy system and high temperature gas-cooled reactor. Beijing: Tsinghua University Press, 2004 [2] 张竞宇, 李富, 孙玉良. 球床高温气冷堆初装载堆芯的物理计算方法及验证[J]. 清华大学学报(自然科学版), 2017, 57(4):405-409. (Zhang Jingyu, Li Fu, Sun Yuliang. Neutronics calculation methods for the first core of the pebble bed high temperature gas cooled reactor[J]. Journal of Tsinghua University (Science and Technology), 2017, 57(4): 405-409 [3] Tsuyoshi Y, Yasunori K, Yuta E. Temperature effect on reactivity in VHTRC-1 core[R]. VHTRC-GCR-EXP-001, 2006. [4] Wang K, Li Z G, She D, et al. RMC – A Monte Carlo code for reactor core analysis[J]. Annals of Nuclear Energy, 2015, 82: 121-129. doi: 10.1016/j.anucene.2014.08.048 [5] 吴高晨. 基于RMC的连续能量蒙特卡罗均匀化与群常数产生[D]. 北京: 清华大学, 2018Wu Gaochen. Research on continuous energy Monte Carlo homogenization and group constant generation based on RMC[D]. Beijing: Tsinghua University, 2018 [6] Yuan Y, Xing J, Huo X D, et al. Research on the on-the-fly homogenization method based on RMC code for criticality calculations[J]. Annals of Nuclear Energy, 2020, 135: 106985. doi: 10.1016/j.anucene.2019.106985 [7] Liu S, She D, Liang J G, et al. Development of random geometry capability in RMC code for stochastic media analysis[J]. Annals of Nuclear Energy, 2015, 85: 903-908. doi: 10.1016/j.anucene.2015.07.008 [8] 卢皓亮, 吴宏春, 曹良志, 等. 中子输运方程的三角形节块SN方法研究[J]. 核动力工程, 2006, 27(5):6-11. (Lu Haoliang, Wu Hongchun, Cao Liangzhi, et al. Nodal SN method for neutron transport equation in triangular geometry[J]. Nuclear Power Engineering, 2006, 27(5): 6-11 doi: 10.3969/j.issn.0258-0926.2006.05.002 [9] Joel D R. CASMO-5: a fuel assembly burnup program user’s manual[R]. SSP-07/431 Rev 9, 2015. -




 下载:
下载: