2.5-D discontinuous Galerkin time-domain method for Maxwell equations
-
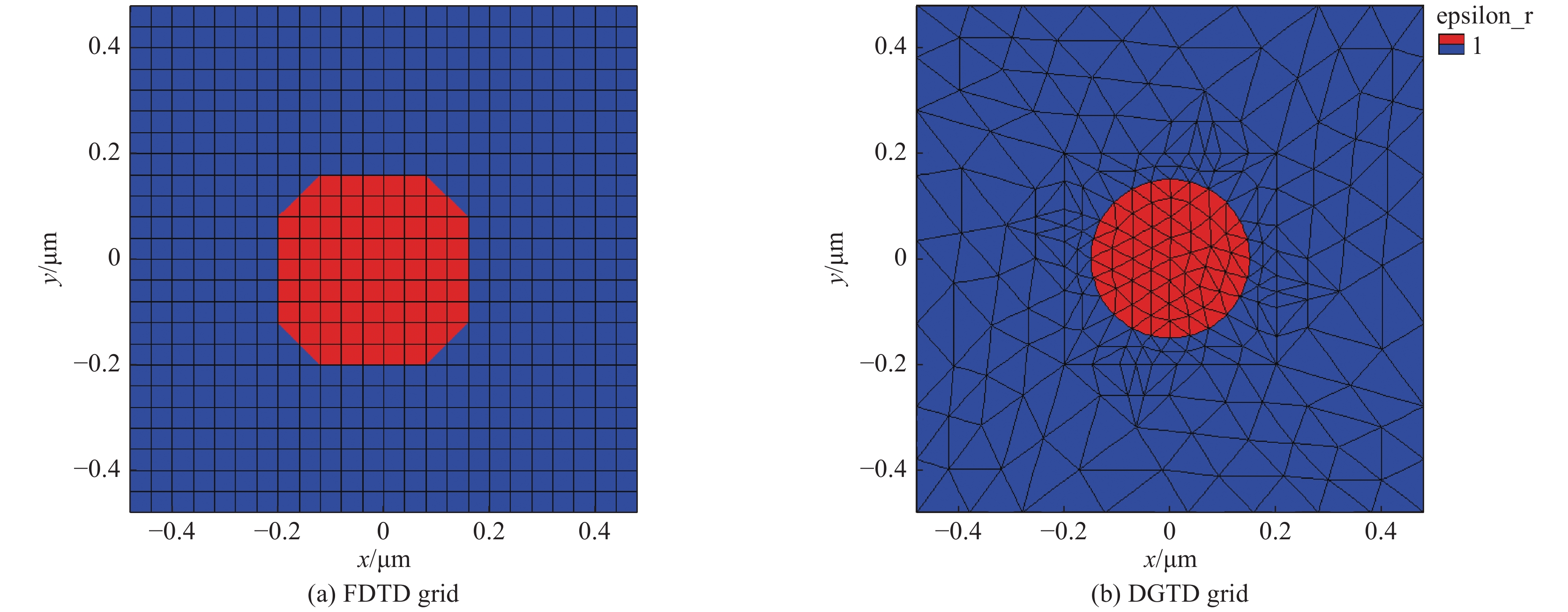
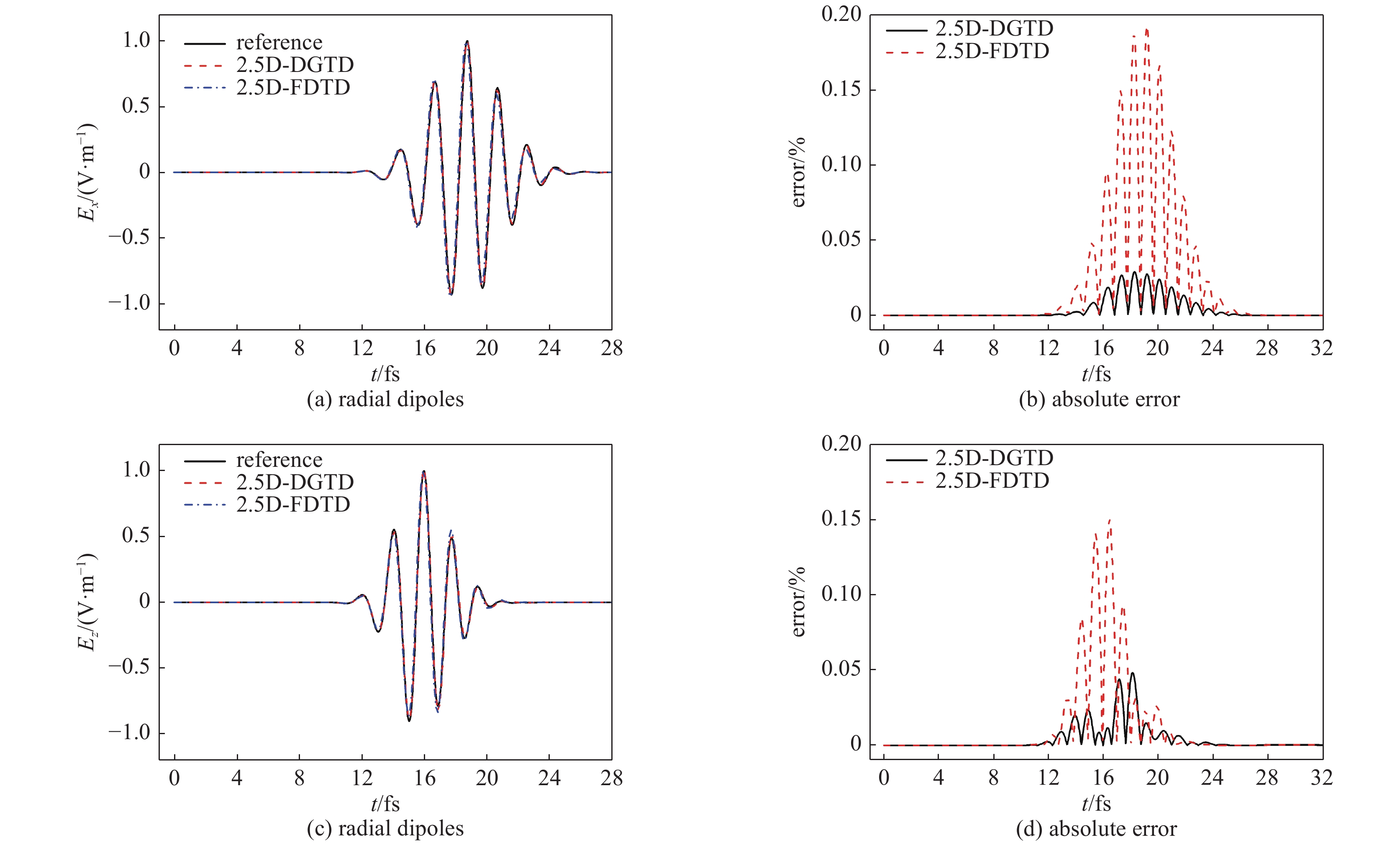
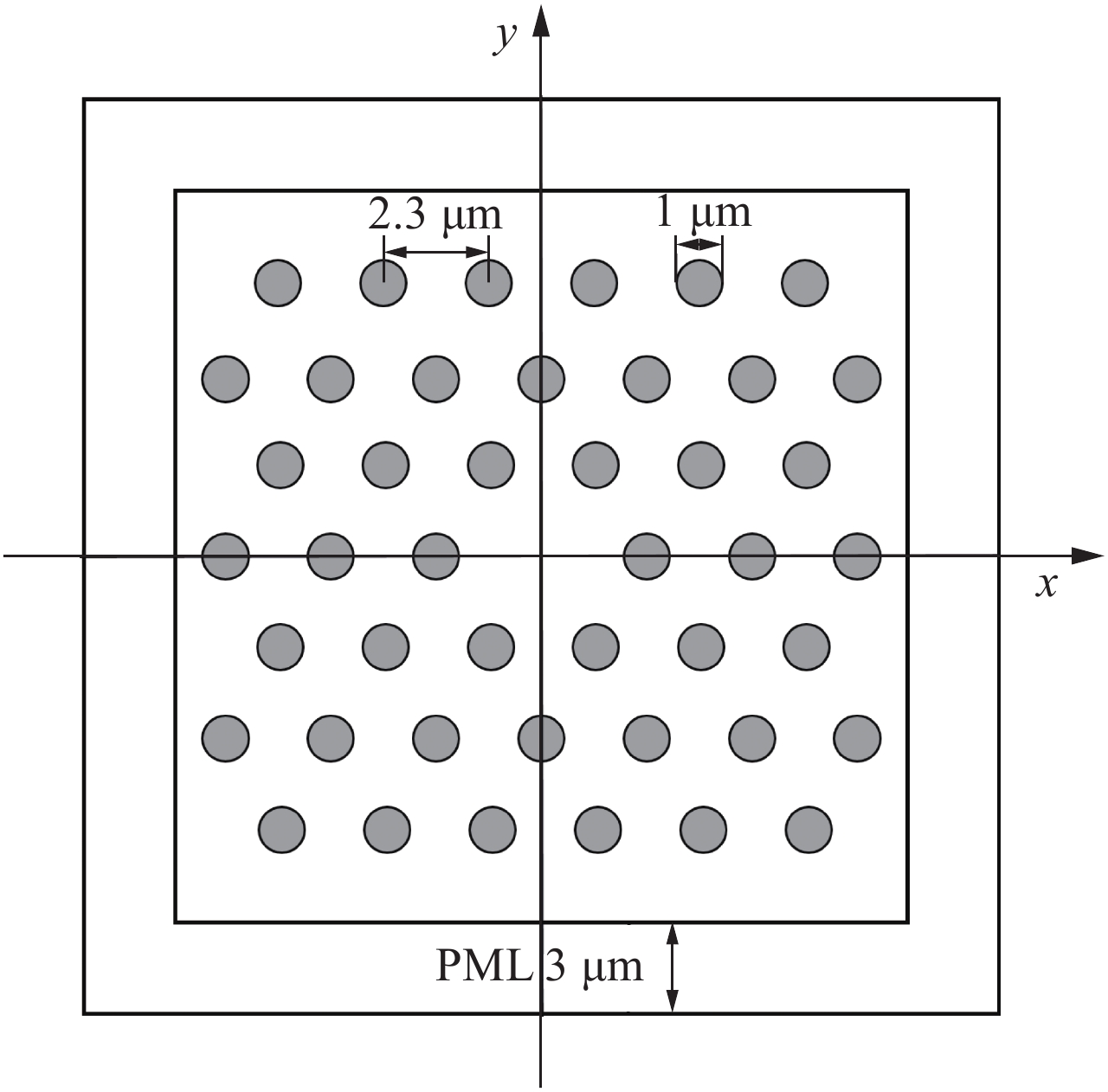
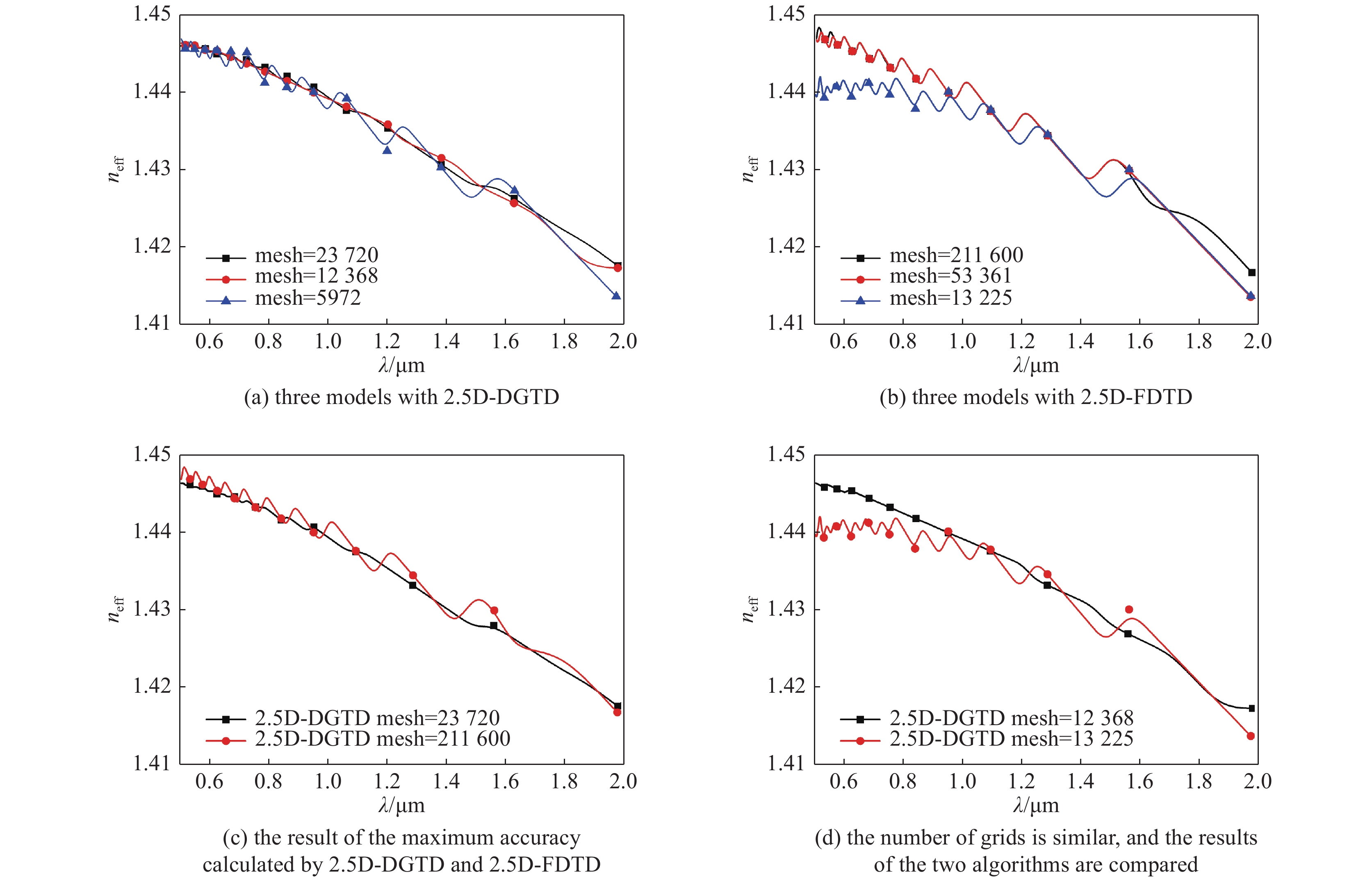
摘要: 介质沿空间固定方向均匀分布的结构在电磁导波器件中有十分广泛的应用,对这类器件的分析通常被称为2.5D电磁问题。利用器件在固定方向介质分布均匀的特点,将电磁场量沿该方向进行空间傅里叶变换,可以把对三维问题的分析转化为两维问题求解,从而极大地减小计算开销。针对传统基于差分的2.5D电磁场算法在弯曲形状逼近上有阶梯误差的缺陷,本文提出了基于三角形网格的2.5D时域间断有限元方法(DGTD),并用它模拟了电偶极子与光纤的耦合效率和光子晶体光纤的色散特性。与基于规则网格的2.5D差分方法进行对比。结果表明,文中建立的2.5D DGTD方法对弯曲形状的模拟更加逼真,计算内存占用最大减少10.4%,计算精度最大相差0.011%,计算时间缩短74.9%,计算效率提高。Abstract: In this work, a 2.5-dimensional discontinuous Galerkin time-domain(2.5D-DGTD) method with perfectly matched layer is proposed as a flexible tool to solve accurately electromagnetic problems in which media are homogeneous in one direction. Two numerical examples are simulated to demonstrate the advantages of the proposed method, which are the coupling between an electric dipole and optical fiber, and the analysis of dispersion characteristics of a photonic crystal fiber. The method is compare with the traditional 2.5-dimensional finite-difference time-domain method. The results show that the 2.5D-DGTD method is more realistic, especially for the simulation of curved shapes, where compared the calculation memory is reduced by 10.4%, the calculation accuracy differs by 0.011%, the calculation time is shortened, and the calculation efficiency is increased by 74.9%.
-
表 1 两种算法消耗计算资源的比较
Table 1. Comparison of two algorithms consuming computing resources
method mesh ${\Delta _t}/fs$ memory/MB time/s 2.5D-FDTD 625 0.094 261.5 823 2.5D-DGTD 432 0.013 227.4 217 表 2 不同算法的有效折射率
Table 2. Fundamental effective index of different algorithms
method mesh result relative error/% 2.5D-FDTD 211 600 1.428 72 0.002 8 52 900 1.428 78 0.007 0 13 225 1.428 84 0.011 2 2.5D-DGTD 23 720 1.428 69 0.000 7 12 368 1.428 71 0.002 1 5 972 1.428 71 0.002 1 3D-full-vector finite difference[20] 14 400 1.428 68 − 表 3 两种算法消耗计算资源的比较
Table 3. Comparison of two algorithms consuming computing resources
method $\Delta l/{\rm{um}}$ mesh ${\Delta _{ {\rm{t} },\max} }/{\rm{fs}}$ memory/GB time/s 2.5D-FDTD 0.047 92 211 600 0.112 1.4 22 812 0.095 65 52 900 0.225 0.34 3 083 0.191 67 132 25 0.451 0.07 432 2.5D-DGTD 0.106 67 23 720 0.280 0.874 5 732 0.144 14 12 368 0.285 0.458 3 225 0.207 79 5 972 0.360 0.229 1 394 -
[1] Ibanescu M, Fink Y, Fan S, et al. An all-dielectric coaxial waveguide[J]. Science, 2000, 289(5478): 415-419. doi: 10.1126/science.289.5478.415 [2] Russell P. Photonic crystal fibers[J]. Science, 2003, 299(5605): 358-362. doi: 10.1126/science.1079280 [3] Moghaddam M, Chew W C, Anderson B, et al. Computation of transient electromagnetic waves in inhomogeneous media[J]. Radio Science, 2016, 26(1): 265-273. [4] Moghaddam M, Chew W C, Anderson B, et al. Computation of transient electromagnetic waves in inhomogeneous media[J]. Radio Science, 1991, 26(1): 265-273. doi: 10.1029/90RS00924 [5] Yee K S. Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media[J]. IEEE Transactions on Antennas & Propagation, 1966, 14(5): 302-307. [6] Tang Zibin, Liu Qing Huo. The 2.5D FDTD and Fourier PSTD methods and applications[J]. Microwave & Optical Technology Letters, 2003, 36(6): 430-436. [7] Belli K, Rappaport C M, Zhan H, et al. Effectiveness of 2-D and 2.5-D FDTD ground-penetrating radar modeling for bridge-deck deterioration evaluated by 3-D FDTD[J]. IEEE Transactions on Geoscience & Remote Sensing, 2009, 47(11): 3656-3663. [8] Namiki T. A new FDTD algorithm based on alternating-direction implicit method[J]. IEEE Transactions on Microwave Theory and Techniques, 1999, 47(10): 2003-2007. doi: 10.1109/22.795075 [9] 刘宗信, 陈亦望, 徐鑫, 等. 三维周期结构弱无条件稳定时域有限差分算法[J]. 强激光与粒子束, 2012, 24(11):2687-2692. (Liu Zongxin, Chen Yiwang, Xu Xin, et al. Weakly conditionally stable 3-D FDTD method for periodic structures[J]. High Power Laser and Particle Beams, 2012, 24(11): 2687-2692 doi: 10.3788/HPLPB20122411.2687 [10] Volakis J L, Chatterjee A, Kempel L C. Finite element method electromagnetics : Antennas, microwave circuits, and scattering applications[M]. Piscataway: IEEE Press, 1998. [11] Kong F N, Johnstad S E, Røsten T, et al. A 2.5D finite-element-modeling difference method for marine CSEM modeling in stratified anisotropic media[J]. Geophysics, 2008, 73(1): 9-19. [12] Ou Yangxin, David P, Chen Y. Fourier finite element modeling of light emission in waveguides: 2.5-dimensional FEM approach[J]. Optics express, 2015, 23(23): 30259-30269. doi: 10.1364/OE.23.030259 [13] Ainsworth M. Dispersive and dissipative behaviour of high order discontinuous Galerkin finite element methods[J]. Journal of Computational Physics, 2008, 198(1): 106-130. [14] Hu F Q, Hussaini M Y, Rasetarinera P. An analysis of the discontinuous Galerkin method for wave propagation problems[J]. Journal of Computational Physics, 1999, 151(2): 921-946. doi: 10.1006/jcph.1999.6227 [15] Hesthaven J S, Warburton T. High-order nodal discontinuous Galerkin methods for the Maxwell eigenvalue problem[J]. Philosophical Transactions, 2004, 362(1816): 493-524. doi: 10.1098/rsta.2003.1332 [16] Kennedy C A, Carpenter M H, Lewis R M. Low-storage, explicit Runge–Kutta schemes for the compressible Navier–Stokes equations[J]. Applied Numerical Mathematics, 2000, 35(3): 177-219. doi: 10.1016/S0168-9274(99)00141-5 [17] Chen Geng, Zhao Lei, Yu Wenhua, et al. A general scheme for the discontinuous Galerkin time-domain modeling and S-parameter extraction of inhomogeneous waveports[J]. IEEE Transactions on Microwave Theory and Techniques, 2018, 66(4): 1701-1712. doi: 10.1109/TMTT.2017.2785800 [18] Almokhtar M, Fujiwara M, Takashima H, et al. Numerical simulations of nanodiamond nitrogen-vacancy centers coupled with tapered optical fibers as hybrid quantum nanophotonic devices[J]. Optics Express, 2014, 22(17): 20045-20059. doi: 10.1364/OE.22.020045 [19] 栗岩锋, 刘博文, 王子涵, 等. 光子晶体光纤色散的有限差分法研究[J]. 中国激光, 2004, 31(10):1257-1260. (Li Yanfeng, Liu Bowen, Wang Zihan, et al. Finite difference analysis of dispersion properties of photonic crystal fibers[J]. Chinese Journal of Lasers, 2004, 31(10): 1257-1260 doi: 10.3321/j.issn:0258-7025.2004.10.023 [20] Zhu Zhaoming, Thomas G B. Full-vectorial finite-difference analysis of microstructured optical fibers[J]. Optics express, 2002, 10(17): 853-864. doi: 10.1364/OE.10.000853 -




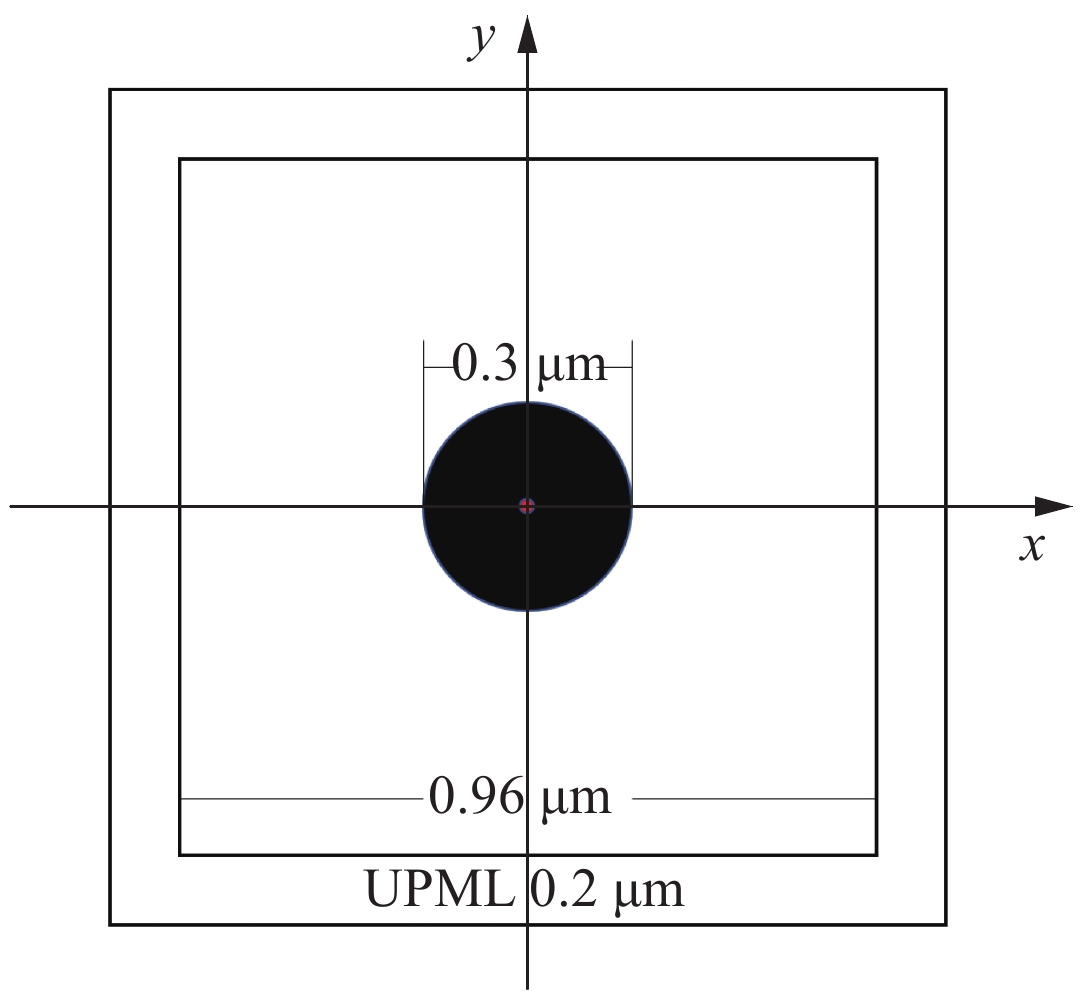
 下载:
下载: