Measurement of transverse phase space based on machine learning
-
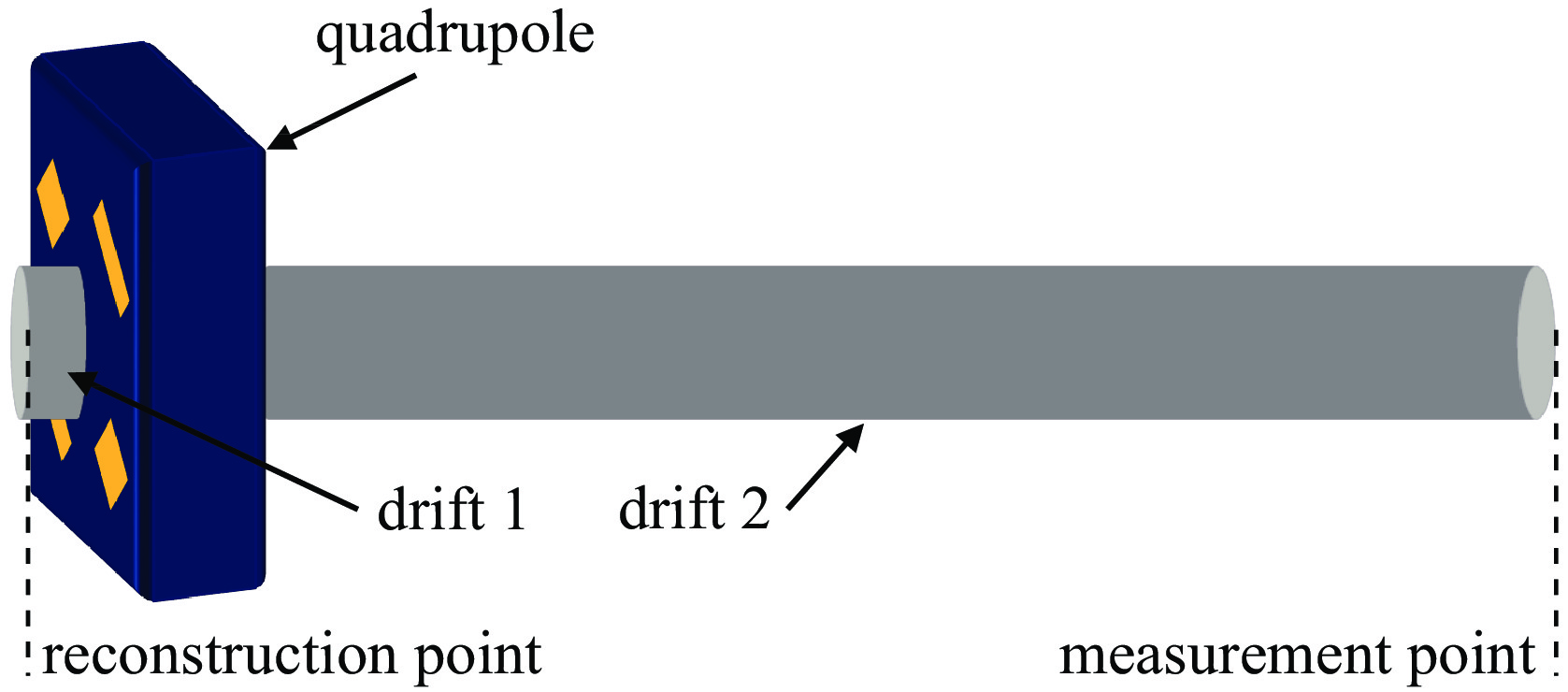
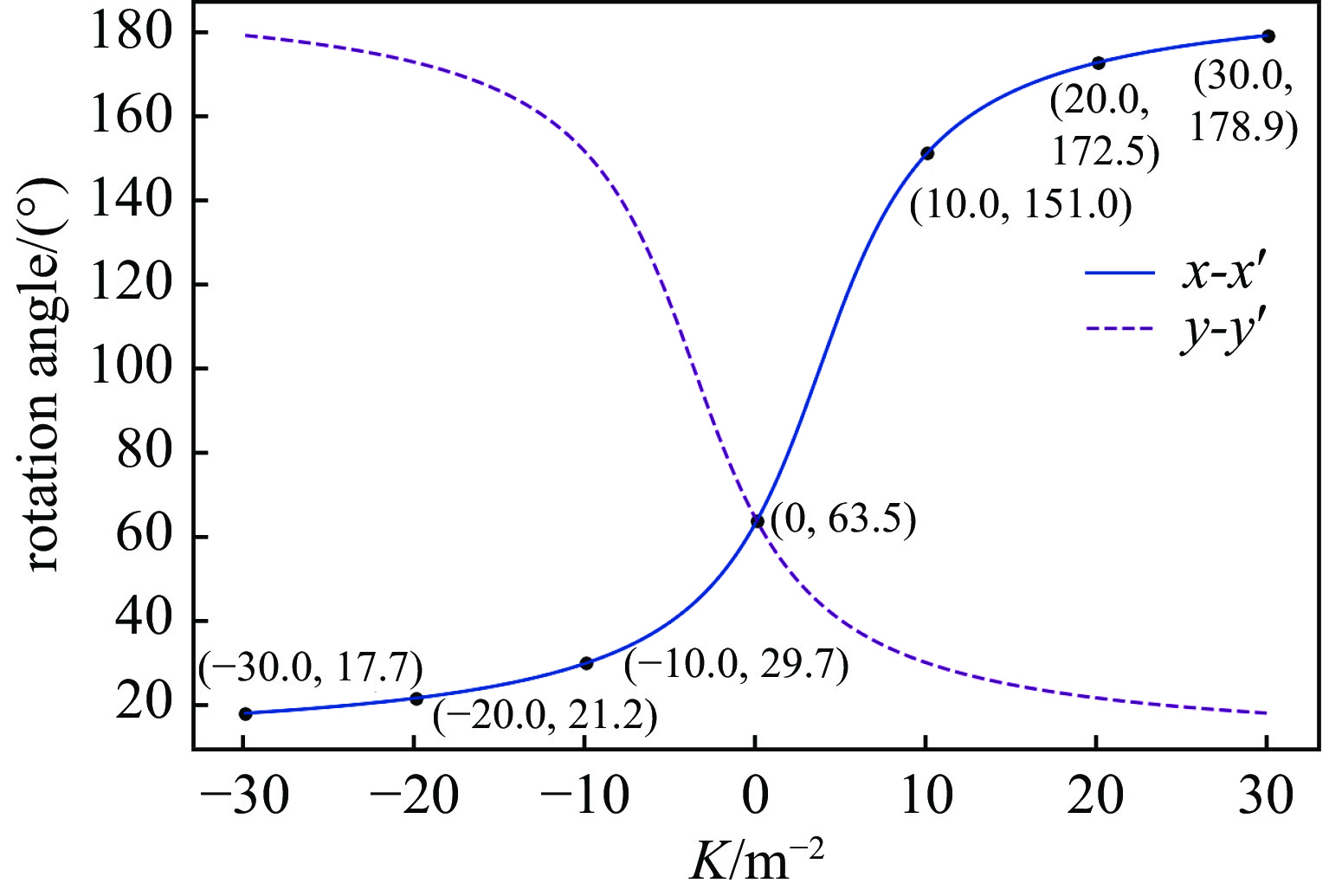
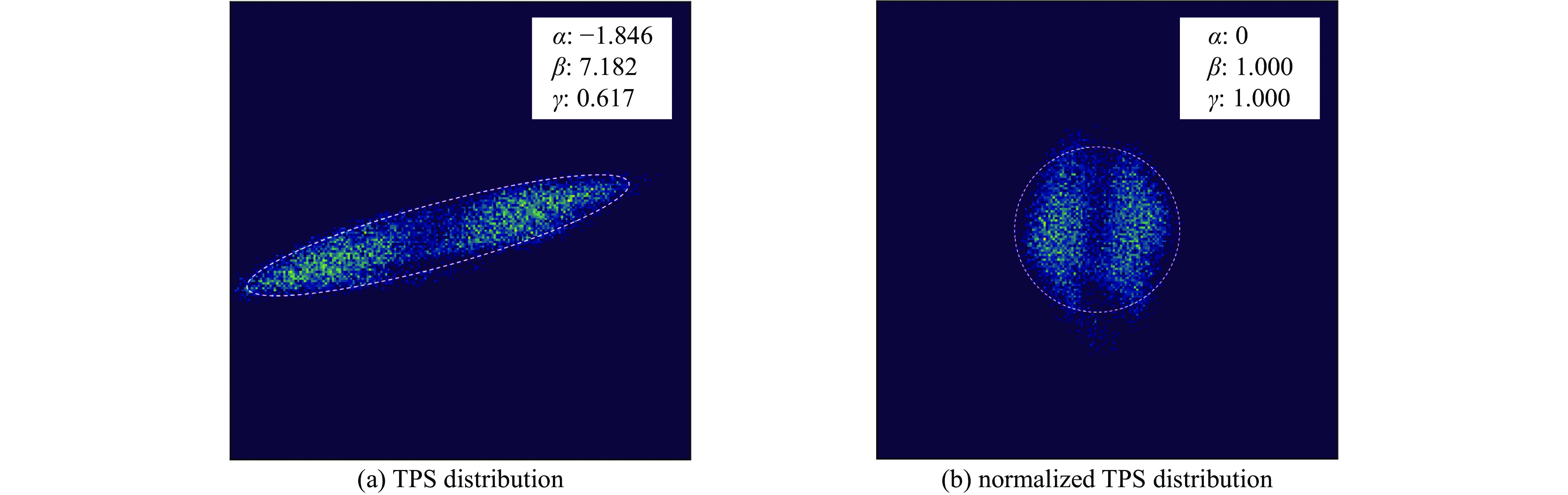
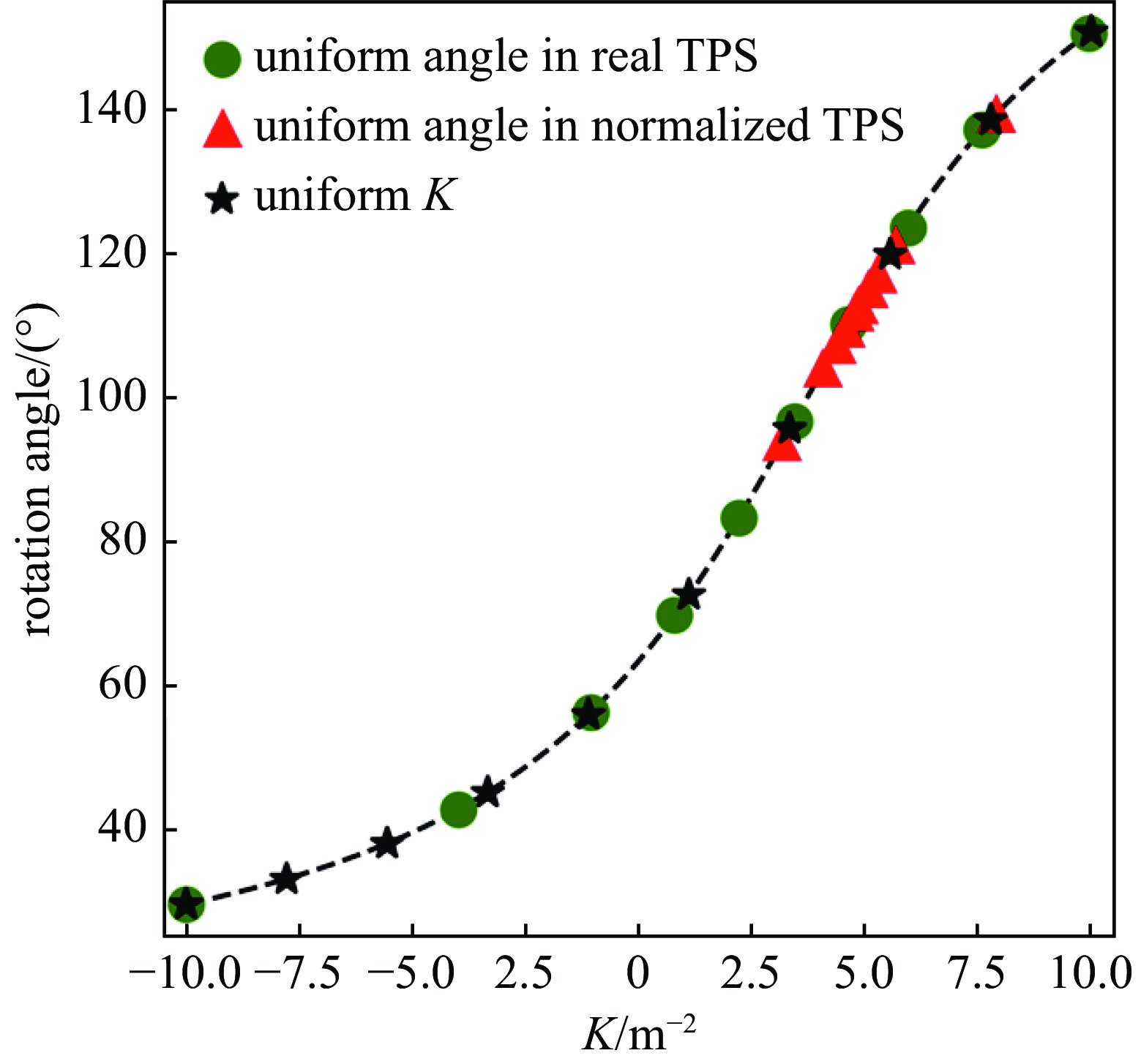
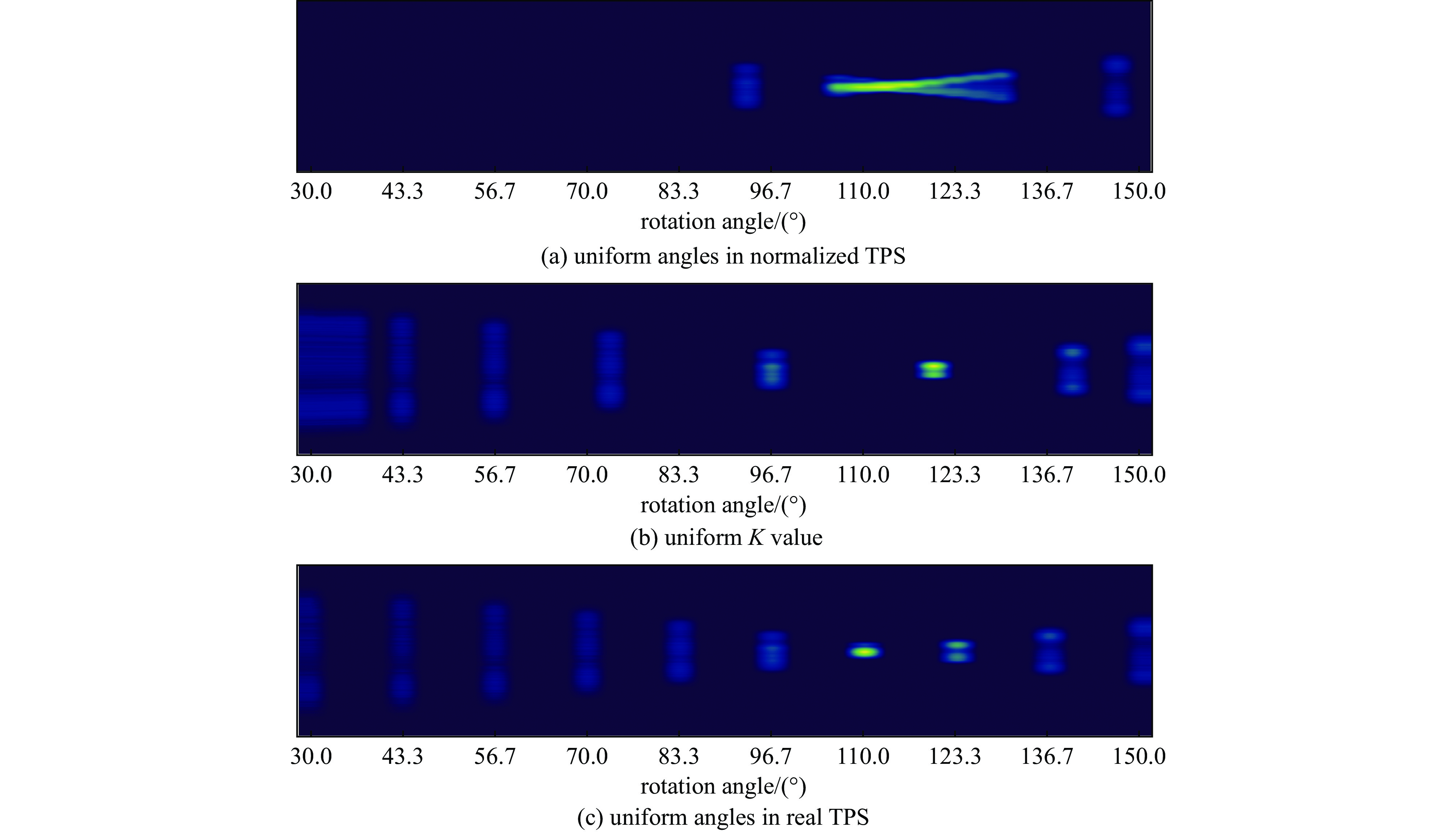
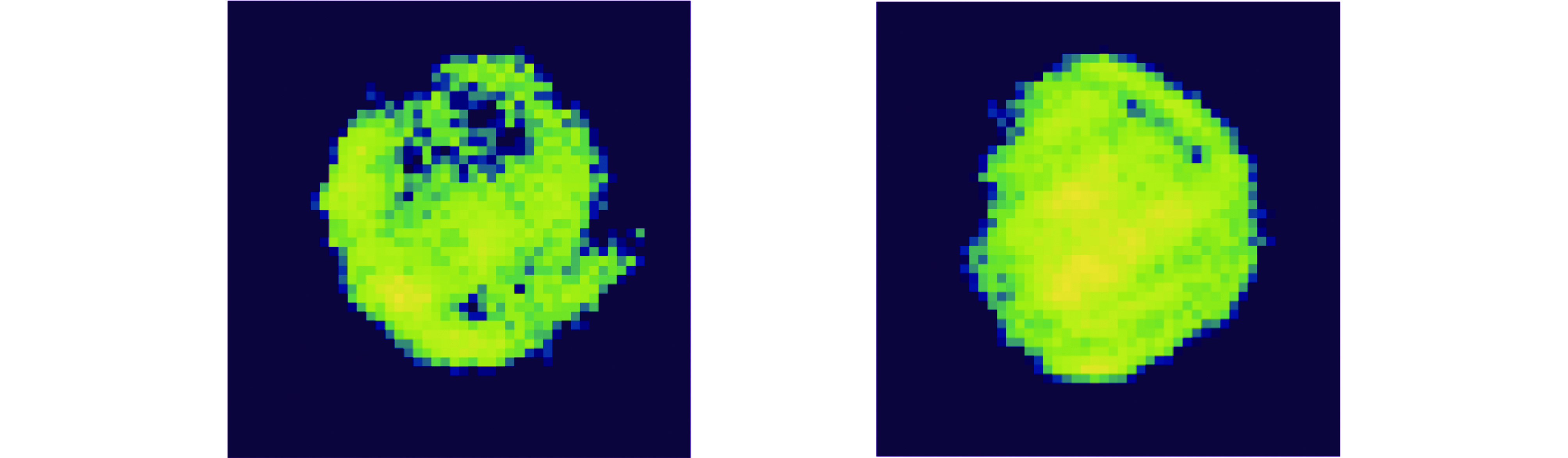
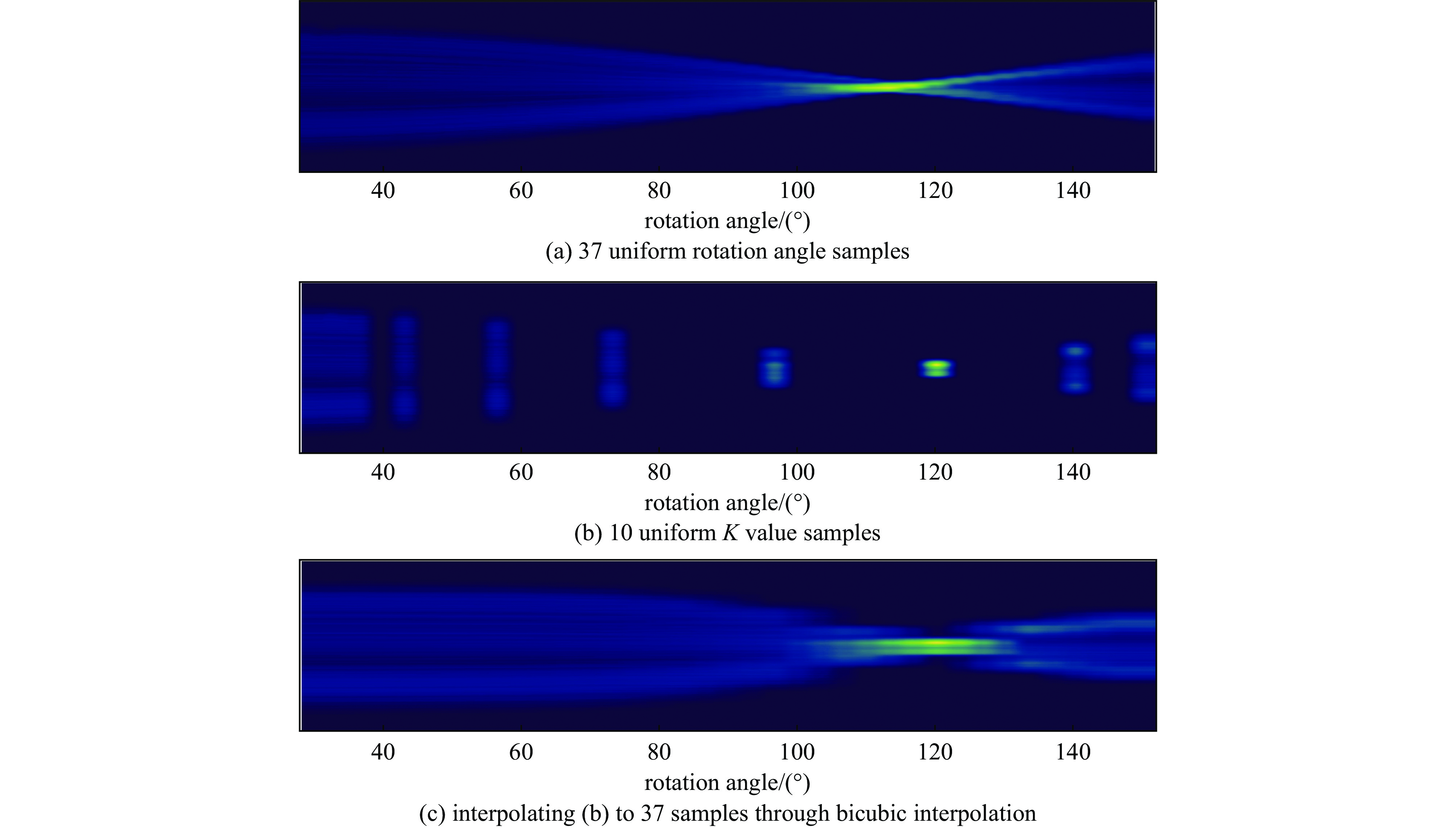
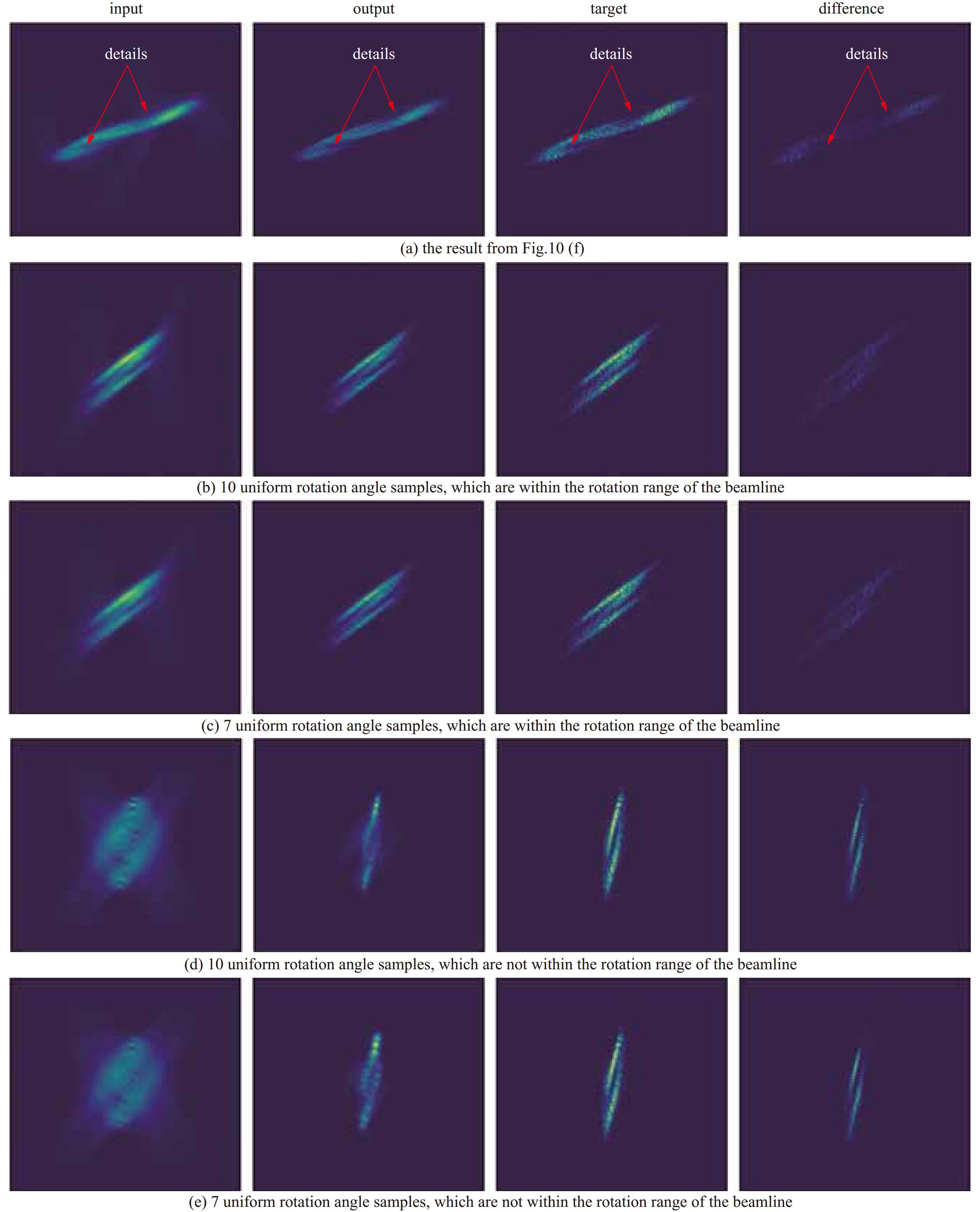
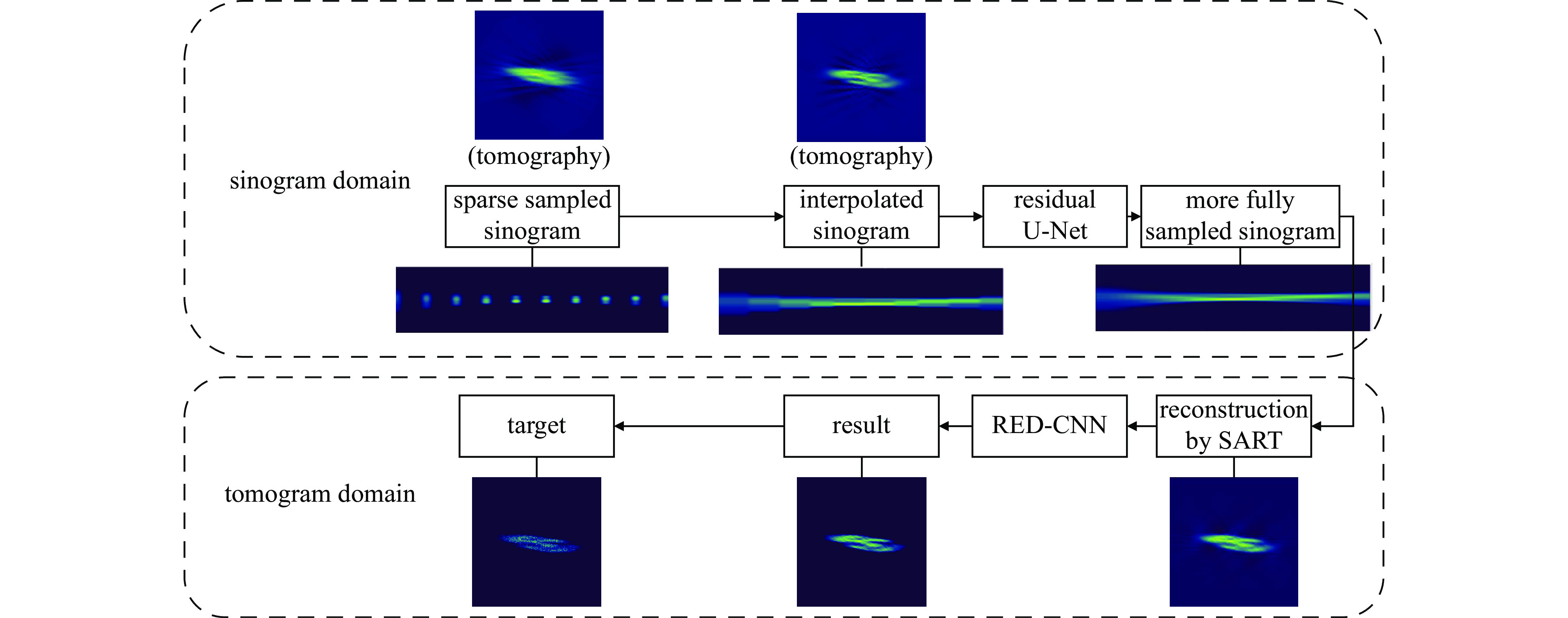
摘要: 理论上,使用断层扫描技术可以得到真实的横向相空间分布。但是想要更加精确地了解分布的细节,需要解决旋转角度范围受限和投影数目不足的问题。针对这两个问题,提出了在混合域处理的神经网络模型,即组合地在正弦域和断层域分别使用插值和去除伪影神经网络。在简单地测量束线以及投影数目比较少(7个)的情况下,该网络模型也能高质量地重建束团横向相空间分布。并且,由于选择旋转角度的方式和归一化相空间无关,因此,无需测量Twiss参数。采用该方法测量束团横向相空间,一定程度提升了重建质量,简化了测量的方式。Abstract: Accurate measurement of the transverse phase space distribution of electron beams is of great importance in the design and optimization of accelerators. The computerized tomography theoretically provides the true transverse phase space distribution. However, to understand the details of the distribution more accurately, it is necessary to solve the problems of limited range of rotation angle and insufficient number of projections. In this paper, a neural network model is proposed to address these two problems in the hybrid domains, which combines interpolation and artifact removal neural networks in the sinogram and tomogram domains, respectively. Even with a simple diagnostic beamline and a small number of projections (7), the network model can reconstruct the transverse phase space distribution of beams with high quality. Moreover, since the selection of angles is independent of the normalized phase space, Twiss parameters do not need to be measured. Using the proposed method to measure the transverse phase space improves reconstruction quality to a certain extent and simplifies the measurement process.
-
Key words:
- transverse phase space /
- computerized tomography /
- machine learning /
- neural network
-
表 1 Residual U-Net 网络参数
Table 1. Residual U-Net network parameter settings
name parameters output Conv_block_1 1 $ \times $1 conv, 64 200 $ \times $57, 64 3 $ \times $3 conv, 64 Conv_block_2 2 $ \times $3 conv, s=2, p=0, 64 100 $ \times $28, 64 [3 $ \times $3 conv, 64] $ \times $2 Conv_block_3 2 $ \times $2 conv, s=2, p=0, 64 50 $ \times $14, 64 [3 $ \times $3 conv, 64] $ \times $2 Conv_block_4 2 $ \times $2 conv, s=2, p=0, 64 25 $ \times $7, 64 [3 $ \times $3 conv, 64] $ \times $2 ConvT_block_1 $2 \times 2$ convT, s=2, p=0, 64 50 $ \times $14, 64 ConvT_block_2 Conv_block_3, concatenation 100 $ \times $28, 64 [ $3 \times 3$ conv,64] $ \times $2 $2 \times 2$ convT, s=2, p=0, 64 ConvT_block_3 Conv_block_2, concatenation 200 $ \times $57, 64 [ $3 \times 3$ conv, 64] $ \times $2 $2 \times 3$ convT, s=2, p=0, 64 Conv_block_5 Conv_block_1, concatenation 200 $ \times $57, 1 $3 \times 3$ conv,16 $3 \times 3$ conv, 1 shortcut connection 表 2 RED-CNN 网络参数
Table 2. RED-CNN network parameter settings
name parameters output Conv_1 [5, Conv, 16] $ \times $2 192 $ \times $192, 16 Conv_2 [5, Conv, 16] $ \times $2 184 $ \times $184, 16 Conv_3 [5, Conv, 16] $ \times $2 176 $ \times $176, 16 ConvT_1 [5, ConvT, 16] $ \times $2 184 $ \times $184, 16 ConvT_2 Conv_2, addition 192 $ \times $192, 16 [5, convT, 16] $ \times $2 ConvT_3 Conv_1, addition 200 $ \times $200, 1 [5, convT1, 1] $ \times $2 shortcut connection -
[1] 赵振堂. 先进X射线光源加速器原理与关键技术[M]. 上海: 上海交通大学出版社, 2020: 164-165Zhao Zhentang. Principles and key technologies of advanced X-ray light source accelerators[M]. Shanghai: Shanghai Jiao Tong University Press, 2020: 164-165 [2] Gordon M, Li W H, Andorf M B, et al. Four-dimensional emittance measurements of ultrafast electron diffraction optics corrected up to sextupole order[J]. Physical Review Accelerators and Beams, 2022, 25: 084001. doi: 10.1103/PhysRevAccelBeams.25.084001 [3] Feist A, Bach N, Rubiano da Silva N, et al. Ultrafast transmission electron microscopy using a laser-driven field emitter: femtosecond resolution with a high coherence electron beam[J]. Ultramicroscopy, 2017, 176: 63-73. doi: 10.1016/j.ultramic.2016.12.005 [4] 杜应超, 黄文会, 唐传祥, 等. 汤姆逊散射X射线源初步实验中电子束参数测量及其对X射线性能影响的研究[J]. 高能物理与核物理, 2006, 30(s1):84-86 doi: 10.3321/j.issn:0254-3052.2006.z1.027Du Yingchao, Huang Wenhui, Tang Chuanxiang, et al. Preliminary experiments of Thomson scattering X-ray source: measurements of electron beam’s parameters and their influence on the X-ray performance[J]. High Energy Physics and Nuclear Physics, 2006, 30(s1): 84-86 doi: 10.3321/j.issn:0254-3052.2006.z1.027 [5] Brown W J, Anderson S G, Barty C P J, et al. Experimental characterization of an ultrafast Thomson scattering X-ray source with three-dimensional time and frequency-domain analysis[J]. Physical Review Accelerators and Beams, 2004, 7: 060702. doi: 10.1103/PhysRevSTAB.7.060702 [6] Nagaitsev S, Huang Z, Power J, et al. Accelerator and beam physics research goals and opportunities[R]. FERMILAB-FN-1123, 2021. [7] Behrens C, Decker F J, Ding Y, et al. Few-femtosecond time-resolved measurements of X-ray free-electron lasers[J]. Nature Communications, 2014, 5: 3762. doi: 10.1038/ncomms4762 [8] Rao Y N, Baartman R. Transverse phase space tomography in TRIUMf injection beamline[C]//Proceedings of IPAC2011. 2011. [9] Yu Qinglin, Gu Duan, Zhang Meng, et al. Transverse phase space reconstruction study in Shanghai soft X-ray FEL facility[J]. Nuclear Science and Techniques, 2018, 29: 9. doi: 10.1007/s41365-017-0338-0 [10] McKee C B, O’Shea P G, Madey J M J. Phase space tomography of relativistic electron beams[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 1995, 358(1/3): 264-267. [11] Hermann B, Guzenko V A, Hürzeler O R, et al. Electron beam transverse phase space tomography using nanofabricated wire scanners with submicrometer resolution[J]. Physical Review Accelerators and Beams, 2021, 24: 022802. doi: 10.1103/PhysRevAccelBeams.24.022802 [12] 杜应超, 向导, 黄文会, 等. 基于CT算法的束团横向相空间测量[J]. 高能物理与核物理, 2006, 30(9):888-891 doi: 10.3321/j.issn:0254-3052.2006.09.015Du Yingchao, Xiang Dao, Huang Wenhui, et al. Transverse phase space measurement based on computerized tomography[J]. High Energy Physics and Nuclear Physics, 2006, 30(9): 888-891 doi: 10.3321/j.issn:0254-3052.2006.09.015 [13] Tuy H K. An inversion formula for cone-beam reconstruction[J]. SIAM Journal on Applied Mathematics, 1983, 43(3): 546-552. doi: 10.1137/0143035 [14] Romanov A. Beam phase space tomography at fast electron linac at Fermilab[R]. FERMILAB-CONF-18-321-AD, 2018. [15] Stratakis D, Kishek R A, Li H, et al. Tomography as a diagnostic tool for phase space mapping of intense particle beams[J]. Physical Review Accelerators and Beams, 2006, 9: 112801. doi: 10.1103/PhysRevSTAB.9.112801 [16] Andersen A H, Kak A C. Simultaneous algebraic reconstruction technique (SART): a superior implementation of the ART algorithm[J]. Ultrasonic Imaging, 1984, 6(1): 81-94. doi: 10.1177/016173468400600107 [17] Hock K M, Ibison M G. A study of the maximum entropy technique for phase space tomography[J]. Journal of Instrumentation, 2013, 8: P02003. doi: 10.1088/1748-0221/8/02/P02003 [18] Scheinker A, Cropp F, Paiagua S, et al. Adaptive deep learning for time-varying systems with hidden parameters: predicting changing input beam distributions of compact particle accelerators[J]. 2021.doi: 10.21203/rs.3.rs-373311/v1. [19] Wang Minwen, Wang Zhongming, Wang Di, et al. Four-dimensional phase space measurement using multiple two-dimensional profiles[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2019, 943: 162438. [20] Hock K M, Ibison M G, Holder D J, et al. Beam tomography in transverse normalised phase space[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2011, 642(1): 36-44. [21] 于清林. 束团横向相空间重建技术研究[D]. 上海: 中国科学院大学(中国科学院上海应用物理研究所), 2018Yu Qinglin. Study on beam transverse phase space reconstruction technology[D]. Shanghai: Chinese Academy of Sciences (Shanghai Institute of Applied Physics), 2018 [22] Wang Ge, Ye J C, De Man B. Deep learning for tomographic image reconstruction[J]. Nature Machine Intelligence, 2020, 2(12): 737-748. doi: 10.1038/s42256-020-00273-z [23] Wolski A, Johnson M A, King M, et al. Transverse phase space tomography in an accelerator test facility using image compression and machine learning[J]. Physical Review Accelerators and Beams, 2022, 25: 122803. doi: 10.1103/PhysRevAccelBeams.25.122803 [24] Radon J. Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten[J]. Berichte uber die Verhandlungen Gesellshaft der Wissenschaften zu Leipzig. Journal of Mathematical Physics, 1917, 69: 262-277. [25] Hounsfield G N. Computerized transverse axial scanning (tomography): Part 1. Description of system[J]. The British Journal of Radiology, 1973, 46(552): 1016-1022. doi: 10.1259/0007-1285-46-552-1016 [26] Sander O R, Minerbo G N, Jameson R A, et al. Beam tomography in two and four dimensions [100 MeV H+/ beams and 750 keV H− beams][R]. LA-UR-79-2540; CONF-790927-20, 1979: 6. [27] Lee D, Choi S, Kim H J. High quality imaging from sparsely sampled computed tomography data with deep learning and wavelet transform in various domains[J]. Medical Physics, 2019, 46(1): 104-115. doi: 10.1002/mp.13258 [28] 刘勇. 插值技术及其在CT重建中的应用[D]. 天津: 天津职业技术师范大学, 2022Liu Yong. Interpolation technology and its application in CT reconstruction[D]. Tianjin: Tianjin University of Technology and Education, 2022 [29] Kalke M, Siltanen S. Sinogram interpolation method for sparse-angle tomography[J]. Applied Mathematics, 2014, 5(3): 423-441. doi: 10.4236/am.2014.53043 [30] Han Y S, Yoo J, Ye J C. Deep residual learning for compressed sensing CT reconstruction via persistent homology analysis[DB/OL]. arXiv preprint arXiv: 1611.06391, 2016. [31] Ronneberger O, Fischer P, Brox T. U-Net: convolutional networks for biomedical image segmentation[C]//Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention. 2015. [32] Yu Yang, Gong Zhiqiang, Zhong Ping, et al. Unsupervised representation learning with deep convolutional neural network for remote sensing images[C]//Proceedings of the 9th International Conference on Image and Graphics. 2017. [33] Chen Hu, Zhang Yi, Kalra M K, et al. Low-dose CT with a residual encoder-decoder convolutional neural network[J]. IEEE Transactions on Medical Imaging, 2017, 36(12): 2524-2535. doi: 10.1109/TMI.2017.2715284 [34] Xiang Dao, Du Yingchao, Yan Lixin, et al. Transverse phase space tomography using a solenoid applied to a thermal emittance measurement[J]. Physical Review Accelerators and Beams, 2009, 12: 022801. doi: 10.1103/PhysRevSTAB.12.022801 [35] Roussel R, Edelen A, Mayes C, et al. Phase space reconstruction from accelerator beam measurements using neural networks and differentiable simulations[DB/OL]. arXiv preprint arXiv: 2209.04505, 2023. [36] ASTRA. Klaus floettmann DESY[CP/OL]. Hamburg, Germany: DESY, 2017. https://www.desy.de/~mpyflo/. [37] Gupta L. Measured Data set[Z/OL]. V1. Harvard Dataverse, 2021. https://doi.org/10.7910/DVN/MVE1YC. [38] Hock K M, Wolski A. Tomographic reconstruction of the full 4D transverse phase space[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2013, 726: 8-16. [39] 杜应超. 基于CT算法的高亮度电子束六维相空间分布的测量研究[R]. 2011: 8Du Yingchao. Measurement of six dimensional phase space distribution of high brightness electron beam based on CT algorithm[R]. 2011: 8 -




 下载:
下载: