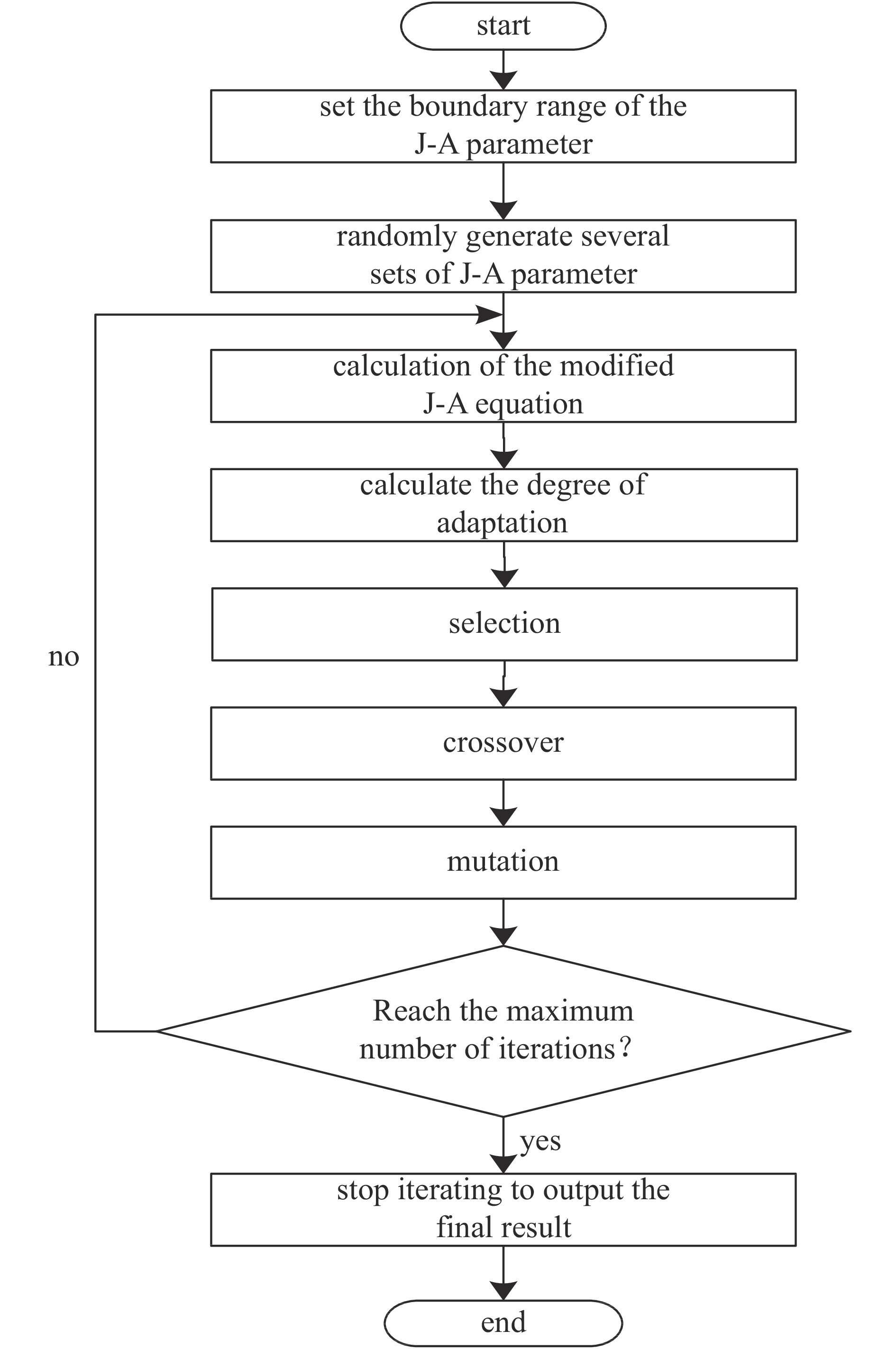
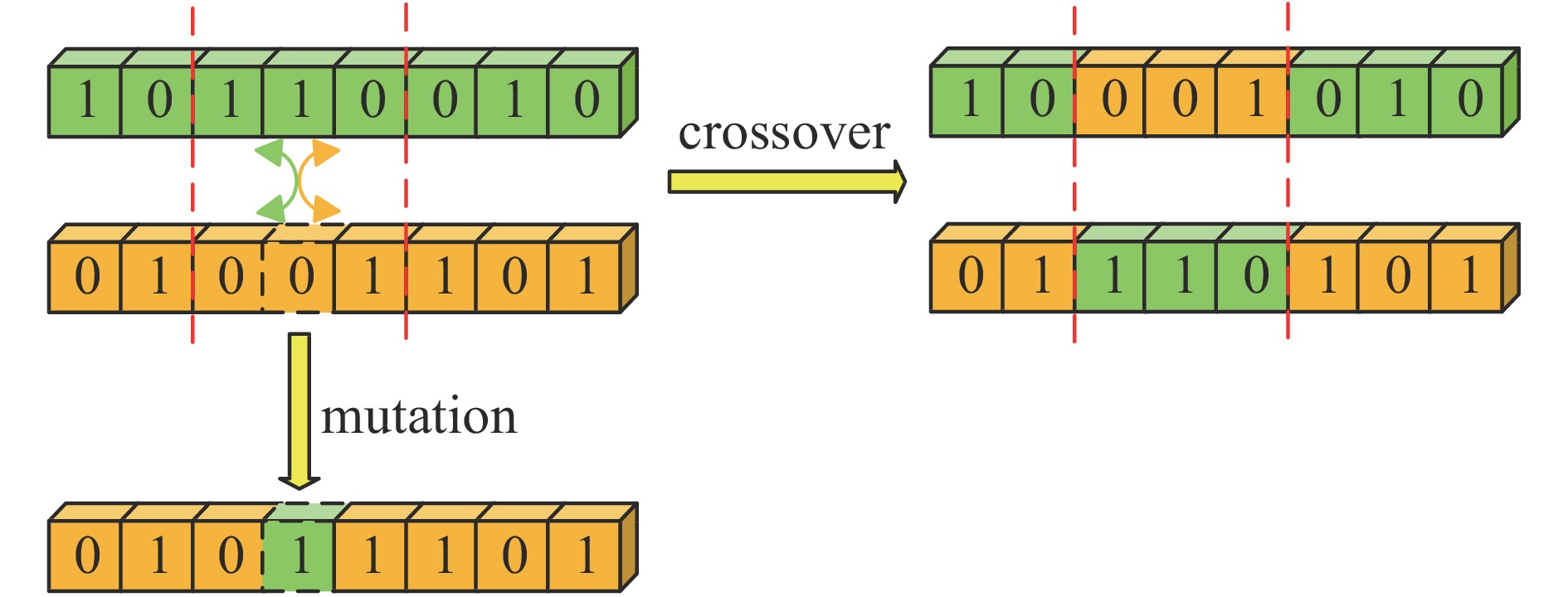
Parameter identification and application of Jiles-Atherton model for Fe-based nanocrystalline cores under pulsed excitation
-
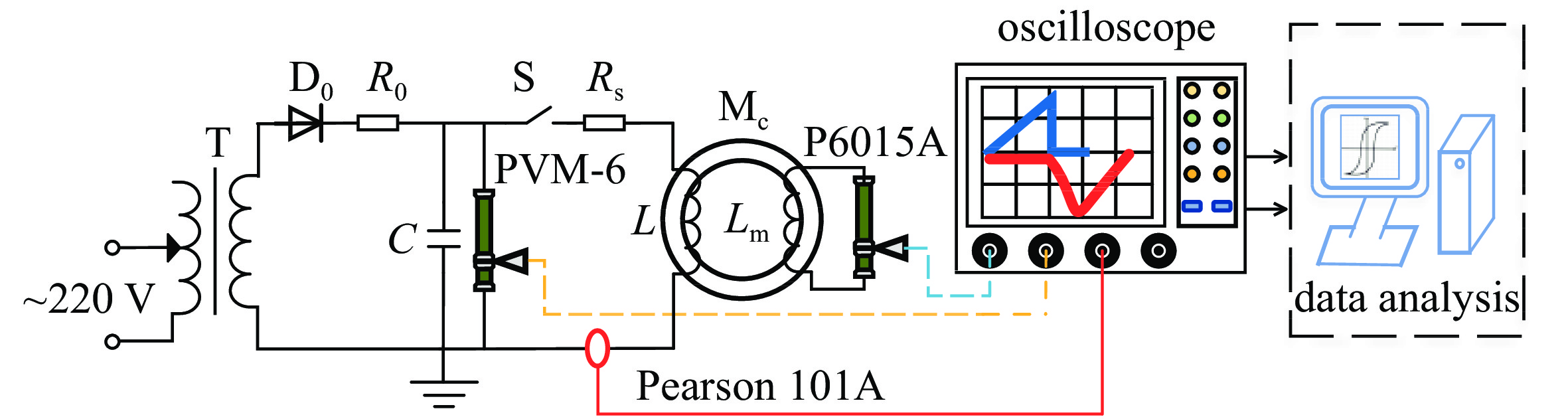
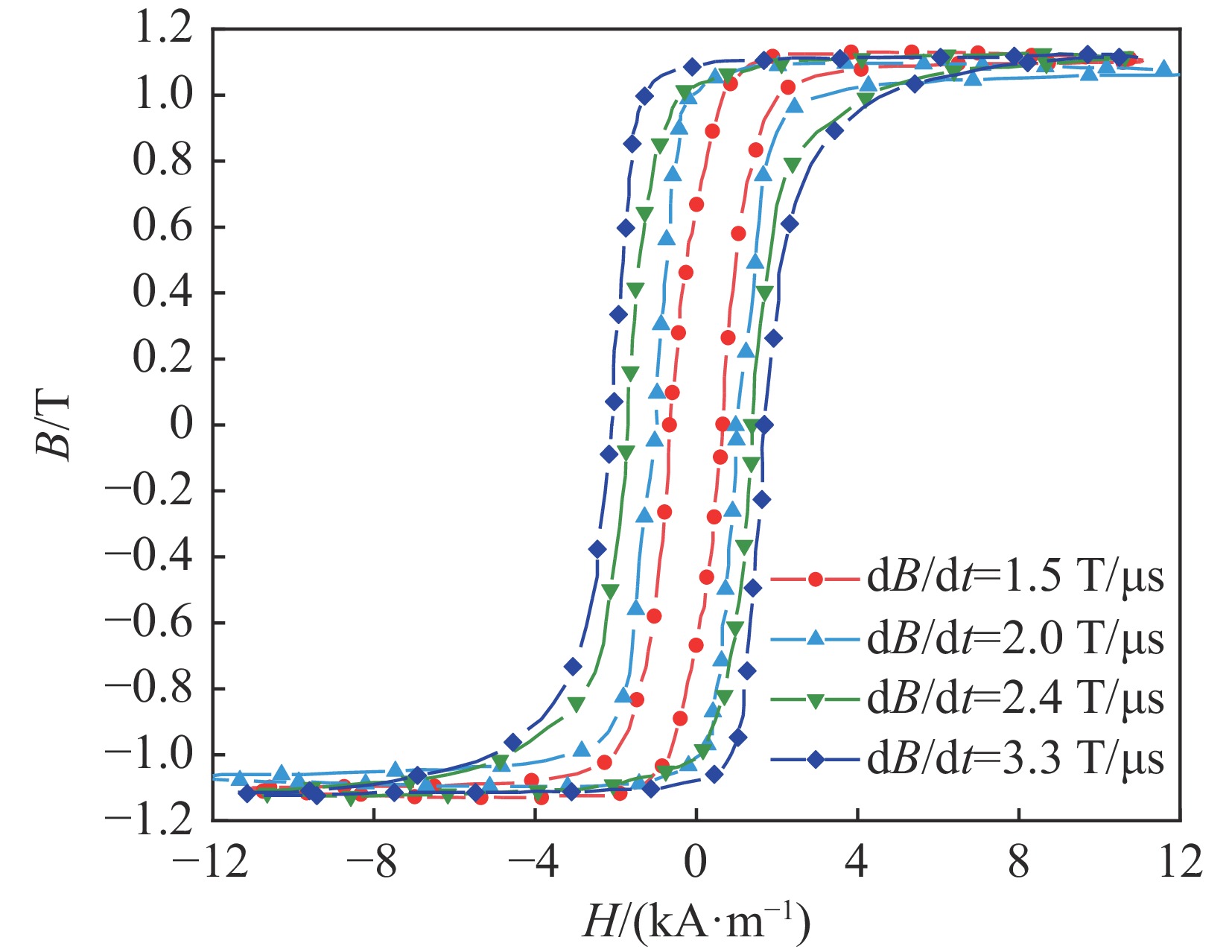
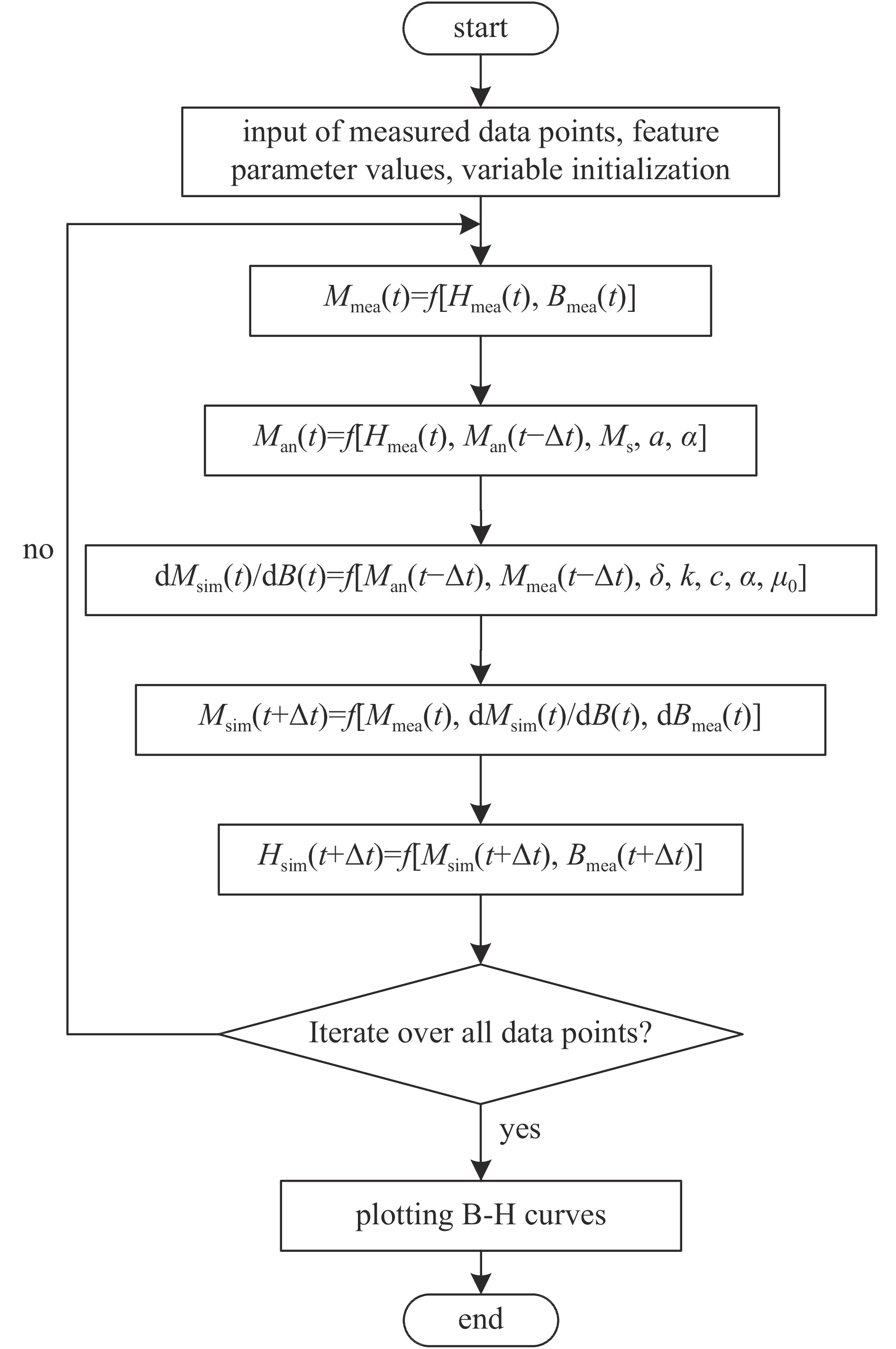
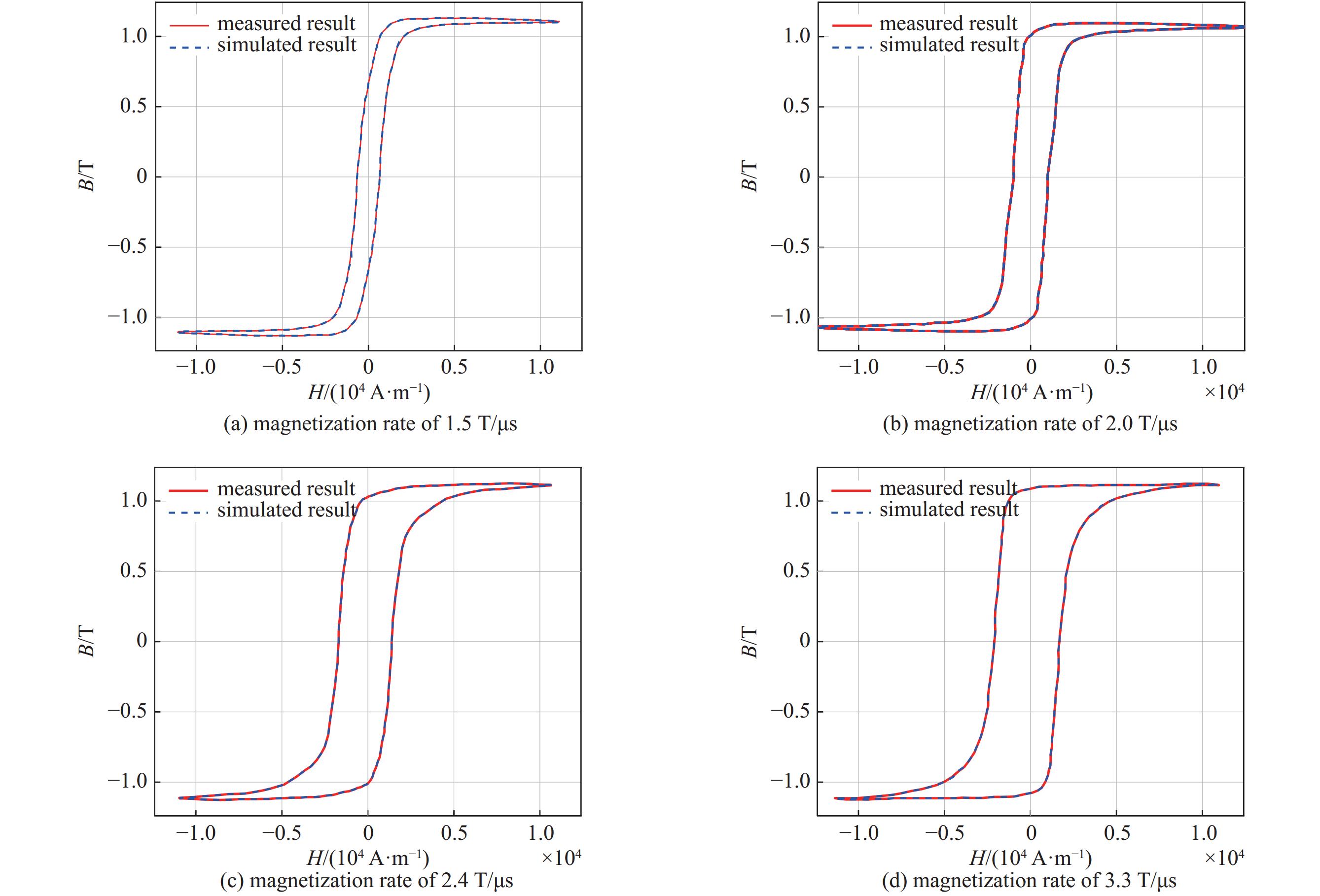
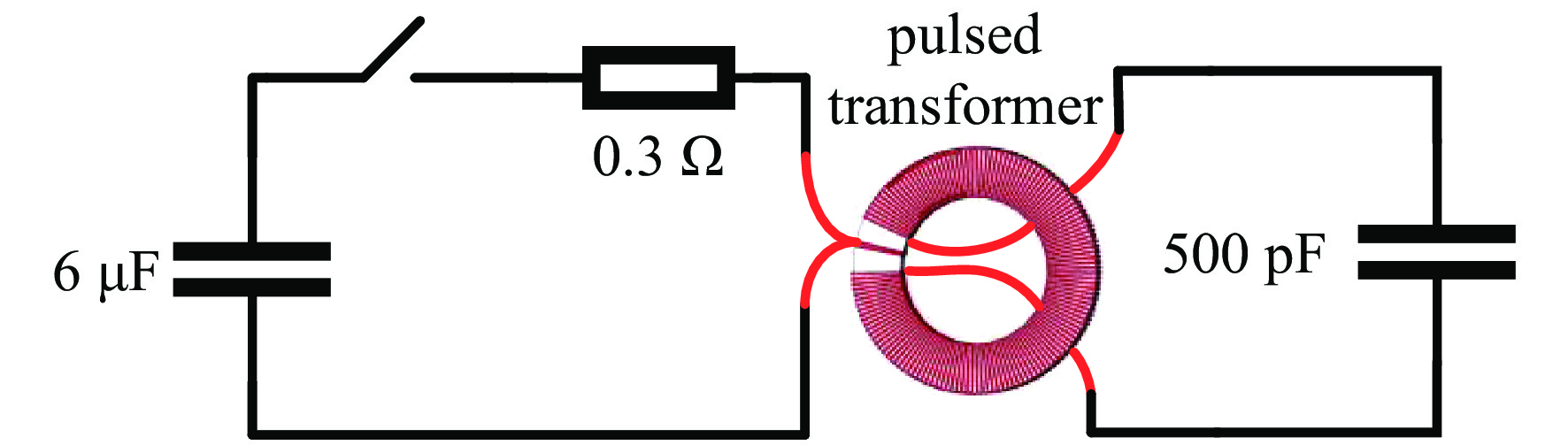
摘要: 通过理论分析对经典J-A方程进行了修正，增强了其在脉冲条件下的适应性，利用脉冲磁化特性实验平台，测量了铁基纳米晶磁芯在不同磁化速率下的磁滞回线，采用遗传算法进行脉冲激励下的J-A参数辨识，将算法模拟的磁滞回线与实验测试的磁滞回线数据集进行拟合，验证了修正后的J-A方程的有效性，最后将遗传算法寻优得到的J-A参数应用于脉冲变压器场路耦合模型的磁芯J-A参数定义中，分析脉冲变压器初级电压为1.5 kV时的仿真与实验误差，得到脉冲变压器输出波形的脉冲前沿误差为3.33%，幅值误差为2.91%，相比于J-A参数的常规非线性求解方法精度更高，能更好地应用于脉冲功率系统中含磁性元件的建模仿真。
-
关键词:
- 铁基纳米晶 /
- 脉冲磁化特性 /
- Jiles-Atherton模型 /
- 遗传算法 /
- 脉冲变压器
Abstract: The classical Jiles-Atherton (J-A) equation has been modified through theoretical analysis, which enhances its adaptability under pulsed conditions. Hysteresis loops of Fe-based nanocrystalline cores are measured at different magnetization rates by using an experimental platform for pulsed magnetization properties. The genetic algorithm (GA) is used for J-A parameter identification under pulsed excitation, and the validity of the modified J-A equations is verified by fitting the algorithmically simulated hysteresis loops to the experimentally tested hysteresis loop dataset. Finally, the J-A parameter obtained by GA optimization are applied to the definition of magnetic core parameters in the field-circuit coupling model of the pulse transformer, the simulation and experimental errors when the primary voltage of the pulse transformer is 1.5 kV are analyzed. The results show that the pulse front error of the output waveform is 3.33% and the amplitude error is 2.91%, which is more accurate than the conventional nonlinear solving method of J-A parameter. This indicates that the optimized J-A parameter can be better applied to the modeling and simulation of magnetic-containing components in pulsed power systems. -
图 2 脉冲激励下磁芯测试系统示意图
Figure 2. Schematic diagram of magnetic core test system under pulse excitation
图 8 不同磁化速率下的铁基纳米晶磁芯磁滞回线拟合图
Figure 8. Hysteresis loops fit of Fe-based nanocrystal cores at different magnetization rates
表 1 初始编码表
Table 1. Initial coding table
$ M_{\mathrm{s}}/(\mathrm{A\cdot m^{-1}}) $ $ k/(\mathrm{A\cdot m^{-1}}) $ c $ \alpha/(\mathrm{A\cdot m^{-1}}) $ a superiority-seeking boundaries 0.5×106～1.0×106 1～50 0～10 1.0×10−6～1.0×10−4 0～20 coding boundaries 0.5×106～1.0×106 10～500 0～104 1～100 0～2×103 
下载: 导出CSV
表 2 不同磁化速率下J-A参数辨识结果及相对误差值
Table 2. J-A parameter identification results and relative error values at different magnetization rates
magnetization rate/(T·μs−1) $ {M_{\mathrm{s}}}/({\rm{A}} \cdot {{\rm{m}}^{ - 1}}) $ $ k/({\rm{A}} \cdot {{\rm{m}}^{ - 1}}) $ c $ \alpha /({\rm{A}} \cdot {{\rm{m}}^{ - 1}}) $ a $ {\rm{error}}/{\text{%}} $ 1.5 767287 39.0 5.745 6.90×10−5 0.05 6.060 2.0 757373 20.5 0.013 7×10−6 9.45 2.553 2.4 815590 12.9 0.004 5×10−6 17.60 2.552 3.3 751982 31.3 0.032 6.7×10−5 16.41 4.991
下载: 导出CSV
表 3 脉冲前沿误差及脉冲幅值的相对误差表
Table 3. Table of relative errors of pulse front error and pulse amplitude
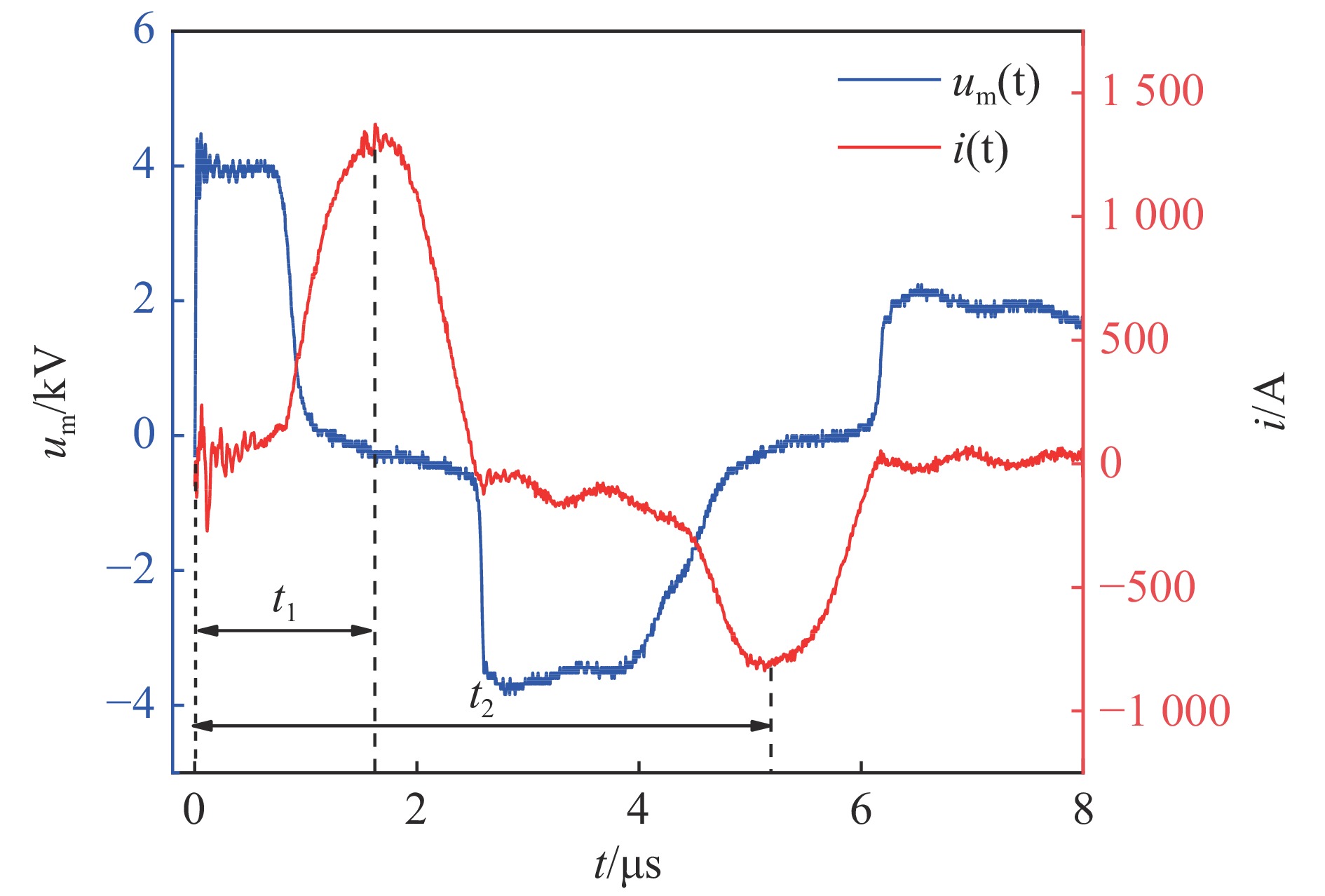
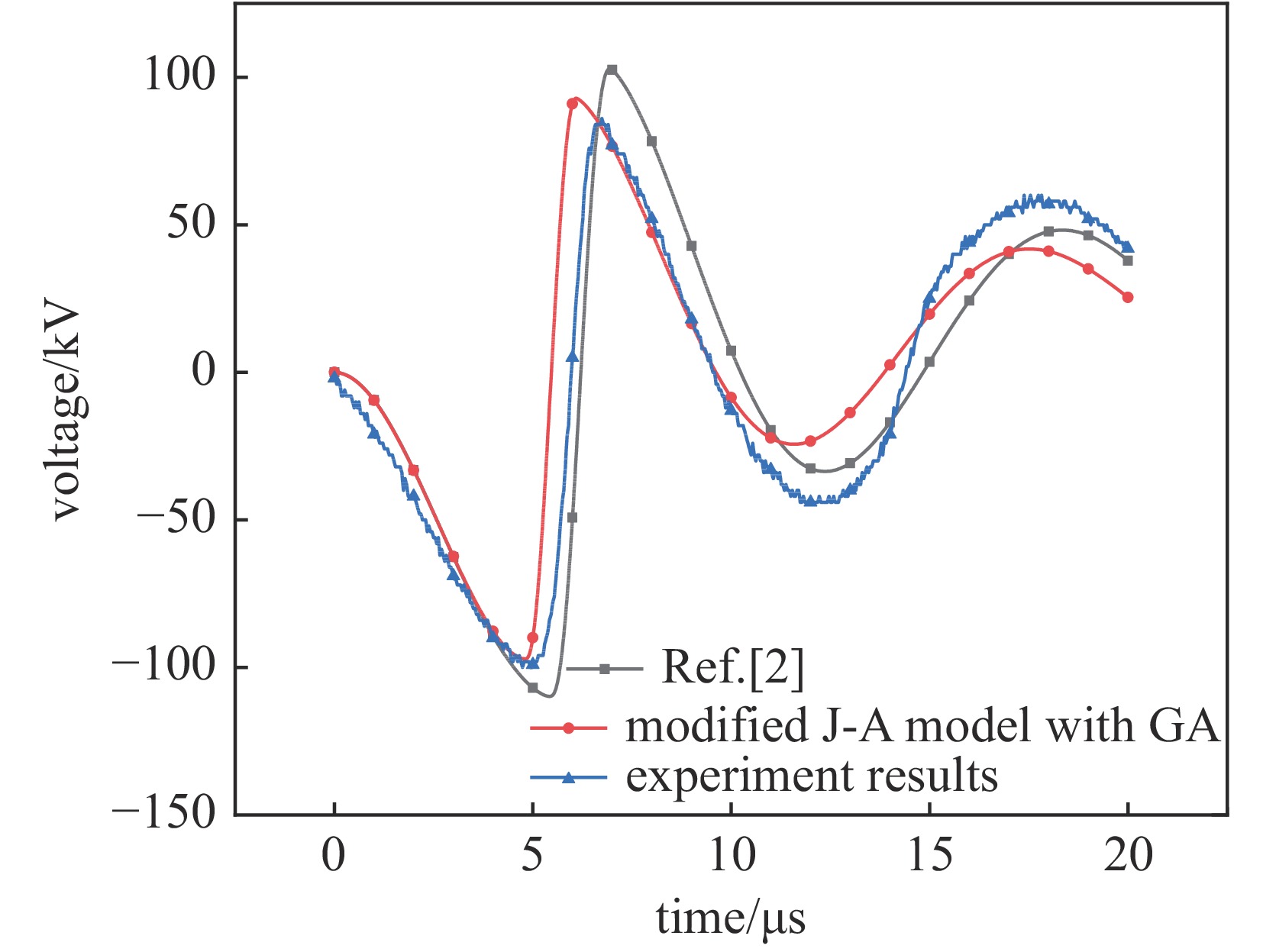
pulse front/μs pulse amplitude/kV experimental value simulation value error/% experimental value simulation value error/% modified J-A model with GA 4.967 4.807 3.33 100.028 97.199 2.91 experimental and simulation data
from Ref. [2]5.0 5.445 8.0 100 110.020 9.0
下载: 导出CSV
-
[1] 万臻博, 丁卫东, 何旭. 基于Jiles-Atherton模型的四级串联FLTD电路仿真[J]. 现代应用物理, 2022, 13:040406Wan Zhenbo, Ding Weidong, He Xu. Simulation of FLTD with a four stages in series circuit based on Jiles-Atherton model[J]. Modern Applied Physics, 2022, 13: 040406 [2] 江进波, 王佳栋, 程廷强, 等. 基于场路耦合方法的100 kV脉冲变压器设计与磁饱和特性[J]. 高电压技术, 2022, 48(12):4893-4903Jiang Jinbo, Wang Jiadong, Cheng Tingqiang, et al. Design of a 100 kV pulse transformer based on field-circuit coupling method and its magnetic saturation characteristics research[J]. High Voltage Engineering, 2022, 48(12): 4893-4903 [3] 段建东, 雷阳, 李浩, 等. 铁磁元件J-A模型的研究进展与趋势[J]. 高压电器, 2020, 56(12):16-23Duan Jiandong, Li Yang, Li Hao, et al. Review of ferromagnetic components J-A model[J]. High Voltage Apparatus, 2020, 56(12): 16-23 [4] 耿超, 王丰华, 苏磊, 等. 基于人工鱼群与蛙跳混合算法的变压器Jiles-Atherton模型参数辨识[J]. 中国电机工程学报, 2015, 35(18):4799-4807Geng Chao, Wang Fenghua, Su Lei, et al. Parameter identification of Jiles-Atherton model for transformer based on hybrid artificial fish swarm and shuffled frog leaping algorithm[J]. Proceedings of the CSEE, 2015, 35(18): 4799-4807 [5] 莫仕勋, 杨皓, 蒋坤坪, 等. 基于改进秃鹰搜索算法的变压器J-A模型参数辨识[J]. 电工电能新技术, 2022, 41(4):67-74Mo Shixun, Yang Hao, Jiang Kunping, et al. Parameter identification of transformer J-A model based on improved BES algorithm[J]. Advanced Technology of Electrical Engineering and Energy, 2022, 41(4): 67-74 [6] 李丹丹, 吴宇翔, 朱聪聪, 等. 基于麻雀搜索与遗传算法的J-A磁滞模型参数辨识方法[J]. 高电压技术, 2022, 48(10):4181-4188Li Dandan, Wu Yuxiang, Zhu Congcong, et al. Parameter identification method for J-A hysteresis model based on the sparrow search and genetic algorithm[J]. High Voltage Engineering, 2022, 48(10): 4181-4188 [7] 陈彬, 秦小彬, 唐波, 等. 基于R-L分数阶导数的动态J-A磁滞模型及其特征参数辨识算法[J]. 中国电机工程学报, 2022, 42(12):4590-4602Chen Bin, Qin Xiaobin, Tang Bo, et al. Dynamic J-A hysteresis model based on R-L fractional derivative and its characteristic parameter identification algorithm[J]. Proceedings of the CSEE, 2022, 42(12): 4590-4602 [8] 赵越, 李琳, 刘任, 等. 基于损耗统计理论的动态J-A磁滞模型[J]. 电工电能新技术, 2019, 38(5):90-96 doi: 10.12067/ATEEE1806077Zhao Yue, Li Lin, Liu Ren, et al. New dynamic hysteresis J-A model based on statistical theory of losses[J]. Advanced Technology of Electrical Engineering and Energy, 2019, 38(5): 90-96 doi: 10.12067/ATEEE1806077 [9] 王旭, 张艳丽, 唐伟, 等. 旋转磁化下逆矢量Jiles-Atherton磁滞模型改进[J]. 电工技术学报, 2018, 33(s2):257-262Wang Xu, Zhang Yanli, Tang Wei, et al. Improvement of inverse vector Jiles-Atherton hysteresis model under rotating magnetization[J]. Transactions of China Electrotechnical Society, 2018, 33(s2): 257-262 [10] 熊林, 苏建仓, 何锋, 等. 磁性材料磁滞回线模型参数的计算[J]. 真空电子技术, 2004(3):16-19 doi: 10.3969/j.issn.1002-8935.2004.03.004Xiong Lin, Su Jiancang, He Feng, et al. Calculations of hysteresis loop model parameters for magnetic materials[J]. Vacuum Electronics, 2004(3): 16-19 doi: 10.3969/j.issn.1002-8935.2004.03.004 [11] Zhang He, Liu Yi, Liu Siwei, et al. A method for reducing errors of magnetization modeling of nanocrystalline alloy cores based on modified Jiles-Atherton model[J]. Journal of Applied Physics, 2019, 125: 143901. doi: 10.1063/1.5086835 [12] Jiles D C, Atherton D L. Theory of ferromagnetic hysteresis (invited)[J]. Journal of Applied Physics, 1984, 55(6): 2115-2120. doi: 10.1063/1.333582 [13] Jiles D C, Atherton D L. Theory of the magnetisation process in ferromagnets and its application to the magnetomechanical effect[J]. Journal of Physics D:Applied Physics, 1984, 17(6): 1265-1281. doi: 10.1088/0022-3727/17/6/023 [14] Jiles D C, Atherton D L. Theory of ferromagnetic hysteresis[J]. Journal of Magnetism and Magnetic Materials, 1986, 61(1/2): 48-60. [15] 李贞, 李庆民, 李长云, 等. J-A磁化建模理论的质疑与修正方法研究[J]. 中国电机工程学报, 2011, 31(3):124-131Li Zhen, Li Qingmin, Li Changyun, et al. Queries on the J-A modeling theory of the magnetization process in ferromagnets and proposed correction method[J]. Proceedings of the CSEE, 2011, 31(3): 124-131 [16] Ma Yilin, Wang Enlong, Yang Huan, et al. Reconsideration of nonphysical solution in Jiles–Atherton model for real-time hysteresis estimation[J]. IEEE Transactions on Magnetics, 2022, 58: 7300509. [17] Liu Yi, Han Yibo, Liu Siwei, et al. Loss and permeability characterization of Fe-based nanocrystalline cores for pulsed power magnetic applications[C]//2014 IEEE International Power Modulator and High Voltage Conference (IPMHVC). 2014: 595-598. [18] 江进波, 程廷强, 黄国良, 等. 铁基纳米晶磁芯的脉冲磁化特性测量及其在磁开关中的应用[J]. 强激光与粒子束, 2023, 35:055004 doi: 10.11884/HPLPB202335.220304Jiang Jinbo, Cheng Tingqiang, Huang Guoliang, et al. Pulse magnetic properties measurement of Fe-based nanocrystalline cores and its application in magnetic switches[J]. High Power Laser and Particle Beams, 2023, 35: 055004 doi: 10.11884/HPLPB202335.220304 [19] 刘力卿, 何思名, 冯军基, 等. 一种快速高鲁棒性变压器铁心Jiles-Atherton磁滞模型参数辨识方法[J]. 高压电器, 2020, 56(1):55-60Liu Liqing, He Siming, Feng Junji, et al. Fast and robust parameter identification method for Jiles-Atherton hysteresis model of transformer core[J]. High Voltage Apparatus, 2020, 56(1): 55-60 -
点击查看大图
图(10) / 表(3)
计量
- 文章访问数: 219
- HTML全文浏览量: 94
- PDF下载量: 36
- 被引次数: 0
