临界事故报警系统的相似性

徐源; 江世航; 杨海峰; 易璇; 邵增

doi:10.11884/HPLPB202436.230368

临界事故报警系统的相似性

doi: 10.11884/HPLPB202436.230368

徐源^1,,
江世航²,
杨海峰^1, ,,
易璇¹,
邵增¹

1.
中国核电工程有限公司，北京 100840
2.
清华大学工程物理系，北京 100084

详细信息

作者简介:
徐　源，xuyuan@cnpe.cc

通讯作者:
杨海峰，yanghf@cnpe.cc。

中图分类号: TL731
计量
- 文章访问数: 257
- HTML全文浏览量: 111
- PDF下载量: 21
- 被引次数: 0
出版历程
- 收稿日期: 2023-10-19
- 修回日期: 2024-05-08
- 录用日期: 2024-05-08
- 网络出版日期: 2024-05-16
- 刊出日期: 2024-07-04

Similarity analysis applied to nuclear criticality accident alarm systems

1.
China Nuclear Power Engineering Co. Ltd, Beijing 100840, China
2.
Department of Engineering Physics, Tsinghua University, Beijing 100084, China

摘要

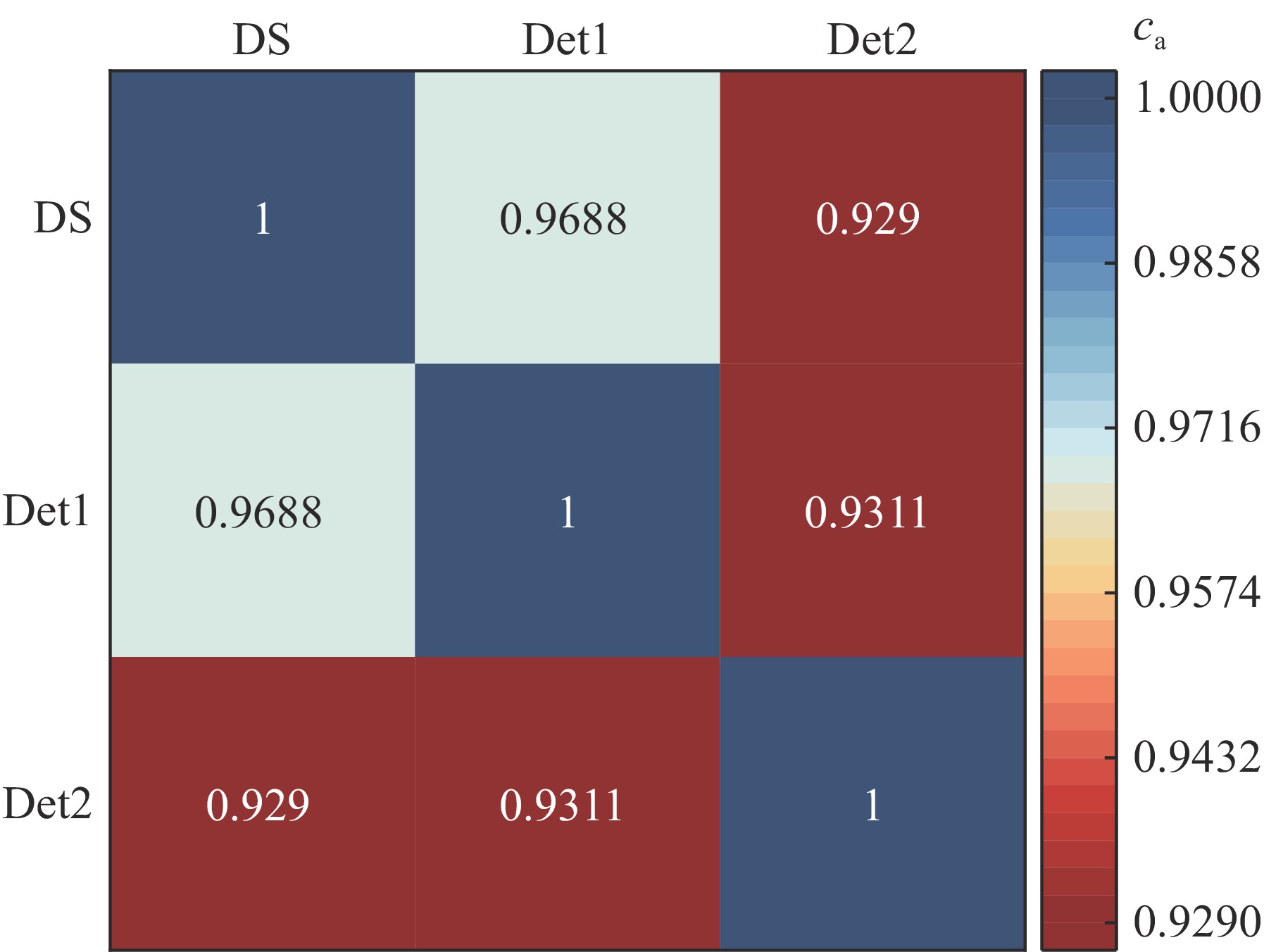
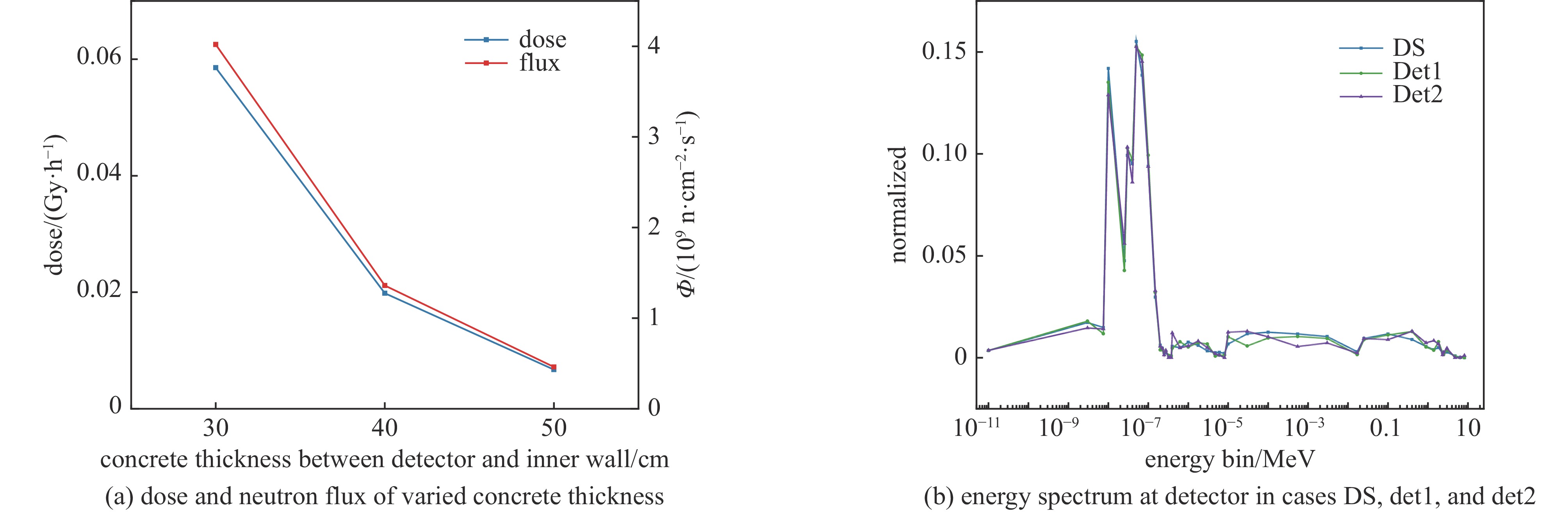
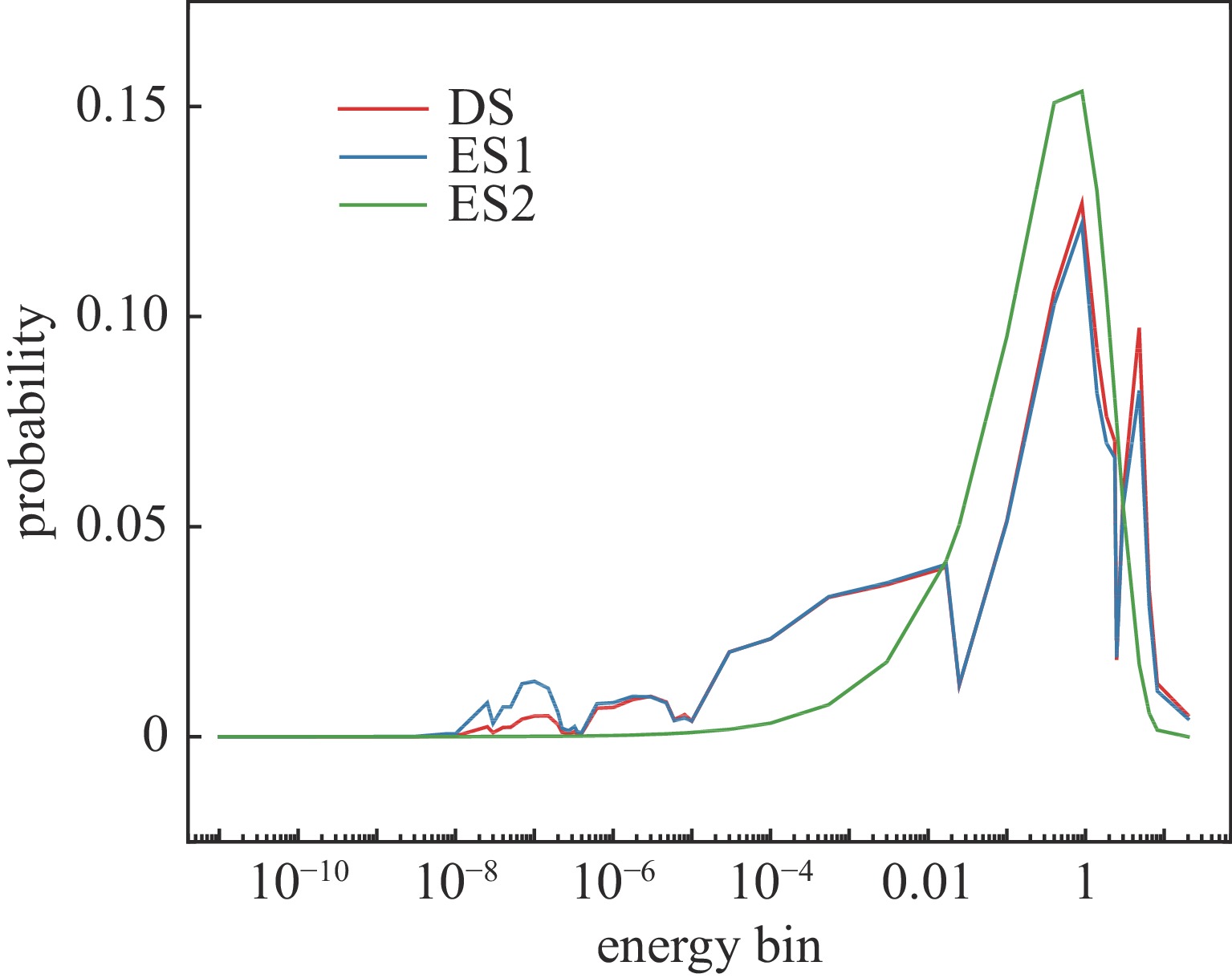
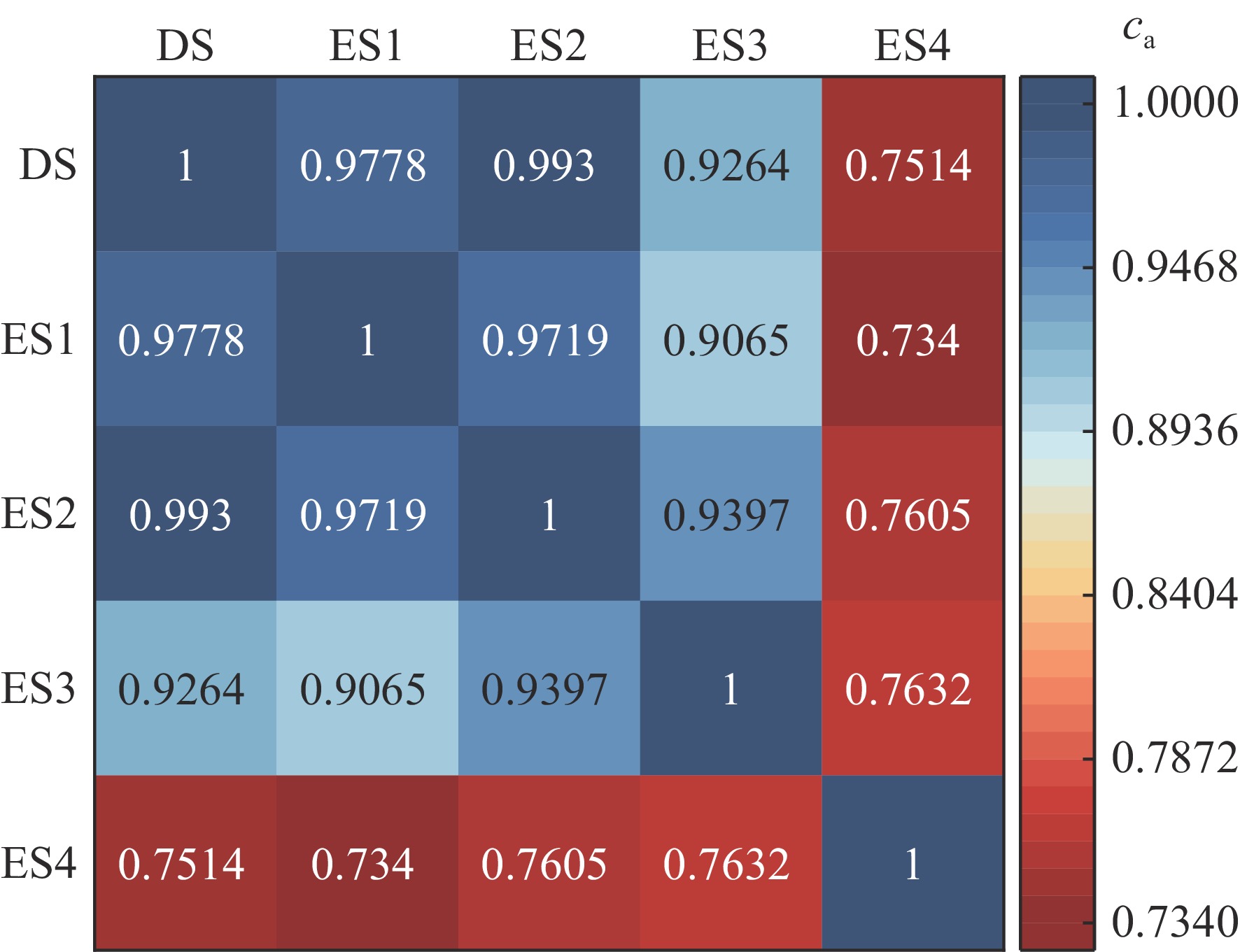
摘要: 为了确定用于场所监测的临界事故报警系统合适的报警阈值，需选用相似的基准实验进行验证。根据设备室临界事故报警系统的特征，构建了简易模型和具有代表性的包含多个设备的虚拟设备室模型。针对固定源问题，在蒙卡程序（RMC）中实现了基于微分算符抽样法计算敏感性系数的功能。随后，运用敏感性和不确定度分析方法对系统间的相似性进行了研究，并深入分析了影响相似性的因素。计算分析结果显示，对于简易模型，源项能谱和混凝土材料对系统间的相似性有较大影响，探测器与内侧墙面之间的混凝土厚度对相似性有一定影响，而源项的几何位置对相似性的影响较小，乏燃料成分对相似性的影响可以忽略不计。根据本文提出的相似性分析流程进行计算得出，简易模型与虚拟设备室模型的相似性较高，基于简易模型的研究结论适用于虚拟设备室模型，可为工程上的临界报警系统相似性研究提供参考。
- 固定源相似性 /
- 敏感性分析 /
- 不确定度 /
- 临界事故报警系统
Abstract: To determine the alarm threshold for criticality accident alarm systems (CAASs) used in facility monitoring, it is necessary to select appropriate benchmark experiments for validation. This paper constructs a simplified model and a representative virtual equipment room model, taking into consideration the characteristics of CAASs in the equipment room. The functionality of calculating sensitivity coefficients using the differential operator sampling approach in the Monte Carlo code RMC was implemented to solve the fixed source problem. Following that, a sensitivity and uncertainty analysis was conducted to examine the similarities between systems and explore the factors influencing them. The results indicate that the neutron source term spectrum and the concrete material significantly affect the similarity between systems. Additionally, the thickness of the concrete between the detector and the inner wall has a moderate influence on similarity, whereas the geometric position of the source term has a negligible impact. The impact of the spent fuel composition on similarity can be neglected. Based on the similarity analysis procedure proposed in this study, it is concluded that the simplified model exhibits a relatively high similarity to the virtual equipment room model. Hence, the research conclusions based on the simplified model are applicable to the virtual equipment room model, offering valuable insights for similarity studies of CAASs in engineering.
- fixed source system similarity /
- sensitivity analysis /
- uncertainty /
- criticality accident alarm system

HTML全文

图 1 小模型DS算例在z=0 cm处的切面图

Figure 1. XY view of case DS at z=0 cm

下载: 全尺寸图片幻灯片

图 2 算例Geo11-111和Geo21-211中子源位置示意图

Figure 2. XY view of varied position of neutron source for cases Geo11-111 and Geo21-211

下载: 全尺寸图片幻灯片

图 3 算例GeoH1-5中子源位置示意图

Figure 3. XZ view of varied position of neutron source for cases GeoH1-5

下载: 全尺寸图片幻灯片

图 4 算例Geo11-111 Geo21-211之间的相似性系数热图

Figure 4. Heat map of similarity coefficients between cases Geo11-111 Geo21-211

下载: 全尺寸图片幻灯片

图 5 算例GeoH1-5之间的相似性系数热图

Figure 5. Heat map of similarity coefficients between cases GeoH1-5

下载: 全尺寸图片幻灯片

图 6 算例DS, Det1, Det2之间的相似性系数热图

Figure 6. Heat map of similarity coefficients between cases DS, Det1, and Det2

下载: 全尺寸图片幻灯片

图 7 算例DS, Det1, Det2探测位置处的计算结果

Figure 7. Results of detector in cases DS, Det1, and Det2

下载: 全尺寸图片幻灯片

图 8 算例DS, ES1, ES2的中子源能谱对比图

Figure 8. Energy spectrum of neutron source in cases DS, ES1, and ES2

下载: 全尺寸图片幻灯片

图 9 算例DS, ES1-4之间的相似性系数热图

Figure 9. Heat map of similarity coefficients between cases DS and ES1-4

下载: 全尺寸图片幻灯片

图 10 算例DS, M1-4之间的相似性系数热图

Figure 10. Heat map of similarity coefficients between cases DS and M1-4

下载: 全尺寸图片幻灯片

图 11 虚拟设备室切面图

Figure 11. XY view of the virtual equipment room model

下载: 全尺寸图片幻灯片

图 12 小模型DS算例与虚拟设备室模型之间的相似性系数

Figure 12. Similarity coefficient between cases DS and virtual equipment room model

下载: 全尺寸图片幻灯片

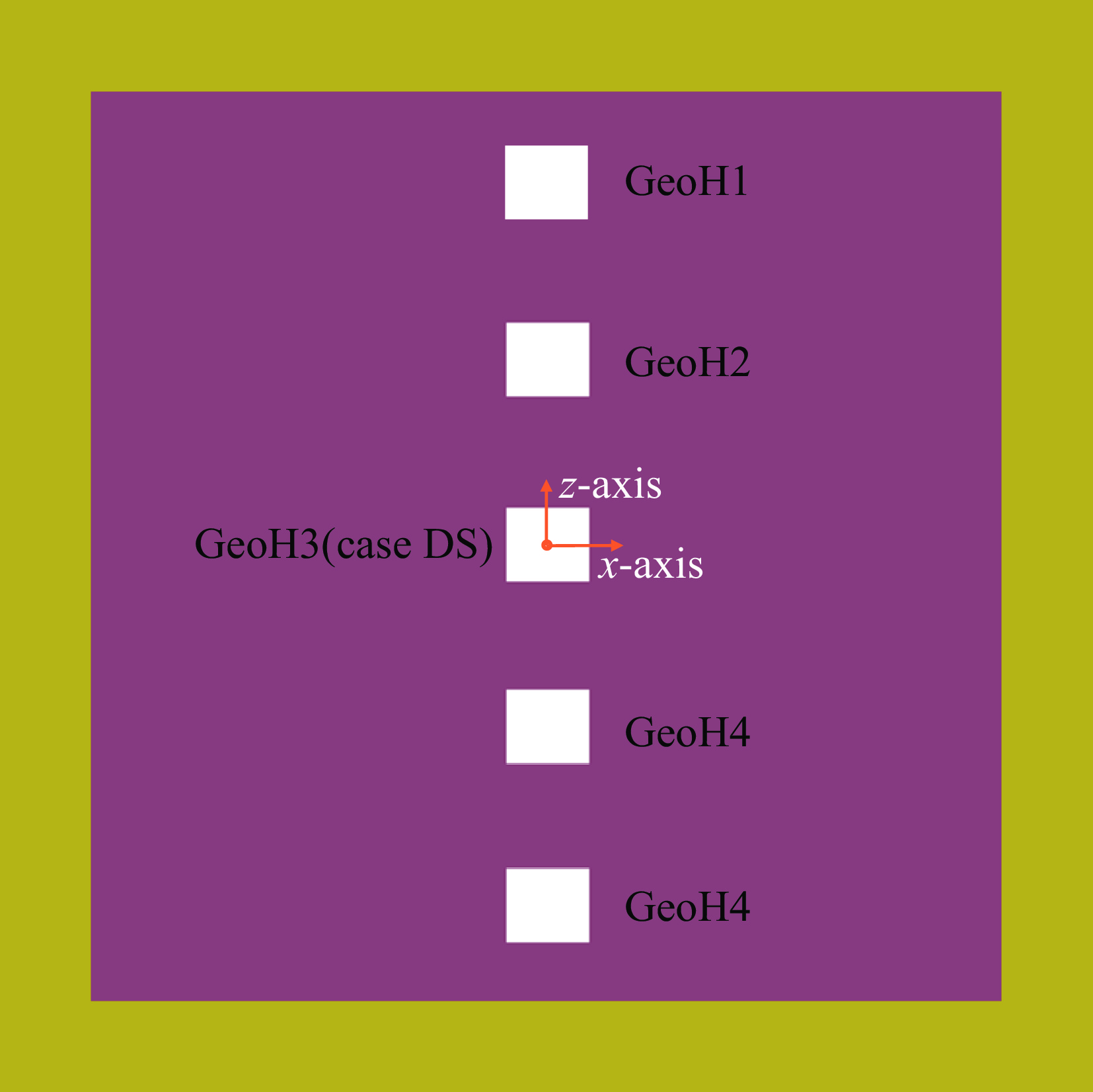
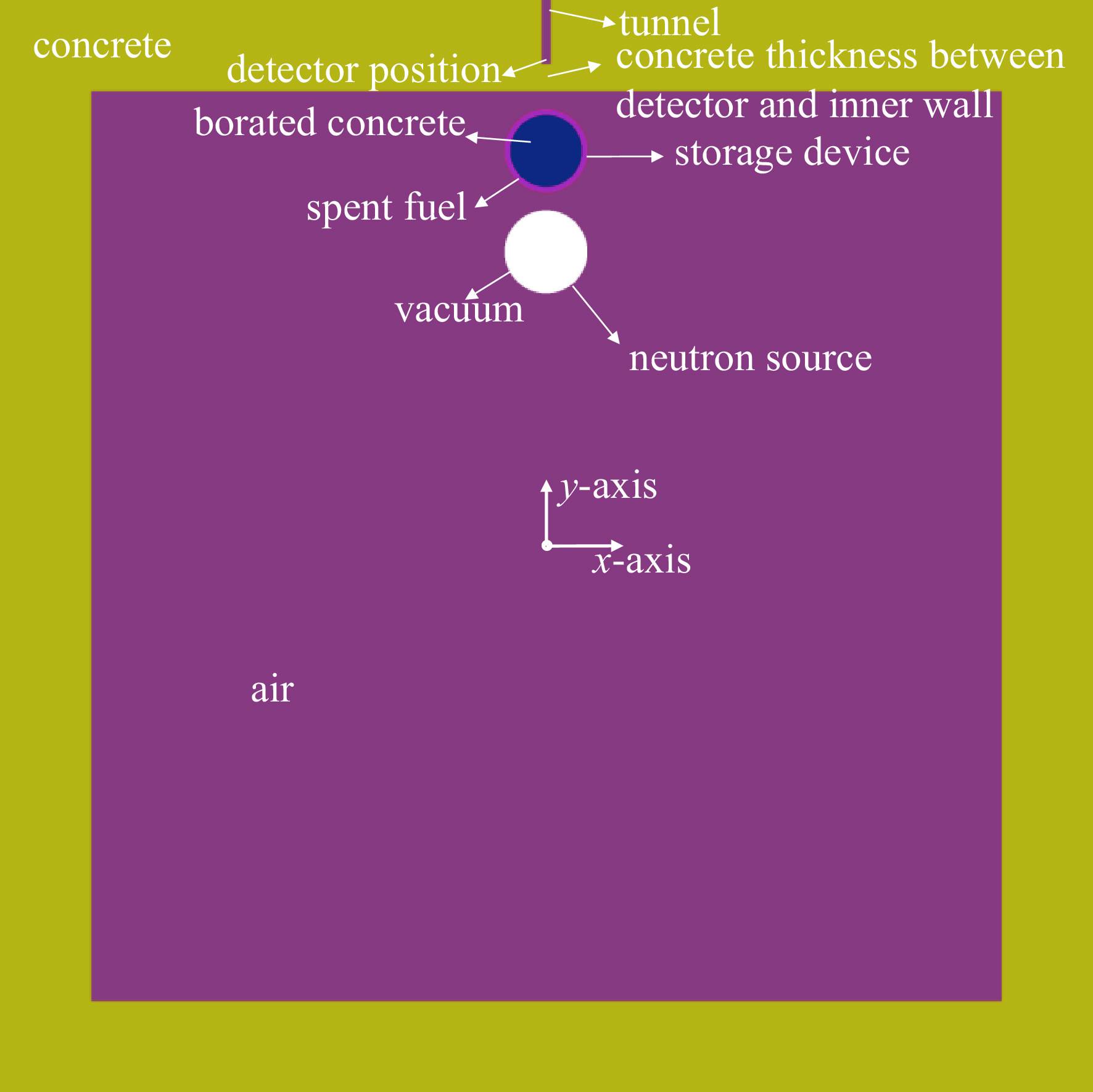
表 1 小模型DS算例尺寸数据

Table 1. Dimensions of case DS

	x-coordinate range/cm	y-coordinate range/cm	z-coordinate range/cm
inside of wall	−500～+500	−500～+500	−500～+500
outside of wall	−600～+600	−600～+600	−600～+600
tunnel	−5～+5	530～600	−5～+5
detector	−5～+5	530～540	−5～+5

下载: 导出CSV

表 2 小模型DS算例设备与中子源尺寸数据

Table 2. Dimensions of the storage device and the neutron source for case DS

	x-coordinate of axis/cm	y-coordinate of axis/cm	z-coordinate range/cm	radius/cm
storage device	0	434.5	−40.5～+40.5	45.5
neutron source	0	323.5	−40.5～+40.5	45.5

下载: 导出CSV

表 3 虚拟设备室整体尺寸

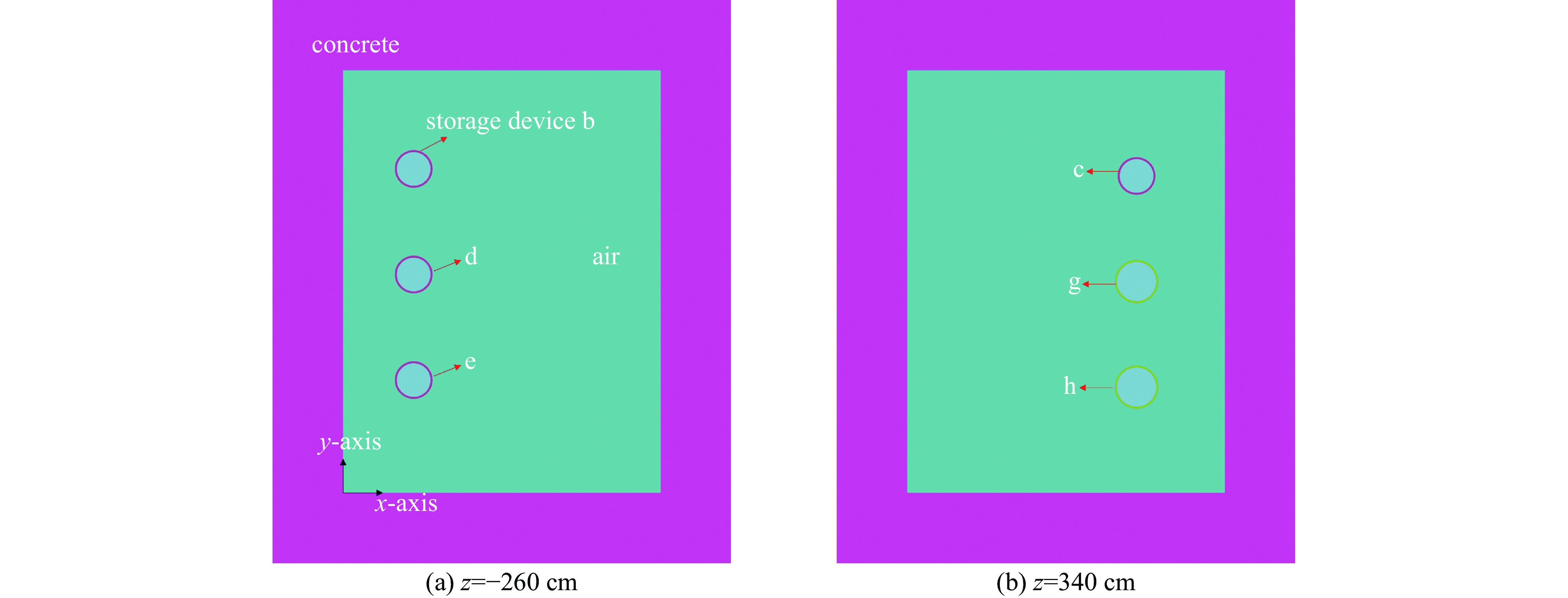
Table 3. Dimensions of the virtual equipment room model

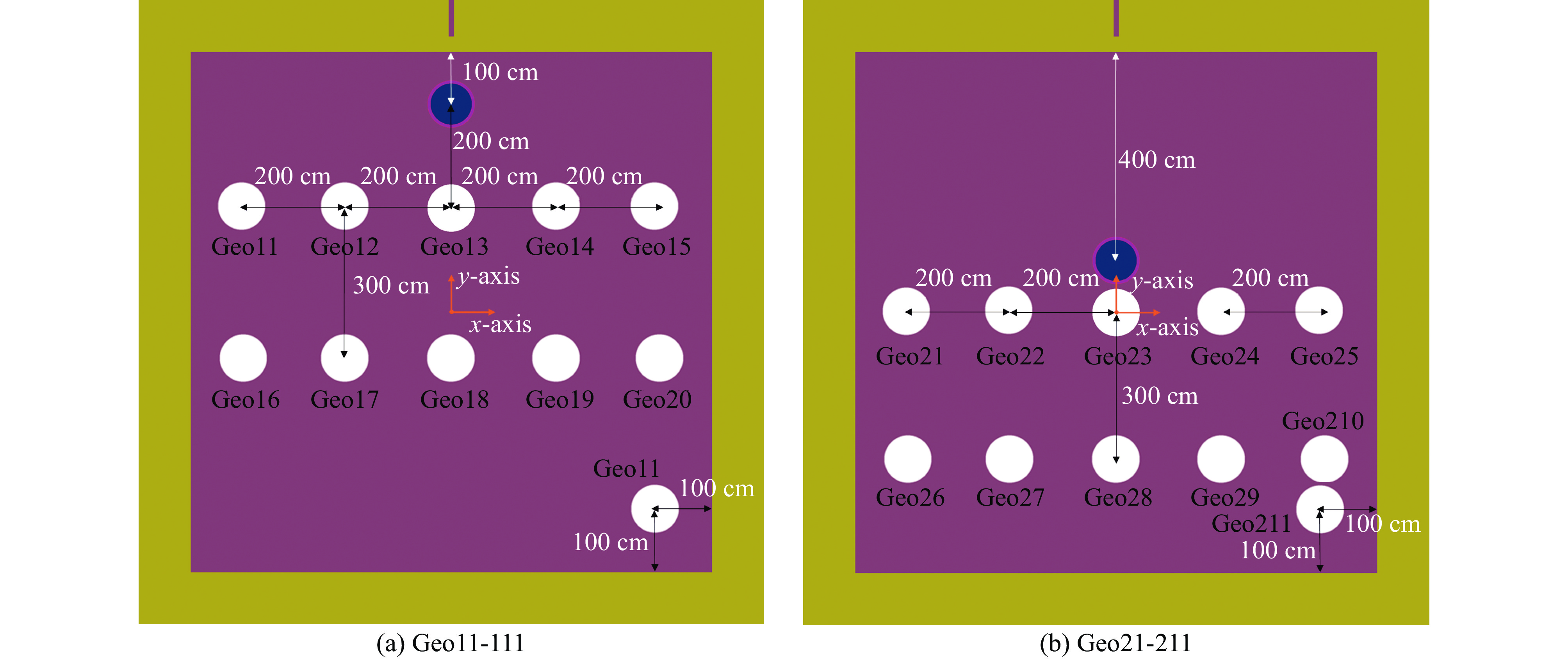
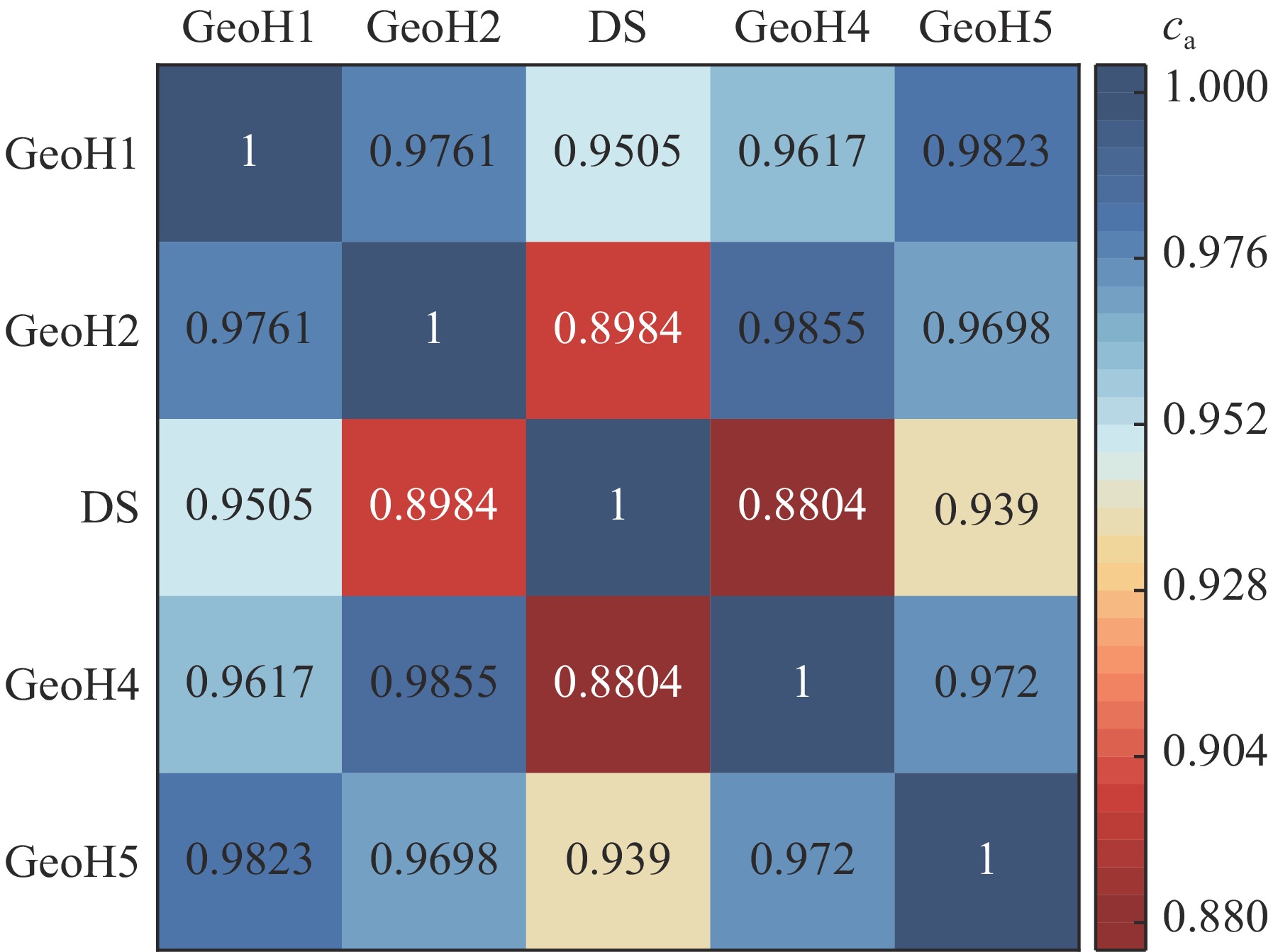
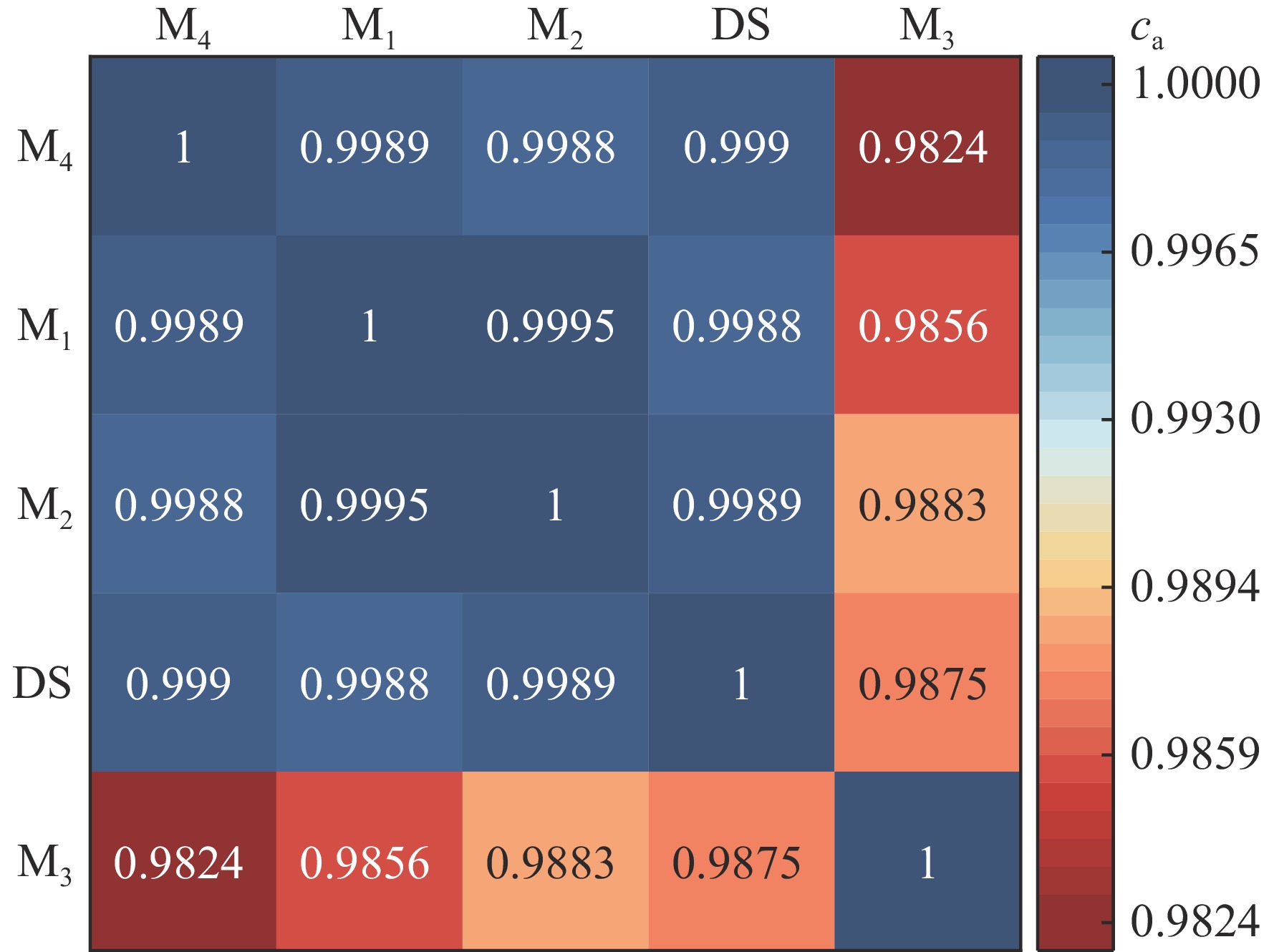
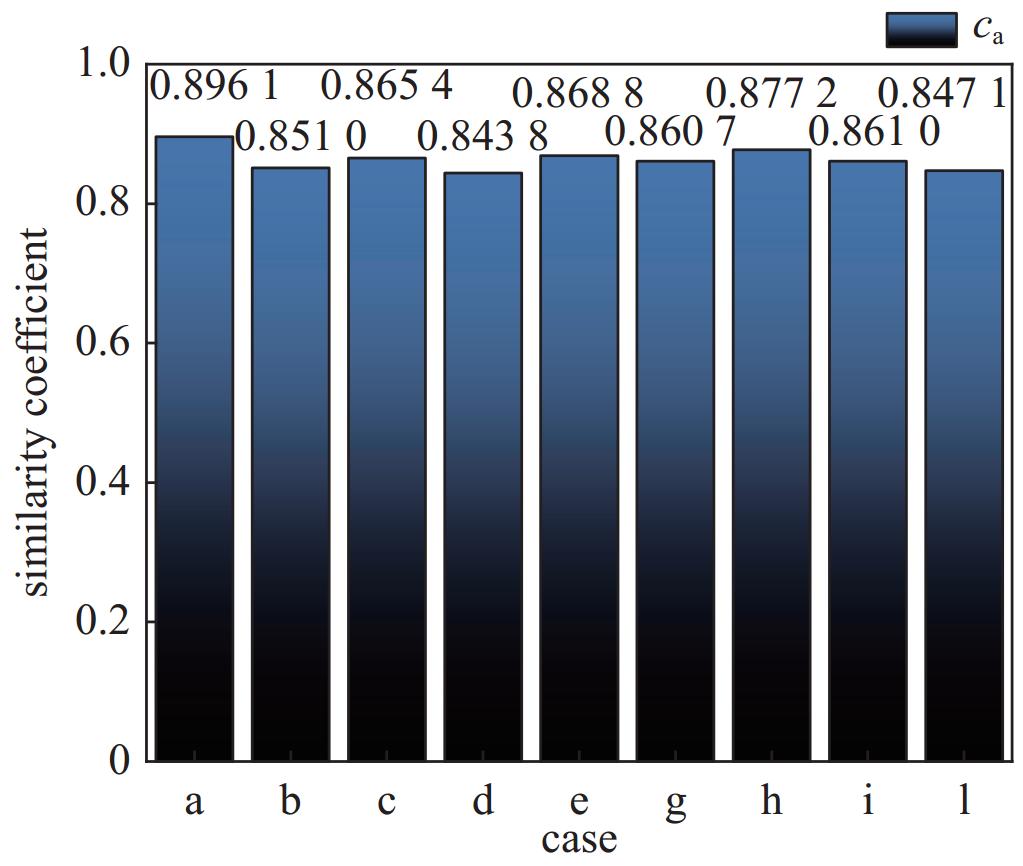
	x-coordinate range/cm	y-coordinate range/cm	z-coordinate range/cm
inside of wall	0～+675	0～+900	−600～+600
outside of wall	−150～+825	0～+1050	−800～+750

下载: 导出CSV

表 4 小模型DS算例与虚拟设备室各算例之间的相似性系数贡献

Table 4. Most important contributions from varied reactions to similarity coefficients between cases DS and the virtual equipment room model

nuclide-reaction	contributions to similarity coefficient
nuclide-reaction	a	b	c	d	e	g	h	i	l
H-inelastic scattering	4.71×10⁻¹	4.17×10⁻¹	4.16×10⁻¹	4.03×10⁻¹	4.31×10⁻¹	4.15×10⁻¹	4.50×10⁻¹	4.15×10⁻¹	4.01×10⁻¹
²⁸Si-(n, γ)	2.58×10⁻¹	2.64×10⁻¹	2.72×10⁻¹	2.69×10⁻¹	2.67×10⁻¹	2.71×10⁻¹	2.60×10⁻¹	2.72×10⁻¹	2.70×10⁻¹
⁵⁸Ni-(n, γ)	1.55×10⁻¹	1.59×10⁻¹	1.63×10⁻¹	1.61×10⁻¹	1.60×10⁻¹	1.62×10⁻¹	1.56×10⁻¹	1.64×10⁻¹	1.62×10⁻¹
¹⁶O-elastic scattering	−3.92×10⁻²	−4.23×10⁻²	−4.16×10⁻²	−4.38×10⁻²	−4.17×10⁻²	−4.18×10⁻²	−4.09×10⁻²	−4.40×10⁻²	−4.15×10⁻²
³⁹K-(n, γ)	2.01×10⁻²	2.06×10⁻²	2.12×10⁻²	2.10×10⁻²	2.08×10⁻²	2.11×10⁻²	2.03×10⁻²	2.12×10⁻²	2.11×10⁻²
⁴⁰Ca-(n, γ)	8.28×10⁻³	8.47×10⁻³	8.73×10⁻³	8.62×10⁻³	8.56×10⁻³	8.67×10⁻³	8.34×10⁻³	8.73×10⁻³	8.67×10⁻³
H-(n, γ)	7.97×10⁻³	8.14×10⁻³	8.39×10⁻³	8.29×10⁻³	8.22×10⁻³	8.34×10⁻³	8.02×10⁻³	8.40×10⁻³	8.33×10⁻³
H-elastic scattering	5.33×10⁻³	5.93×10⁻³	5.91×10⁻³	5.95×10⁻³	5.65×10⁻³	5.83×10⁻³	5.67×10⁻³	5.94×10⁻³	6.22×10⁻³
²⁷Al-(n, γ)	4.52×10⁻³	4.62×10⁻³	4.77×10⁻³	4.71×10⁻³	4.67×10⁻³	4.74×10⁻³	4.55×10⁻³	4.77×10⁻³	4.73×10⁻³

下载: 导出CSV

参考文献(10)

[1]	GB/T15146.9-1994, 反应堆外易裂变材料的核临界安全核临界事故探测与报警系统的性能及检验要求[S] GB/T15146.9-1994, Nuclear criticality safety for fissile materials outside reactor-Performance and testing requirements for nuclear criticality detection and alarm systems[S]
[2]	丘意书. 基于RMC的核数据敏感性与燃耗不确定度分析方法研究[D]. 北京: 清华大学, 2017 Qiu Yishu. Nuclear data sensitivity and uncertainty analysis in the burnup calculation based on RMC code[D]. Beijing: Tsinghua University, 2017
[3]	Broadhead B L, Hopper C M, Childs R L, et al. Sensitivity and uncertainty analyses applied to criticality safety validation, methods development. Volume 1[R]. Oak Ridge National Lab., 1999.
[4]	Marshall W J, Clarity J B, Rearden B T. A review of TSUNAMI applications[J]. Transactions of the American Nuclear Society, 2020, 123(1): 795-798.
[5]	Zheng Youqi, Qiao Liang, Wan Chenghui, et al. Sensitivity analysis and similarity evaluation of sodium-cooled fast reactor in large size[J]. Annals of Nuclear Energy, 2019, 125: 283-290. doi: 10.1016/j.anucene.2018.11.026
[6]	Ning Tong, Zhou Qi, Chen Xiaoliang, et al. Application of similarity analysis method in zero-power experimental validation[J]. The European Physical Journal Conferences, 2020, 239: 17017. doi: 10.1051/epjconf/202023917017
[7]	Wang Kan, Li Zeguang, She Ding, et al. RMC—A Monte Carlo code for reactor core analysis[J]. Annals of Nuclear Energy, 2015, 82: 121-129. doi: 10.1016/j.anucene.2014.08.048
[8]	Rief H. Generalized Monte Carlo perturbation algorithms for correlated sampling and a second-order Taylor series approach[J]. Annals of Nuclear Energy, 1984, 11(9): 455-476. doi: 10.1016/0306-4549(84)90064-1
[9]	Choi S H, Shim H J, Kim C H. Development of generalized perturbation theory algorithms for Monte Carlo eigenvalue calculations[J]. Nuclear Science and Engineering, 2018, 189(2): 171-187. doi: 10.1080/00295639.2017.1388089
[10]	江世航, 徐源, 王侃, 等. 基于RMC的蒙卡屏蔽计算敏感性分析方法[C]//第十九届反应堆数值计算与粒子输运学术会议暨2023年反应堆物理会议 Jiang Shihang, Xu Yuan, Wang Kan, et al. RMC-based Monte Carlo shielding computation sensitivity analysis method[C]//CORPHY2022