Quantification of calculated effective multiplication factor uncertainty caused by nuclear data in research reactor
-
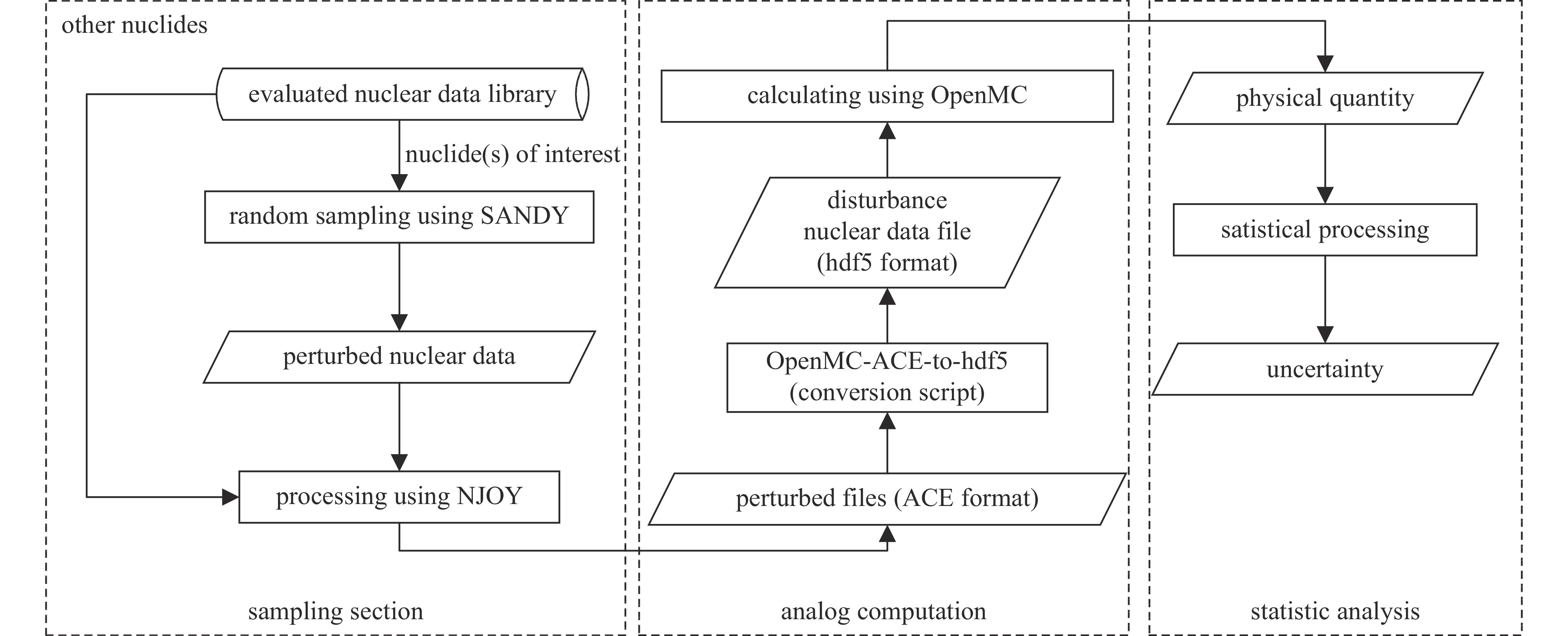
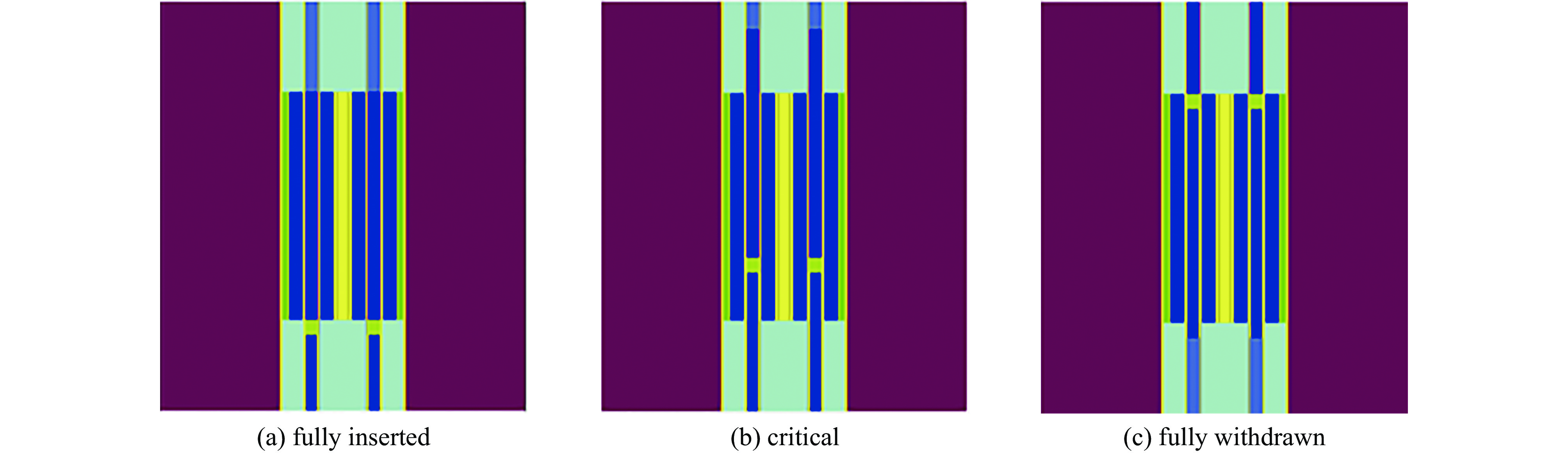
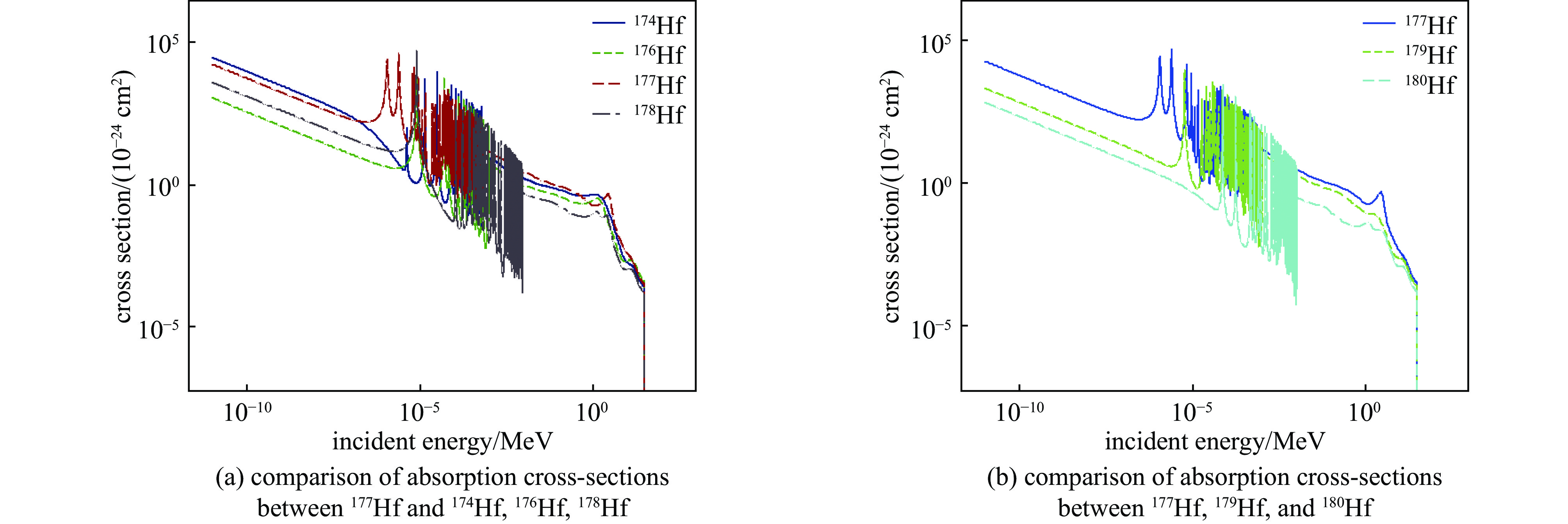
摘要: 为了深入研究核数据不确定度对JRR-3M研究堆有效增殖因子计算的影响，建立了一套基于蒙特卡罗法的核数据不确定度量化流程。具体方法为：使用核数据扰动软件SANDY扰动目标核素的重要反应道生成扰动文件，再通过核数据加工软件NJOY对扰动文件进行处理，最终利用核反应堆物理模拟软件OpenMC进行蒙特卡罗模拟。针对JRR-3M研究堆的控制棒全插、反应堆临界、控制棒全拔三种运行工况，对多个关键核素（如235U、238U、Hf等）的核数据不确定度给有效增殖因子计算带来的影响进行了详细分析。研究结果表明，177Hf、235U、1H、27Al的核数据不确定度对JRR-3M有效增殖因子具有显著影响。临界、控制棒全插和控制棒全提这3种工况下，核数据不确定引起的有效增殖因子总不确定度分别为660.8×10−5、588.5×10−5、708.4×10−5。在各个工况下，235U的次级粒子能量分布的影响都是最大的。研究发现，对以铪为主要组成材料的控制棒内，只有177Hf的核数据不确定度起主要影响。Abstract: To delve into the impact of nuclear data uncertainty on the effective multiplication factor calculation for the JRR-3M research reactor, this study established a nuclear data uncertainty quantification process based on SANDY. The specific methodology involved perturbing important reaction pathways of the target nuclides with SANDY to generate perturbation files, processing these files with NJOY, and ultimately utilizing OpenMC for Monte Carlo simulations. The influence on the effective multiplication factor due to several key nuclides (such as 235U, 238U, Hf, etc.) data uncertainty was calculated and analysed for three operational conditions of the JRR-3M research reactor. For critical, control rods fully inserted and control rods fully withdrawn conditions, total effective multiplication factor uncertainties are 660.8×10−5, 588.5×10−5 and 708.4×10−5, respectively. In all operational conditions, the impact of the fission release neutron energy distribution of 235U is the most notable. The study reveals that within hafnium control rods only the nuclear data uncertainty of 177Hf plays a major role.
-
图 4 三种工况下的堆芯示意图
Figure 4. Core cross-sections under three operating conditions of control rods
图 6 TENDL-2021库中铪的吸收截面对比
Figure 6. Comparison of absorption cross-sections of hafnium in TENDL-2021 library
表 1 钠的单群弹性散射截面扰动结果对比
Table 1. Comparison of disturbance results of single group elastic scattering cross section of sodium
下载: 导出CSV
表 2 JRR-3M三种工况下各核素对keff的不确定度贡献
Table 2. Contribution of uncertainty of each nuclide under three working conditions
working condition keff uncertainty caused by
fuel nuclides/10−5uncertainty caused by
coolant and moderator/10−5uncertainty caused by
control rod material/10−5total/10−5 27Al 238U 235U total 1H 2H 16O 9Be total 174Hf 176Hf 177Hf 178Hf 179Hf 180Hf total critical condition 1.00457 ±0.00008 309.5 67.6 417.0 523.7 346.6 41.6 107.1 59.9 370.0 15.0 15.1 154.7 15.4 22.9 17.3 156.5 660.8 control rod
fully inserted1.00457 ±0.00008 247.5 57.5 309.8 400.7 250.0 46.1 96.4 60.2 278.5 13.9 17.3 324.7 17.6 40.1 20.9 329.1 588.5 control rod
fully withdrawn1.00457 ±0.00008 366.7 83.2 454.5 589.9 367.4 44.3 100.4 75.0 390.7 13.2 13.8 13.8 13.5 14.0 14.3 33.7 708.4
下载: 导出CSV
表 3 各工况下各反应道的不确定度量化结果
Table 3. Quantitative results of uncertainty for each reaction channel under different operating conditions
(10−5) nuclide reaction channel critical condition control rod fully inserted control rod fully withdrawn 235U capture 181.5 154.4 237.0 fission 115.9 99.5 132.4 inelastic scattering 8.3 7.2 8.9 elastic scattering 8.9 8.7 8.2 prompt multiplicity 131.6 116.8 163.9 energy distribution 331.8 220.1 325.4 238U capture 51.9 46.2 68.8 fission 8.3 7.8 8.2 inelastic scattering 36.9 27.1 39.7 elastic scattering 17.0 15.0 20.0 prompt multiplicity 10.1 9.6 9.4 energy distribution 7.8 8.0 8.0 27Al capture 168.3 143.6 219.0 elastic scattering 130.9 98.3 127.1 inelastic scattering 224.3 176.0 265.3 9Be elastic scattering 42.5 42.8 52.8 inelastic scattering 42.2 42.3 53.2 16O elastic scattering 106.7 96.1 100.0 capture 8.8 7.6 8.8 1H elastic scattering 188.2 136.6 184.3 capture 291.1 209.4 317.8 2H elastic scattering 40.6 45.2 43.6 capture 9.2 9.0 7.9 174Hf capture 8.8 8.3 7.6 elastic scattering 8.2 7.5 7.7 inelastic scattering 8.9 8.2 7.6 176Hf capture 9.5 13.3 8.0 elastic scattering 8.4 7.8 8.0 inelastic scattering 8.2 7.8 7.8 177Hf capture 154.0 323.9 8.3 elastic scattering 12.1 21.6 7.7 inelastic scattering 8.4 7.7 7.9 178Hf capture 9.2 13.4 7.6 elastic scattering 8.9 8.1 8.0 inelastic scattering 8.6 8.0 7.8 179Hf capture 19.6 38.3 8.3 elastic scattering 8.4 9.2 8.0 inelastic scattering 8.3 7.4 7.9 180Hf capture 12.3 17.0 8.3 elastic scattering 8.9 8.8 8.4 inelastic scattering 8.3 8.4 8.1
下载: 导出CSV
-
[1] Zhu Ting, Vasiliev A, Ferroukhi H, et al. Testing the sampling-based NUSS-RF tool for the nuclear data–related global sensitivity analysis with Monte Carlo neutronics calculations[J]. Nuclear Science and Engineering, 2016, 184(1): 69-83. doi: 10.13182/NSE14-142 [2] 万承辉, 曹良志, 吴宏春, 等. 基于抽样方法的特征值不确定度分析[J]. 原子能科学技术, 2015, 49(11):1954-1960 doi: 10.7538/yzk.2015.49.11.1954Wan Chenghui, Cao Liangzhi, Wu Hongchun, et al. Eigenvalue uncertainty analysis based on statistical sampling method[J]. Atomic Energy Science and Technology, 2015, 49(11): 1954-1960 doi: 10.7538/yzk.2015.49.11.1954 [3] Fiorito L, Žerovnik G, Stankovskiy A, et al. Nuclear data uncertainty propagation to integral responses using SANDY[J]. Annals of Nuclear Energy, 2017, 101: 359-366. doi: 10.1016/j.anucene.2016.11.026 [4] Griseri M, Fiorito L, Stankovskiy A, et al. Nuclear data uncertainty propagation on a sodium fast reactor[J]. Nuclear Engineering and Design, 2017, 324: 122-130. doi: 10.1016/j.nucengdes.2017.08.018 [5] 强胜龙, 尹强, 芦韡, 等. 秦山二期堆芯临界计算中核数据的敏感性分析[J]. 强激光与粒子束, 2017, 29:036004 doi: 10.11884/HPLPB201729.160433Qiang Shenglong, Yin Qiang, Lu Wei, et al. Sensitivity analysis of nuclear data in core critical calculation of Qinshan Ⅱ[J]. High Power Laser and Particle Beams, 2017, 29: 036004 doi: 10.11884/HPLPB201729.160433 [6] Iwamoto H, Stankovskiy A, Fiorito L, et al. Monte Carlo uncertainty quantification of the effective delayed neutron fraction[J]. Journal of Nuclear Science and Technology, 2018, 55(5): 539-547. doi: 10.1080/00223131.2017.1416691 [7] Park J H, Pereslavtsev P, Konobeev A, et al. Statistical analysis of tritium breeding ratio deviations in the DEMO due to nuclear data uncertainties[J]. Applied Sciences, 2021, 11: 5234. doi: 10.3390/app11115234 [8] 胡泽华, 叶涛, 刘雄国, 等. 抽样法与灵敏度法keff不确定度量化[J]. 物理学报, 2017, 66:012801 doi: 10.7498/aps.66.012801Hu Zehua, Ye Tao, Liu Xiongguo, et al. Uncertainty quantification in the calculation of keff using sensitity and stochastic sampling method[J]. Acta Physica Sinica, 2017, 66: 012801 doi: 10.7498/aps.66.012801 [9] 吴屈, 余健开, 李万林, 等. 基于不同ENDF/B的ACE格式库参数制作与初步检验(英文)[J]. 强激光与粒子束, 2017, 29:026004 doi: 10.11884/HPLPB201729.160332Wu Qu, Yu Jiankai, Li Wanlin, et al. Parameter making and preliminary test of ACE format libraries based on different ENDF/B[J]. High Power Laser and Particle Beams, 2017, 29: 026004 doi: 10.11884/HPLPB201729.160332 [10] MacFarlane R E, Muir D W. The NJOY nuclear data processing system Version 91[R]. Los Alamos: Los Alamos National Lab, 1994. [11] Ma Jimin, Wang Guanbo, Yuan Shu, et al. An improved assembly homogenization approach for plate-type research reactor[J]. Annals of Nuclear Energy, 2015, 85: 1003-1013. doi: 10.1016/j.anucene.2015.07.018 [12] 戴涛, 黄洪文, 马纪敏. 基于RELAP5的池式研究堆自然循环瞬态计算[J]. 强激光与粒子束, 2018, 30:086001 doi: 10.11884/HPLPB201830.180009Dai Tao, Huang Hongwen, Ma Jimin. Transient calculation of natural circulation for pool-type research reactor[J]. High Power Laser and Particle Beams, 2018, 30: 086001) doi: 10.11884/HPLPB201830.180009 [13] 胡继峰, 王小鹤, 李文江, 等. 熔盐实验堆核数据引起反应性参数不确定度分析[J]. 核技术, 2019, 42:030601 doi: 10.11889/j.0253-3219.2019.hjs.42.030601Hu Jifeng, Wang Xiaohe, Li Wenjiang, et al. Uncertainties analysis of reactivity parameters caused by nuclear data of molten salt experiment reactor[J]. Nuclear Techniques, 2019, 42: 030601 doi: 10.11889/j.0253-3219.2019.hjs.42.030601 [14] 黄洪文, 武宇, 叶林, 等. 反应堆控制棒铪板性能研究[J]. 原子能科学技术, 2009, 43(s2):316-318Huang Hongwen, Wu Yu, Ye Lin, et al. Research of hafnium characteristic for control rod of reactor[J]. Atomic Energy Science and Technology, 2009, 43(s2): 316-318 [15] 阮锡超. 我国核数据实验研究进展[J]. 核技术, 2023, 46:080003 doi: 10.11889/j.0253-3219.2023.hjs.46.080003Ruan Xichao. Nuclear data measurement progress in China[J]. Nuclear Techniques, 2023, 46: 080003 doi: 10.11889/j.0253-3219.2023.hjs.46.080003 -
点击查看大图
图(6) / 表(3)
计量
- 文章访问数: 223
- HTML全文浏览量: 91
- PDF下载量: 23
- 被引次数: 0
