Predictive modeling of the surface pattern of double-sided polishing process of optical components
-
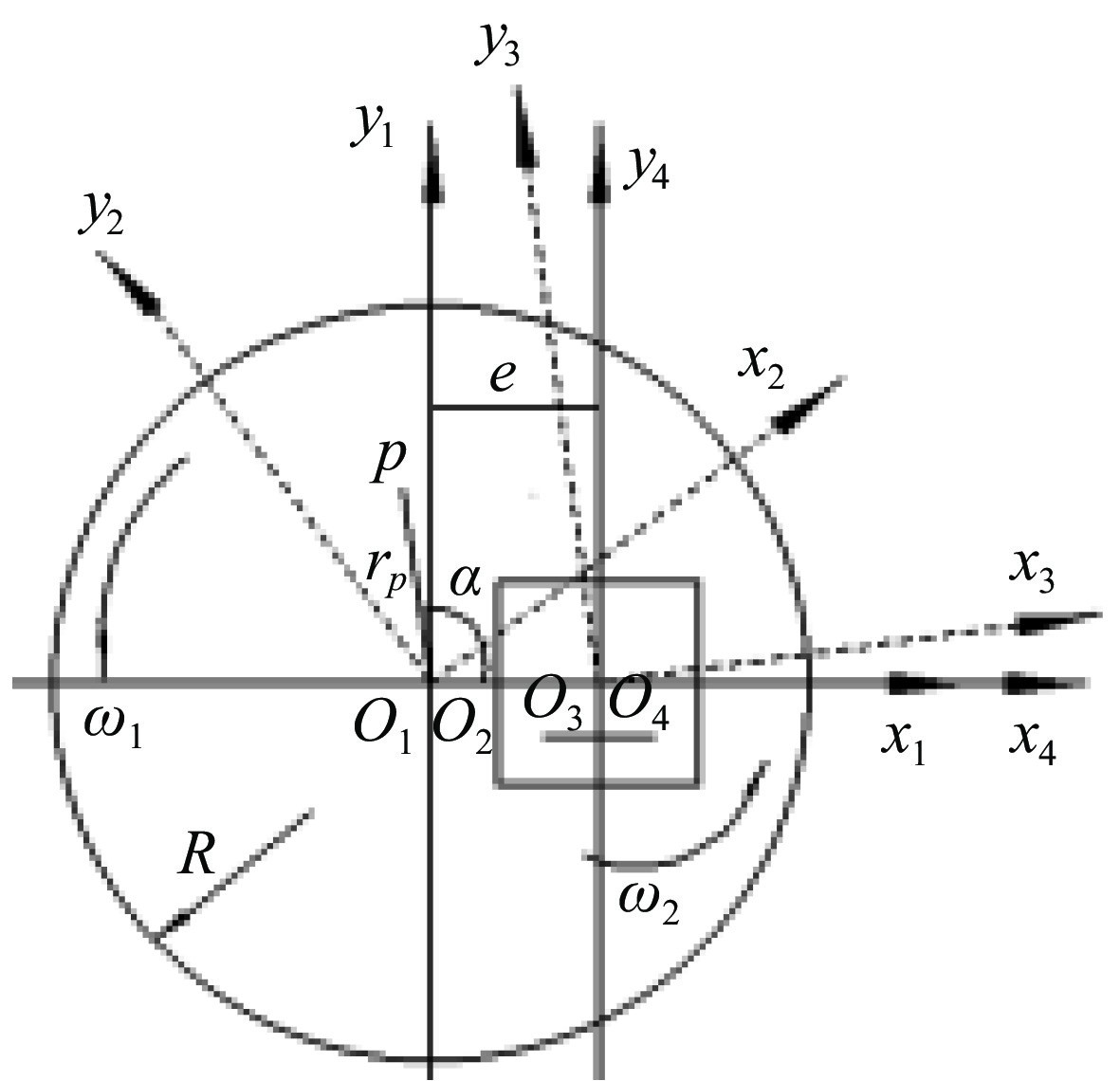
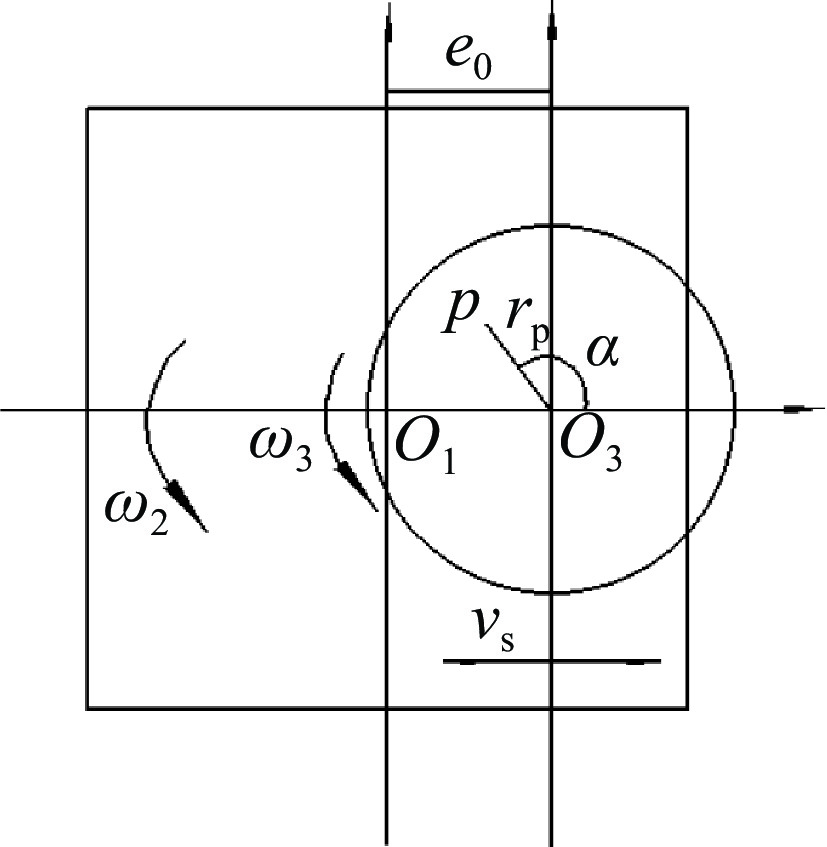
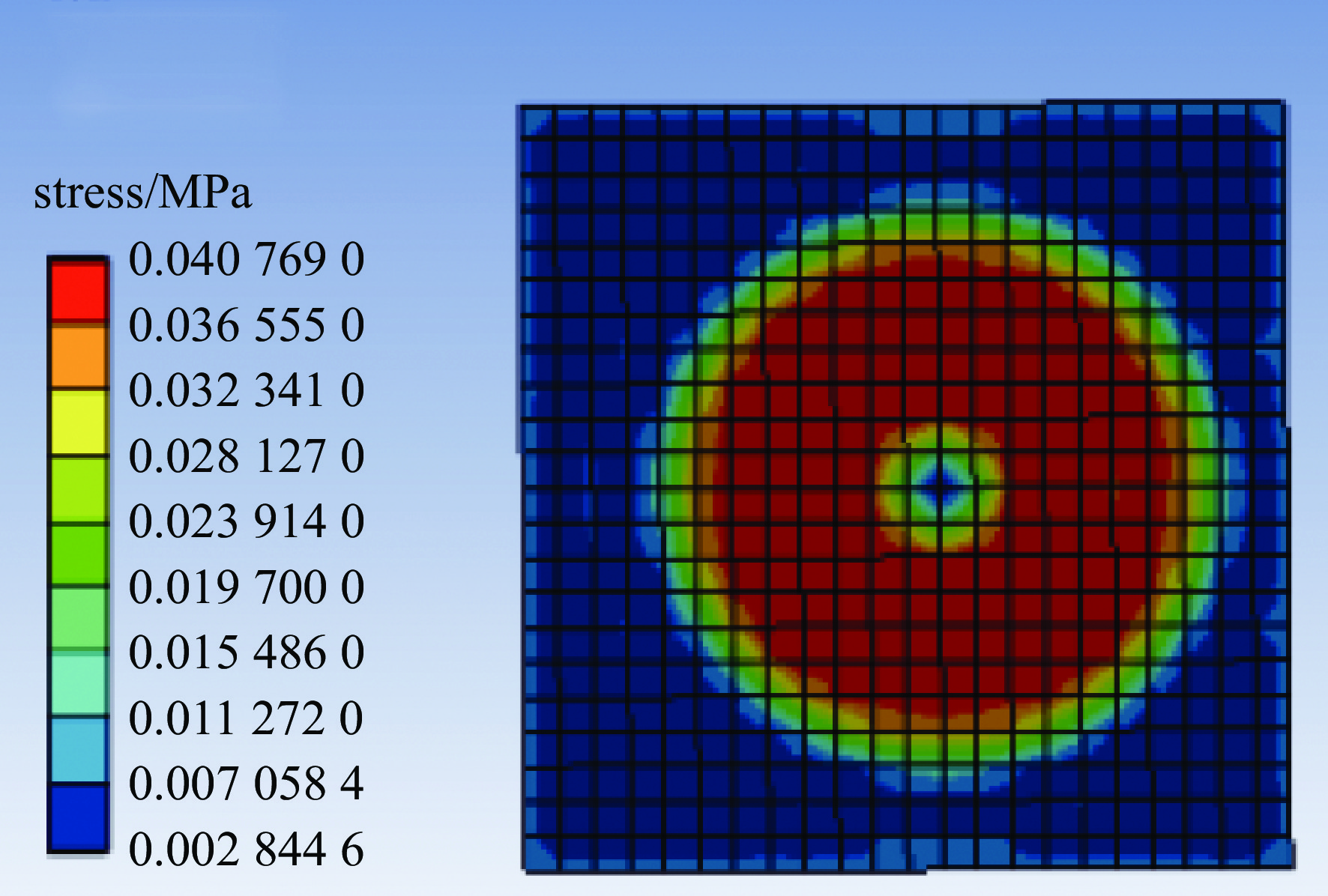
摘要: 针对双面抛光难以建立稳定去除函数进行加工面型预测这一问题,基于双面抛光加工原理,采用坐标变换法推导出元件上下表面相对速度分布方程,然后运用ANSYS软件仿真元件上下表面静态压力分布,采用多项式拟合法将仿真数据导入Matlab软件拟合出元件上下表面压力分布随时间变化公式。根据Preston方程推导修正系数K表达式,通过4组抛光实验数据计算出修正系数K值为2.588×10−15,构建双面抛光加工面型预测模型。最后通过加工实验验证该预测模型,实验结果表明预测PV值误差占元件实际加工后面型PV值的1.07%~7.4%,预测模型与实际加工后的面型吻合。Abstract: To address the challenge of establishing a stable removal function for double-sided polishing to predict the finished surface profile, we use the coordinate transformation method to derive the relative velocity distribution equations for the upper and lower surfaces of the component. Subsequently, static pressure distributions on both surfaces are simulated using ANSYS software. The simulation data is then imported into Matlab and fitted with a polynomial method to determine the time-varying pressure distribution formulas for the component's surfaces. Based on the Preston equation, an expression for the correction coefficient K is derived. The value of the correction coefficient K is calculated to be 2.588×10−15 from four sets of polishing experimental data, enabling the construction of a predictive model for the surface pattern in double-sided polishing processes. The predictive model is ultimately validated through machining experiments. The experimental results indicate that the error in predicting the PV (Peak-to-Valley) value accounts for 1.07% to 7.4% of the actual PV value after processing, demonstrating good agreement between the predicted model and the actual post-processing surface pattern.
-
Key words:
- double-sided polishing /
- surface pattern /
- predictive modeling /
- experimental validation
-
表 1 压力分布方程的系数
Table 1. Coefficients of pressure distribution equation
p00 p10 p01 p20 p11 p02 p30 p21 0.1528 − 0.002813 − 0.002813 2.042×10−5 5.041×10−5 2.044×10−5 −6.455×10−8 −1.173×10−7 p12 p03 p40 p31 p22 p13 p04 −1.172×10−7 −6.47×10−8 7.503×10−11 3.041×10−14 2.727×10−10 −1.021×10−13 7.528×10−11 表 2 修正实验中的抛光工艺参数
Table 2. Polishing process parameters in the modified experiment
experimental group
numberelement, upper plate,
lower plate/(r·mm−1)oscillation speed/
(mm·s−1)time/s swing distance/
mmdistance from the center of the element
to the center of the lower plate/mm1 10.1,10.9,10 5/6 2700 10 1260 2 12.1,12.9,10 5/6 1800 3 12.1,12.9,10 1/3 300 4 10.1,10.9,10 1/3 420 表 3 预测验证实验工艺参数及实验数据与预测数据对比
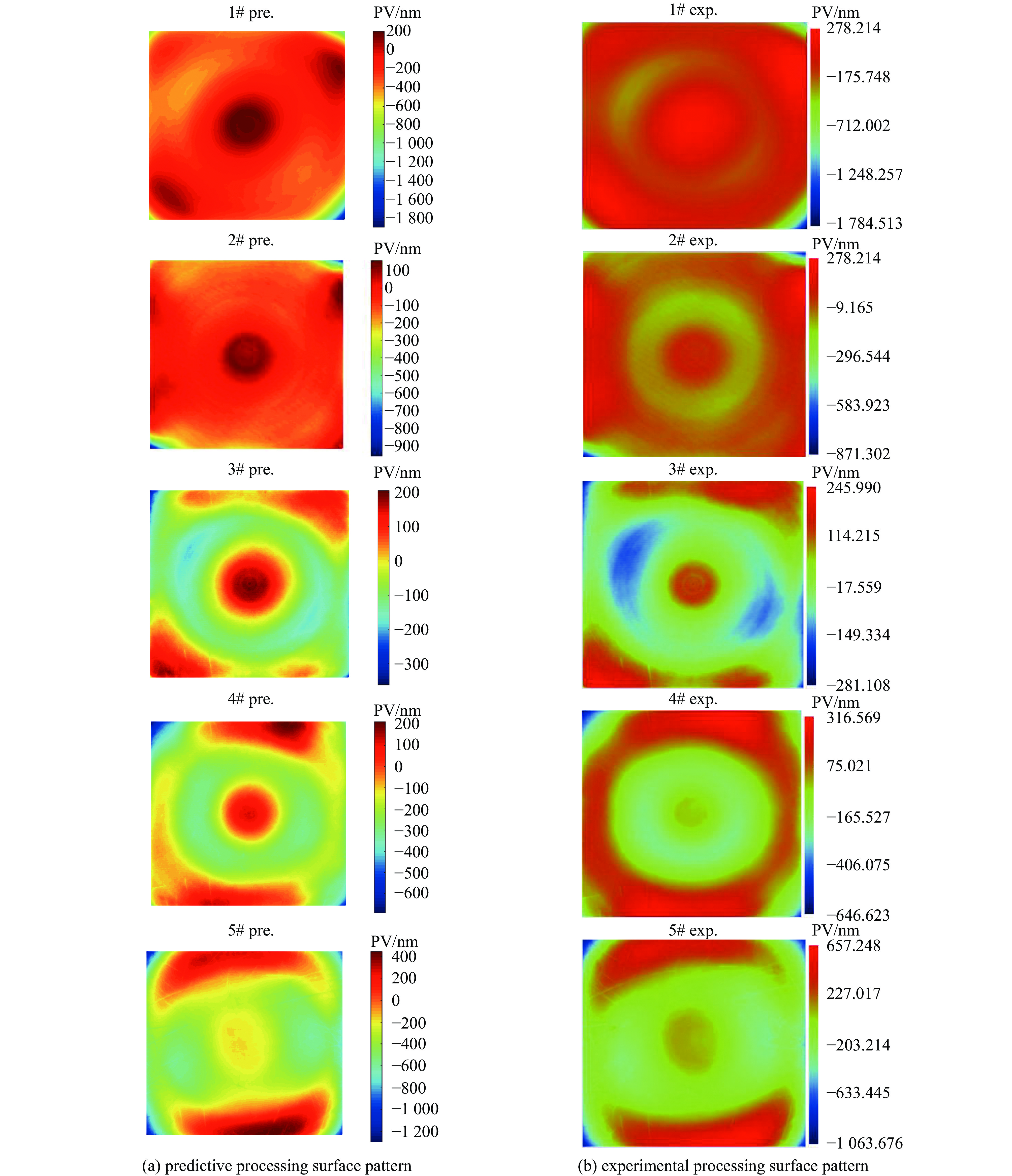
Table 3. Prediction-validated expermental process parameters and comparsion between experimental data predicted data
experimental
group
numberelement, upper
plate, lower
plate/(r·mm−1)oscillation
speed/
(mm·s−1)time/s swing
distance/
mmdistance from the center of
the element to the center of
the lower plate/mmexperimental PV
values/μmpredicted PV
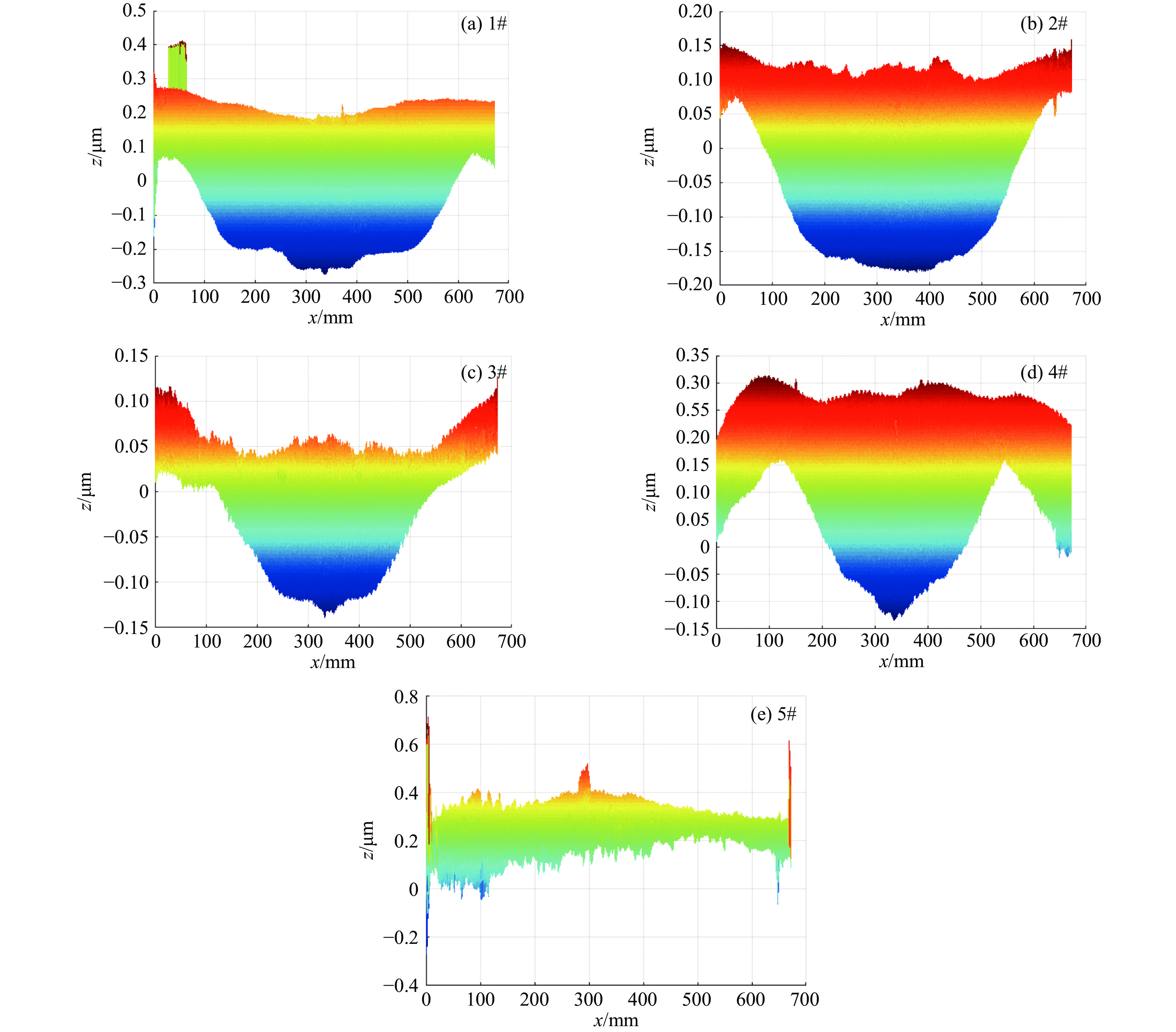
values/μm1# 12.1, 12.9, 10 5/6 2700 80 0, 1160 2.145 2.122 2# 12.1, 12.9, 10 2 900 10 0, 1160 1.149 1.122 3# 10.1, 10.9, 8 1/3 600 10 0, 1260 0.527 0.566 4# 10.1, 10.9, 10 1/3 1800 10 0, 1260 0.962 0.947 5# 10.1, 10.9, 10 2 3600 10 110, 1160 1.720 1.746 -
[1] Campbell J H, Hawley-Fedder R A, Stolz C J, et al. NIF optical materials and fabrication technologies: an overview[C]//Proceedings of SPIE 5341, Optical Engineering at the Lawrence Livermore National Laboratory II: The National Ignition Facility. 2004: 84-101. [2] Satake U, Enomoto T, Fujii K, et al. Optimization method for double-sided polishing process based on kinematical analysis[J]. Procedia CIRP, 2016, 41: 870-874. doi: 10.1016/j.procir.2015.12.043 [3] Hashimoto Y, Ozaki R, Furumoto T, et al. A calculation method for workpiece profile variation during double-sided lapping by considering workpiece elastic deformation[J]. Precision Engineering, 2022, 73: 457-469. doi: 10.1016/j.precisioneng.2021.09.016 [4] 王春阳, 帅闻, 肖博, 等. 基于环摆式双面抛光法加工预测模型的去除均匀性研究[J]. 光学学报, 2023, 43:0914001 doi: 10.3788/AOS221863Wang Chunyang, Shuai Wen, Xiao Bo, et al. Uniformity removal based on processing prediction model of ring-pendulum double-sided polishing method[J]. Acta Optica Sinica, 2023, 43: 0914001 doi: 10.3788/AOS221863 [5] 李振兴, 柏伟, 王琰璋, 等. 大尺寸非规则碲锌镉晶片双面抛光技术[J]. 人工晶体学报, 2023, 52(2):244-251Li Zhenxing, Bai Wei, Wang Yanzhang, et al. Study on double sided polishing technology of large size irregular CdZnTe wafer[J]. Journal of Synthetic Crystals, 2023, 52(2): 244-251 [6] 陈庚豪. 3英寸AT切石英晶圆抛光片内非均匀性研究[D]. 武汉: 华中科技大学, 2022CHEN Genghao. Research on non-uniformity of polishing 3-inch AT-cut quartz crystal wafer[D]. Wuhan: Huazhong University of Science and Technology, 2022 [7] 林涛. 基于磨粒磨损机制的光学元件快速抛光关键技术研究[D]. 厦门: 厦门大学, 2017Li Tao. Research on the optical element fast polishing key technology based on the abrasive wear mechanism[D]. Xiamen: Xiamen University, 2017 [8] 徐雳, 刘冰, 吴石, 等. 双面研磨/抛光机磨削轨迹研究[J]. 哈尔滨理工大学学报, 2018, 23(4):43-50Xu Li, Liu Bing, Wu Shi, et al. Double-sided lapping/polishing machine grinding trajectory studies[J]. Journal of Harbin University of Science and Technology, 2018, 23(4): 43-50 [9] 郭磊, 明子航, 靳淇超, 等. 弹性基体磨具的磨抛轨迹与表面加工质量研究[J]. 表面技术, 2022, 51(12):255-268Guo Lei, Ming Zihang, Jin Qichao, et al. Polishing trajectory and surface machining quality of elastic matrix abrasive tool[J]. Surface Technology, 2022, 51(12): 255-268 [10] 陈真, 杨炜, 郭隐彪. 快速抛光技术接触压力建模与仿真[J]. 厦门大学学报(自然科学版), 2012, 51(2):215-218Chen Zhen, Yang Wei, Guo Yinbiao. Modeling and simulation for contact pressure of fast polishing process[J]. Journal of Xiamen University (Natural Science), 2012, 51(2): 215-218 [11] 卢跃. 基于磨粒运动轨迹的端面磨削热力耦合过程分析[D]. 沈阳: 东北大学, 2019Lu Yue. Analysis of thermal mechanical coupling process of face grinding based on the movement trajectory of abrasive grains[D]. Shenyang: Northeastern University, 2019 [12] 王鹏里, 董志国, 轧刚, 等. 基于软性磨料流的Preston方程kp参数的修正与测定[J]. 科学技术与工程, 2018, 18(2):232-236Wang Pengli, Dong Zhiguo, Ya Gang, et al. Modification and determination of the Preston equation kp parameter based on soft abrasive flow[J]. Science Technology and Engineering, 2018, 18(2): 232-236 [13] Hashimoto Y, Furumoto T, Sato T, et al. Novel method to visualize Preston’s coefficient distribution for chemical mechanical polishing process[J]. Japanese Journal of Applied Physics, 2022, 61: 116502. doi: 10.35848/1347-4065/ac916b [14] 樊成. 光学曲面确定性抛光的面型精度控制研究[D]. 长春: 吉林大学, 2014Fan Cheng. Investigation on control of surface form accuracy for deterministic polishing of optical part surfaces[D]. Changchun: Jilin University, 2014 [15] Wang Lijuan, Hu Zhongwei, Fang Congfu, et al. Study on the double-sided grinding of sapphire substrates with the trajectory method[J]. Precision Engineering, 2018, 51: 308-318. doi: 10.1016/j.precisioneng.2017.09.001 [16] Bai Yifan, Xiao Bo, Wang Chunyang, et al. Polishing uniformity analysis and process optimization based on the kinematic model of ring pendulum double-sided polisher[J]. The International Journal of Advanced Manufacturing Technology, 2023, 126(11/12): 5689-5701. -




 下载:
下载: