电磁场B样条间断有限元方法

华沁怡; 李林; 齐红新

doi:10.11884/HPLPB202436.240076

电磁场B样条间断有限元方法

doi: 10.11884/HPLPB202436.240076

华沁怡^1,,
李林¹,
齐红新^2, ,

1.
华东师范大学精密光谱科学与技术国家重点实验室，上海 200241
2.
华东师范大学物理与电子科学学院，上海 200241

基金项目: 国家重点研发计划（2020YFA0709800）；国家自然科学基金项目（12192251、12274134）；上海市教委基金项目（2023ZKZD35）

详细信息

作者简介:
华沁怡，1098600977@qq.com

通讯作者:
齐红新，hxqi@phy.ecnu.edu.cn。

中图分类号: O441.4
计量
- 文章访问数: 199
- HTML全文浏览量: 121
- PDF下载量: 41
- 被引次数: 0
出版历程
- 收稿日期: 2024-03-06
- 修回日期: 2024-04-07
- 录用日期: 2024-04-07
- 网络出版日期: 2024-04-19
- 刊出日期: 2024-05-31

B-spline discontinuous Galerkin method for Maxwell’s equations

Hua Qinyi^1
,,
Li Lin¹,
Qi Hongxin^{2
, ,}

1.
State Key Laboratory of Precision Spectroscopy , East China Normal University, Shanghai 200241, China
2.
School of Physics and Electronic Science, East China Normal University, Shanghai 200241, China

摘要

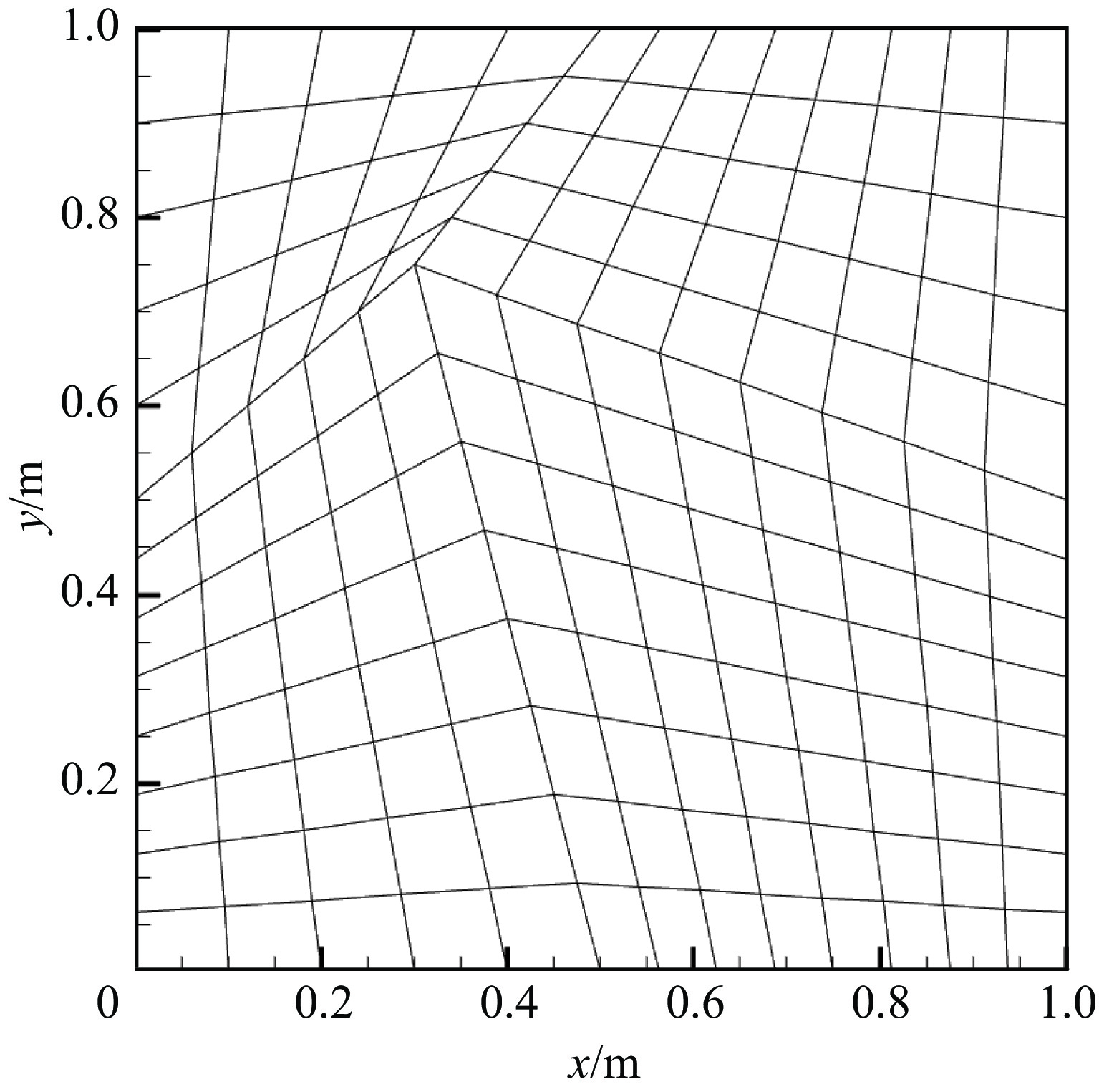
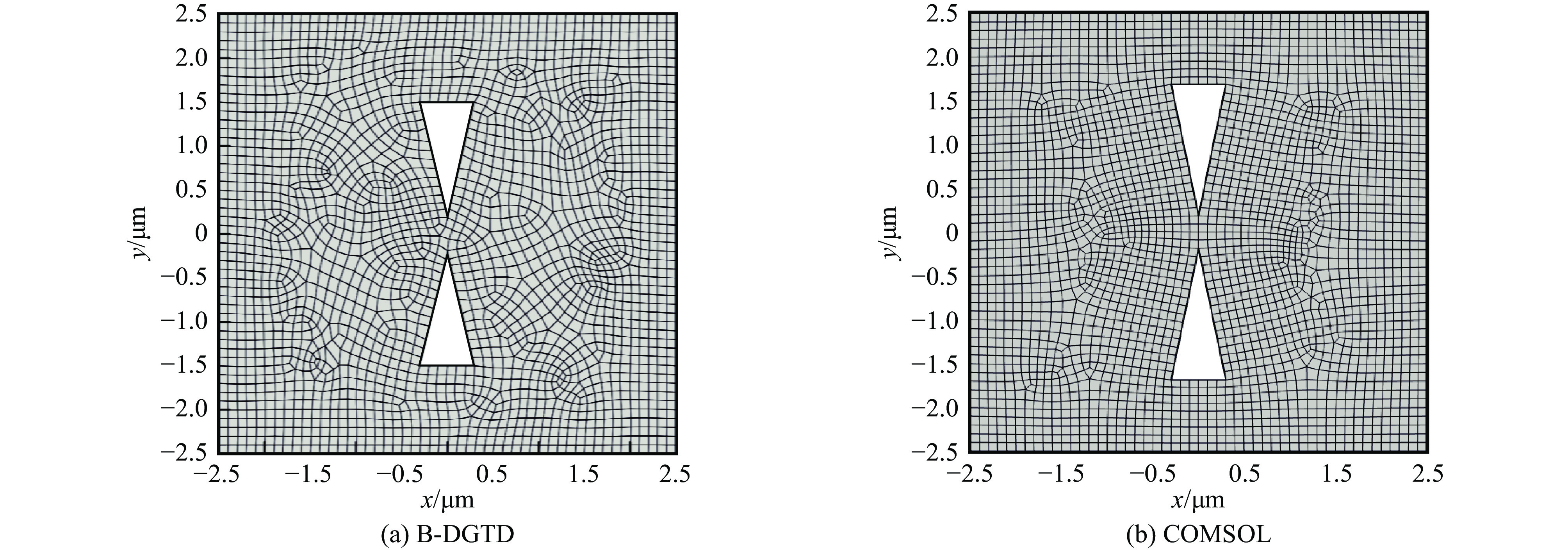
摘要: 在计算电磁学领域，时域间断有限元算法（DGTD）一般基于模型空间的不规则网格划分和单元上高阶多项式插值计算。同样的插值阶数，二维空间四边形网格划分比三角形网格划分具有更少的自由度和更高的计算效率。然而，传统基于等参变换和多项式张量积插值的基函数空间在四边形单元上仅具有低阶完备性，且稳定性和精度受网格畸变影响较大。为此，提出了一种基于不规则四边形网格的高阶B样条插值DGTD方法，用于Maxwell方程的求解。文章采用的B样条基不仅具有高阶多项式空间的插值完备性，而且完全消除了单元内部自由度。此外，Maxwell方程离散系统的各系数矩阵还具有精确的解析形式。使用该方法分析腔体的本征模和楔形体的电磁散射，结果表明，相较于COMSOL软件最大允许时间步长提高2.5倍，计算所需未知量减少25%，证实了本文算法的高稳定性和高精度特点。
- B样条 /
- 间断有限元 /
- 瞬态电磁学 /
- 高阶精度 /
- 畸变网格
Abstract: In the field of computational electromagnetics, the discontinuous Galerkin time domain (DGTD) method typically relies on irregular grid partitioning in model space and high-order polynomial interpolation calculations on elements. When comparing two-dimensional spatial quadrilateral mesh partitioning to triangular mesh partitioning at the same interpolation order, quadrilateral meshing offers fewer degrees of freedom and higher computational efficiency. However, traditional basis function spaces, relying on isoparametric transformations and polynomial tensor product interpolation, only possess low-order completeness on quadrilateral elements. Consequently, their stability and accuracy are significantly influenced by grid distortion. To address this challenge, this thesis proposes a high-order B-spline interpolation DGTD method based on irregular quadrilateral meshes for solving Maxwell's equations. The advantage of B-spline interpolation lies in its high-order completeness on irregular elements, effectively eliminating internal degrees of freedom within the elements. Furthermore, the coefficient matrices of the discrete system for Maxwell's equations also possess exact analytical forms. Analyzing the eigenmodes of cavities and the electromagnetic scattering of wedge structures, thus the maximum allowable time step increasing by 2.5 times and reducing the required unknowns by 25% compared to COMSOL software, the proposed algorithm exhibits notable advantages in terms of higher stability and precision.
- B-spline /
- discontinuous finite element /
- transient electromagnetics /
- high-order accuracy /
- distorted grid

HTML全文

图 1 凸四边形单元三次样条域点及插值节点分布

Figure 1. Distribution of points and interpolation nodes in cubic spline field of convex quadrilateral element

下载: 全尺寸图片幻灯片

图 2 方形谐振腔四边形网格划分

Figure 2. Quadrilateral meshing of square resonator

下载: 全尺寸图片幻灯片

图 3 不同模式下的本征谱

Figure 3. Eigen frequency of different modes

下载: 全尺寸图片幻灯片

图 4 模式(3,1)相对误差随网格精度的变化

Figure 4. Variation of relative error with mesh size

下载: 全尺寸图片幻灯片

图 5 (4,1)模式下$ {E}_{y} $相对误差随网格尺寸的变化

Figure 5. Relative error of (4,1) mode with mesh size

下载: 全尺寸图片幻灯片

图 6 六种共振模式下$ {E}_{y} $分布

Figure 6. Square vacuum cavity: component $ {E}_{y} $ of six resonant modes

下载: 全尺寸图片幻灯片

图 7 测量点处数值结果与参考值的误差比较

Figure 7. Error comparison of numerical results with reference values at measuring point

下载: 全尺寸图片幻灯片

图 8 不同监视点数值结果和参考结果的波形对比

Figure 8. Comparison of numerical results and reference results of different monitor points

下载: 全尺寸图片幻灯片

图 9 电磁波传播至右侧总场边界时的场分布

Figure 9. Distribution of electromagnetic wave propagating to the right boundary of total field

下载: 全尺寸图片幻灯片

图 10 不同网格划分对比

Figure 10. Comparison of mesh distribution

下载: 全尺寸图片幻灯片

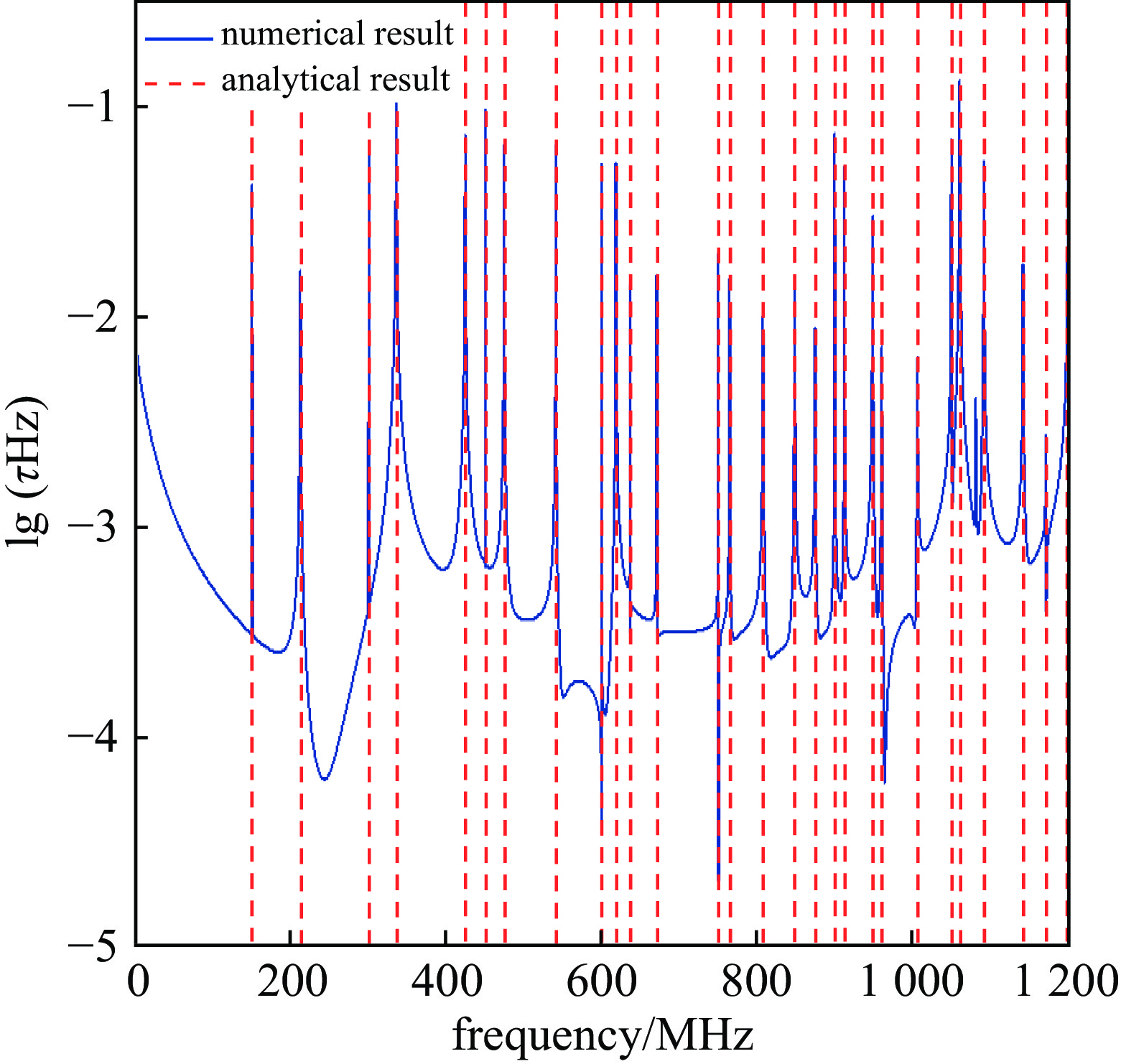
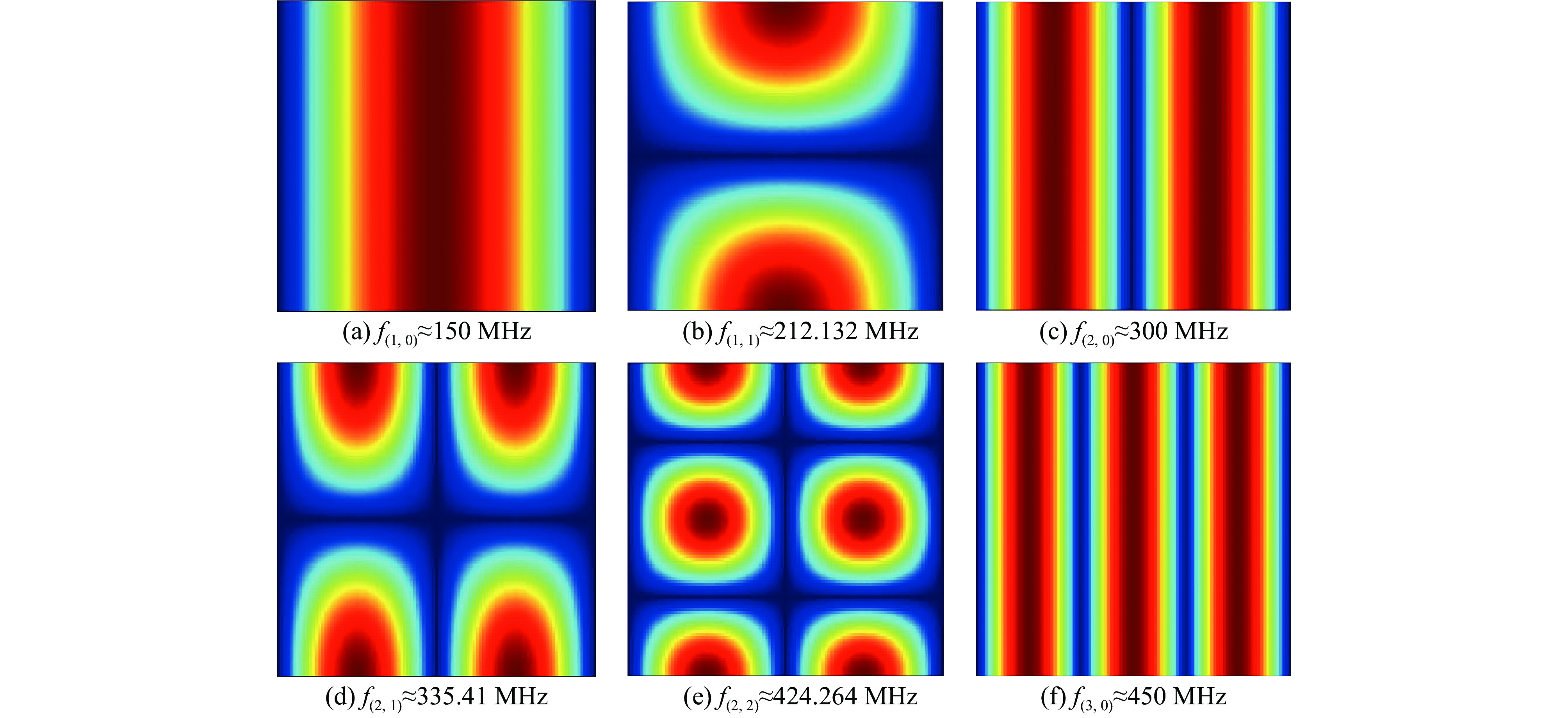
表 1 腔体的谐振频率

Table 1. Analytical and numerical results for resonant frequencies of different modes

mode	analytical/MHz	B-DGTD/MHz	error (B-DGTD)/%	COMSOL/MHz	error (COMSOL)/%
(1,0)	150.000	150.002	0.0013	149.540	0.3067
(3,2)	540.833	540.800	0.0061	541.598	0.1414
(4,1)	618.466	618.400	0.0107	622.269	0.6149
(4,4)	848.528	848.399	0.0152	847.794	0.0865
(5,3)	874.643	874.480	0.0186	878.505	0.4416
(6,2)	948.528	948.800	0.0287	950.451	0.2027
(7,1)	1060.660	1060.974	0.0296	1062.114	0.1371
(10,0)	1500.000	1500.481	0.0321	1501.771	0.1181
(11,0)	1650.000	1650.589	0.0357	1645.462	0.2750
(11,1)	1656.804	1657.584	0.0471	1665.451	0.5219

下载: 导出CSV

参考文献(16)

[1]	Joseph R M, Taflove A. FDTD Maxwell's equations models for nonlinear electrodynamics and optics[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(3): 364-374. doi: 10.1109/8.558652
[2]	Goorjian P M, Taflove A, Joseph R M, et al. Computational modeling of femtosecond optical solitons from Maxwell's equations[J]. IEEE Journal of Quantum Electronics, 1992, 28(10): 2416-2422. doi: 10.1109/3.159548
[3]	Körpinar T, Demirkol R C, Körpinar Z, et al. Maxwellian evolution equations along the uniform optical fiber[J]. Optik, 2020, 217: 164561. doi: 10.1016/j.ijleo.2020.164561
[4]	Anttu N, Mäntynen H, Sorokina A, et al. Applied electromagnetic optics simulations for nanophotonics[J]. Journal of Applied Physics, 2021, 129(13): 131102. doi: 10.1063/5.0041275
[5]	Zhelyeznyakov M V, Brunton S L, Majumdar A. Deep learning to accelerate Maxwell’s equations for inverse design of dielectric metasurfaces[C]//2021 Conference on Lasers and Electro-Optics (CLEO). 2021: 1-2.
[6]	Zhao Ying, Lan Jun, Ding Dazhi. A high-order time-domain discontinuous Galerkin integral equation method for analysis of multiscale PEC objects[J]. IEEE Antennas and Wireless Propagation Letters, 2024, 23(1): 104-108. doi: 10.1109/LAWP.2023.3318249
[7]	Dong Ming, Chen Liang, Li Ping, et al. Discontinuous Galerkin time-domain method in electromagnetics: from nanostructure simulations to multiphysics implementations[M]//Ren Qiang, Yan Su, Elsherbeni A Z. Advances in Time-Domain Computational Electromagnetic Methods. Hoboken: Wiley, 2022: 135-198.
[8]	Ainsworth M. Dispersive and dissipative behaviour of high order discontinuous Galerkin finite element methods[J]. Journal of Computational Physics, 2004, 198(1): 106-130. doi: 10.1016/j.jcp.2004.01.004
[9]	van Willenswaard L J C, Smeets S, Renaud N, et al. Computation of optical properties of real photonic band gap crystals as opposed to utopian ones[C]//2023 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference. 2023: ck_p_38.
[10]	Yee K S, Chen J S. The finite-difference time-domain (FDTD) and the finite-volume time-domain (FVTD) methods in solving Maxwell's equations[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(3): 354-363. doi: 10.1109/8.558651
[11]	Collino F, Fouquet T, Joly P. Conservative space-time mesh refinement methods for the FDTD solution of Maxwell’s equations[J]. Journal of Computational Physics, 2006, 211(1): 9-35. doi: 10.1016/j.jcp.2005.03.035
[12]	Inan U S, Marshall R A. Numerical electromagnetics: the FDTD method[M]. Cambridge: Cambridge University Press, 2011.
[13]	Gedney S D. Introduction to the finite-difference time-domain (FDTD) method for electromagnetics[M]. Cham: Springer Nature, 2011.
[14]	Busch K, König M, Niegemann J. Discontinuous Galerkin methods in nanophotonics[J]. Laser & Photonics Reviews, 2011, 5(6): 773-809.
[15]	Kennedy C A, Carpenter M H, Lewis R M. Low-storage, explicit Runge–Kutta schemes for the compressible Navier–Stokes equations[J]. Applied Numerical Mathematics, 2000, 35(3): 177-219. doi: 10.1016/S0168-9274(99)00141-5
[16]	陈娟. 基于多元样条插值的有限元方法[M]. 北京: 科学出版社, 2020 Chen Juan. Finite element method based on multivariate spline interpolation[M]. Beijing: Science Press, 2020