基于神经网络反向模型的系统级电场辐射发射预测

刘璐瑶; 金晓; 蔡金良

doi:10.11884/HPLPB202436.240177

基于神经网络反向模型的系统级电场辐射发射预测

doi: 10.11884/HPLPB202436.240177

刘璐瑶^{1, 2, 3,},
金晓^{1, 4},
蔡金良^{1, 4}

1.
中国工程物理研究院应用电子学研究所，四川绵阳 621999
2.
中国电子科技集团公司第二十九研究所，成都 610036
3.
中国工程物理研究院研究生院，北京 100088
4.
先进激光与高功率微波全国重点实验室，四川绵阳 621900

详细信息

作者简介:
刘璐瑶，shakiibaby@163.com

中图分类号: TM743
计量
- 文章访问数: 180
- HTML全文浏览量: 72
- PDF下载量: 44
- 被引次数: 0
出版历程
- 收稿日期: 2024-05-24
- 修回日期: 2024-07-22
- 录用日期: 2024-07-22
- 网络出版日期: 2024-07-25
- 刊出日期: 2024-08-16

Prediction of system-level electric field radiated emission based on ANN reverse model

Liu Luyao^{1, 2, 3
,},
Jin Xiao^{1, 4},
Cai Jinliang^{1, 4}

1.
Institute of Applied Electronics, CAEP, Mianyang 621999, China
2.
The 29th Research Institute of China Electronics Technology Group Corporation, Chengdu 610036, China
3.
Graduate School of China Academy of Engineering Physics, Beijing 100088, China
4.
National Key Laboratory of Science and Technology on Advanced Laser and High Power Microwave, Mianyang 621900, China

摘要

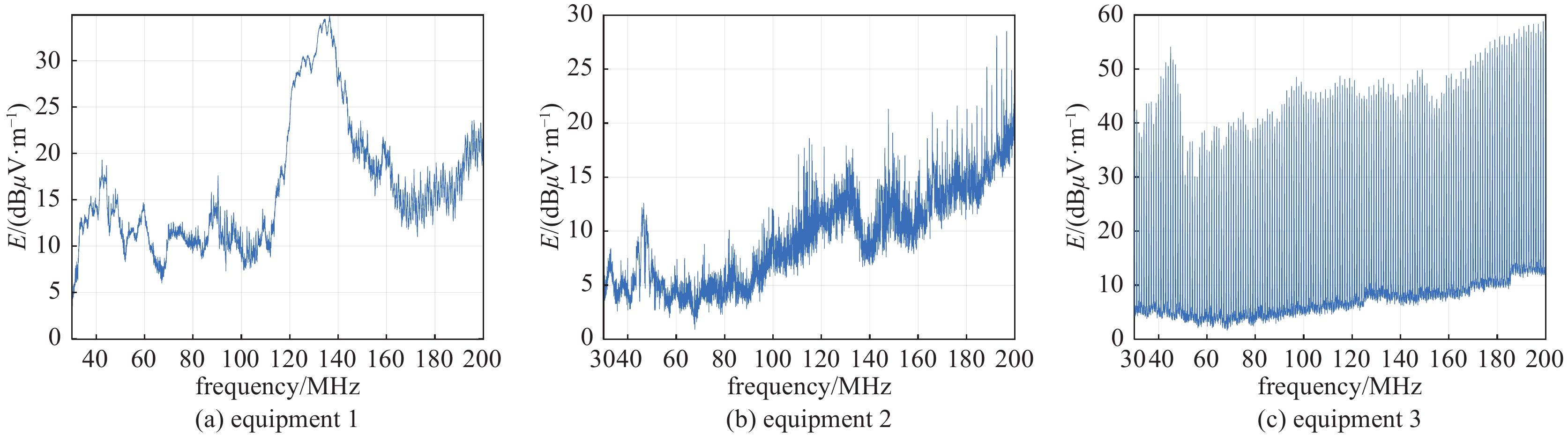
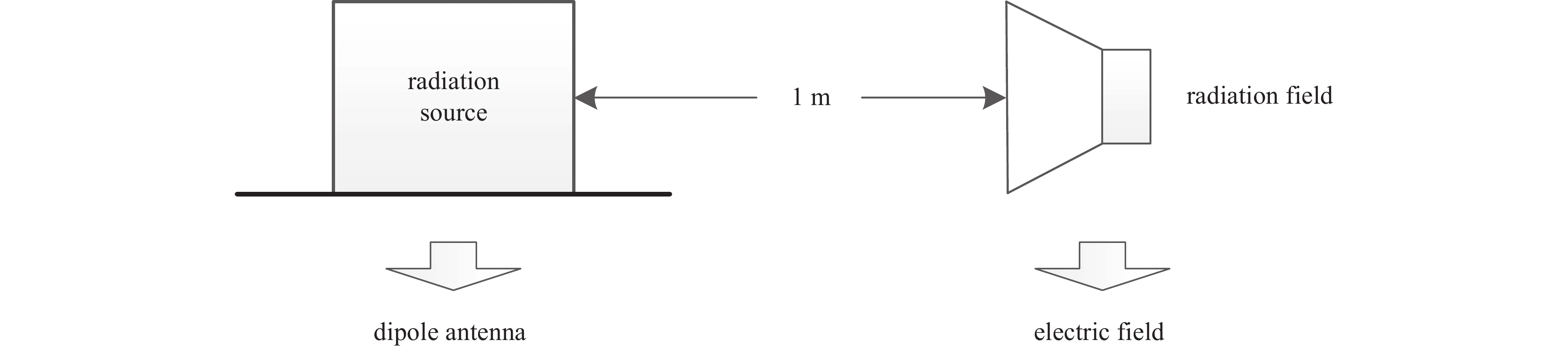
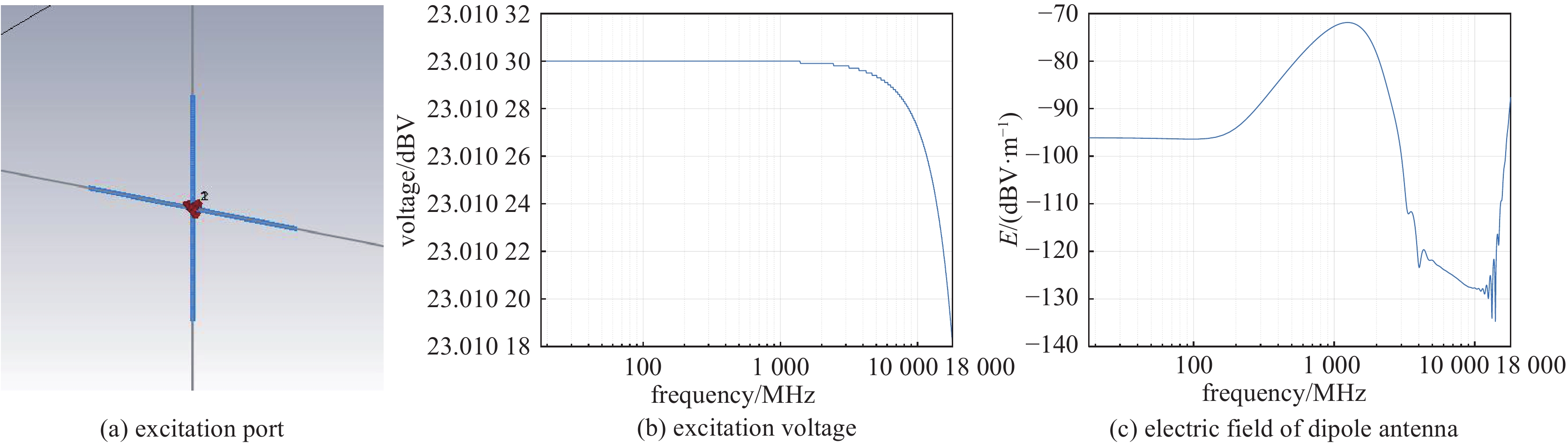
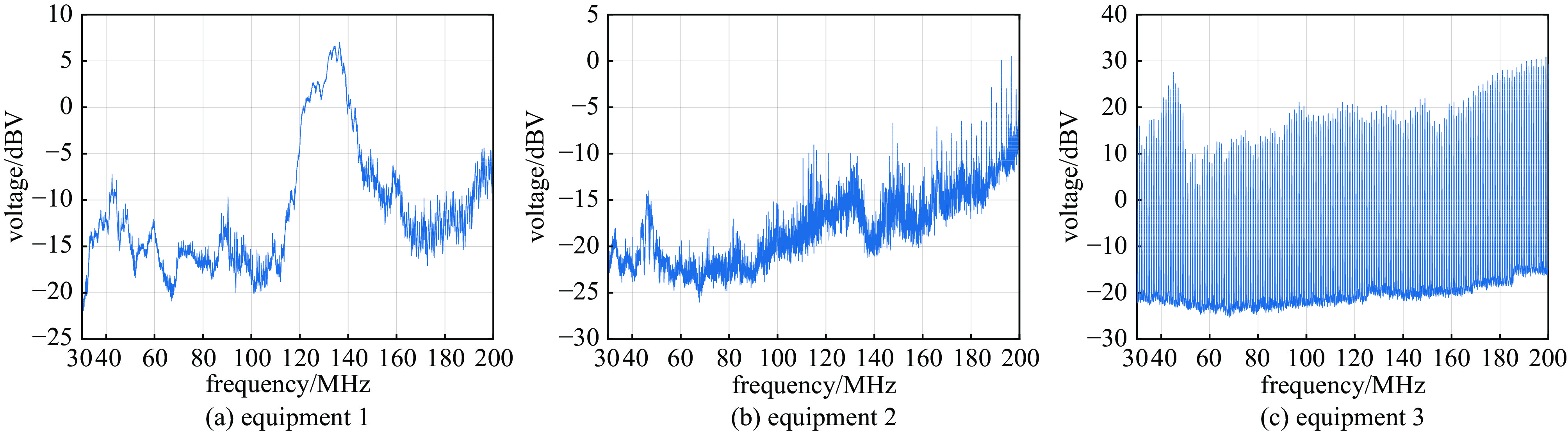
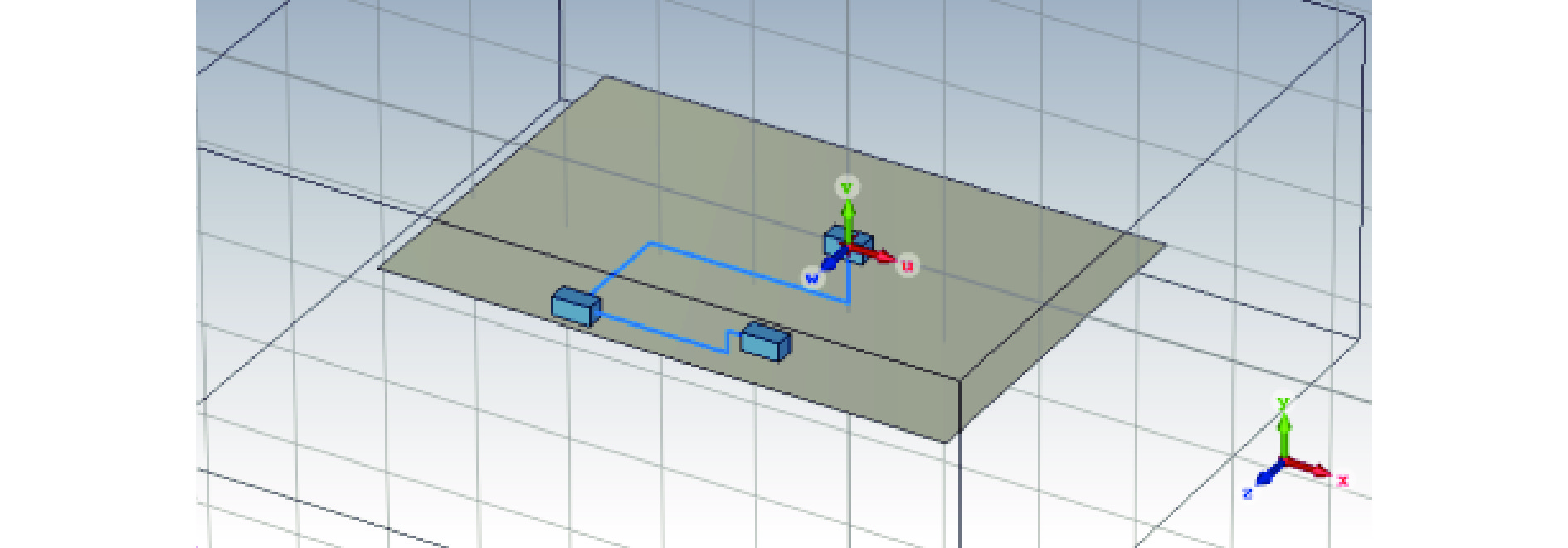
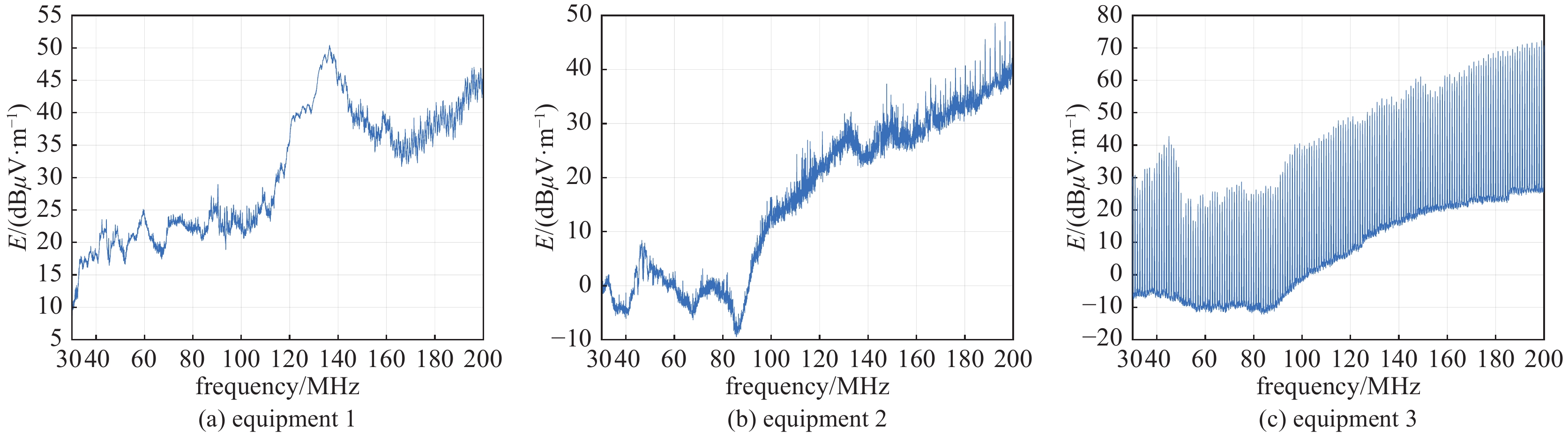
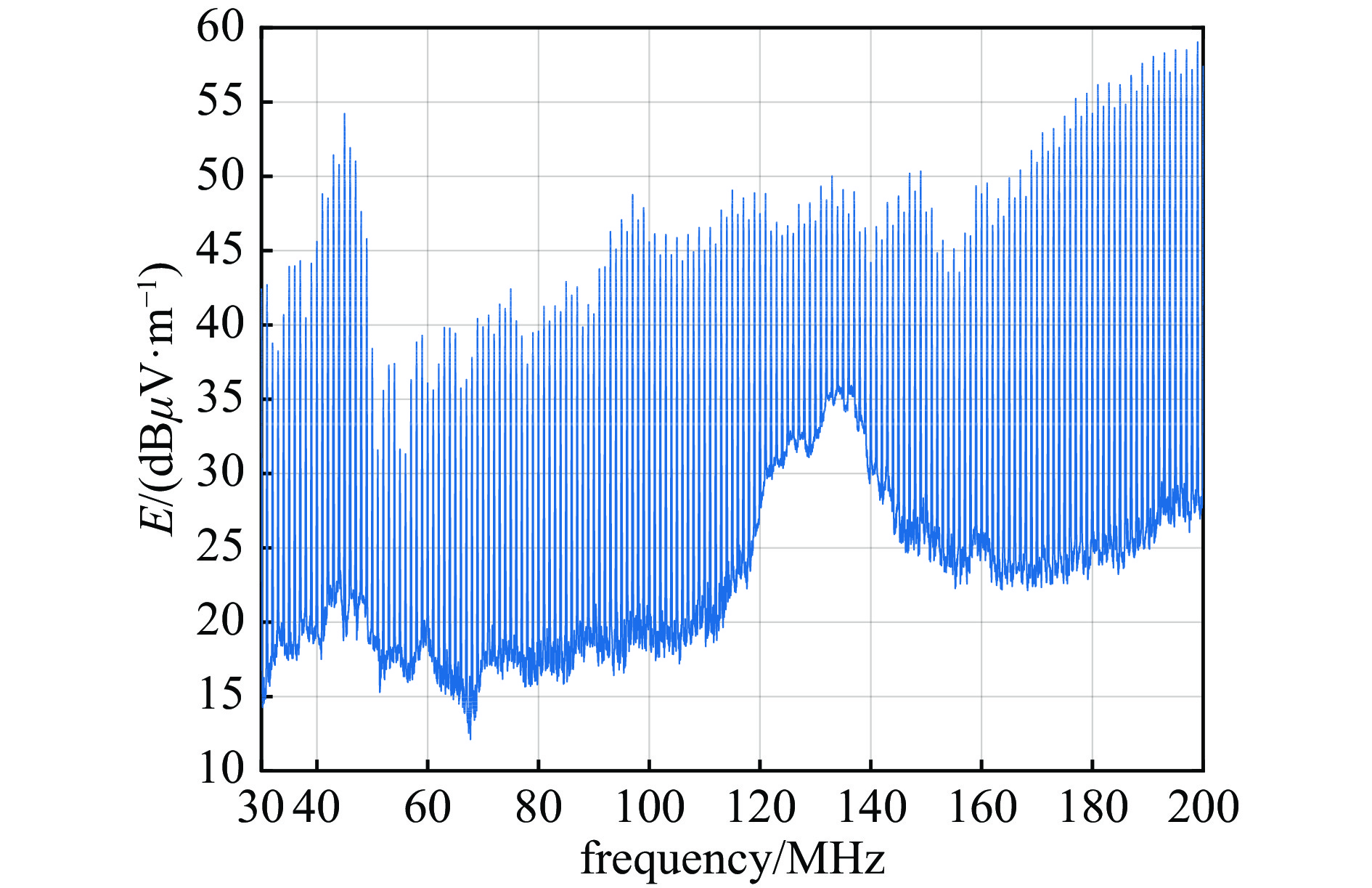
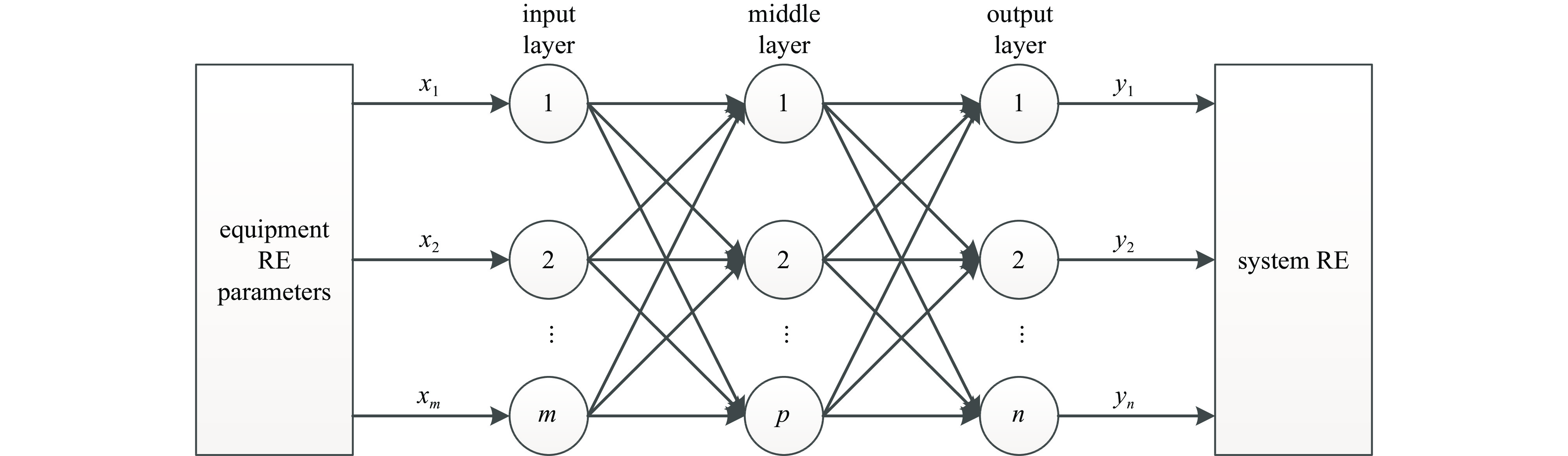
摘要: 针对多设备叠加系统级电磁兼容性问题，提出了一种基于神经网络反向模型的复杂系统电磁干扰预测新方法。首先实测单设备电场辐射发射数据，通过噪声源辐射发射等效性原理仿真多设备叠加的系统级电场辐射发射，获取训练样本集。选择各设备辐射场强、频率、坐标为输入参数，以系统级电场辐射发射为输出参数，建立基于Levenberg-Marquardt （LM）算法的三层逆向传播（BP）神经网络的反向模型，将神经网络的输入、输出反向，寻找验证误差最小的备选神经网络作为最终的神经网络，并结合试位法和共轭梯度法等数值求解算法计算神经网络输出。结果表明，该模型仿真的验证误差较传统三层LM-BP神经网络改善明显，其中采用共轭梯度法求解的神经网络反向模型将验证误差由0.4159%减小到了0.0997%。该方法不仅不依赖于复杂的神经网络结构，且在有限的训练数据规模下提高了模型精度，为舰船、卫星、飞机等电子信息平台的电磁兼容性评估提供了一种新的高效解决途径。
- 神经网络 /
- 电磁兼容 /
- 辐射发射 /
- 数值求解方法 /
- 非线性系统
Abstract: To address the issue of system-level electromagnetic compatibility, a new method of predicting electromagnetic interference of complex systems based on artificial neural network (ANN) reverse model is proposed in this paper. Firstly, the electric field radiated emission (RE) of single equipment is measured. The training data of system-level RE are obtained by simulation based on the equivalence principle of radiated emission. Frequency, RE and coordinate of each single equipment are selected as the input variables, and the system-level RE is the output variable. A reverse model of the three-layer back-propagation (BP) ANN with Levenberg-Marquardt (LM) algorithm is established by exchanging the input–output variables. The alternative ANN with minimum validation error is searched as the ultimate ANN. The numerical root-finding algorithm (regular-falsi method and conjugate gradient method) are adopted to calculate the RE of multi equipments. The results show that the validation error of this reverse model is significantly improved compared to the traditional three-layer LM-BP ANN. Especially, the ANN reverse model based on conjugate gradient method reduces the validation error from 0.4159% to 0.0997%. This method is independent of complex ANN structures, and improves simulation accuracy with limited training data, which provides a new efficient and feasible solution for electromagnetic compatibility evaluation of electronic information platforms such as ships, satellites, and aircrafts.
- artificial neural network /
- electromagnetic compatibility /
- radiated emission /
- root-finding algorithm /
- nonlinear system

HTML全文

图 1 RE102测试布置

Figure 1. RE102 test setup

下载: 全尺寸图片幻灯片

图 2 单设备RE102测试数据

Figure 2. RE102 test data of single equipment

下载: 全尺寸图片幻灯片

图 3 辐射发射等效性原理

Figure 3. Equivalence principle of radiated emission (RE)

下载: 全尺寸图片幻灯片

图 4 等效偶极子天线模型与仿真

Figure 4. Model and simulation of dipole antenna

下载: 全尺寸图片幻灯片

图 5 各设备的等效辐射源

Figure 5. Equivalent radiation source of each equipment

下载: 全尺寸图片幻灯片

图 6 仿真模型

Figure 6. Simulation model

下载: 全尺寸图片幻灯片

图 7 各设备单独开机下系统电场辐射发射

Figure 7. System RE while single equipment operating

下载: 全尺寸图片幻灯片

图 8 所有设备同时开机状态下系统电场辐射发射

Figure 8. System RE while all equipments operating

下载: 全尺寸图片幻灯片

图 9 三层LM-BP神经网络模型

Figure 9. Three level LM-BP ANN

下载: 全尺寸图片幻灯片

表 1 验证数据集

Table 1. Validation dataset

No.	f/MHz	x₁	y₁	z₁	E₁/(dBuV/m)	x₂	y₂	z₂	E₂/(dBuV/m)	x₃	y₃	z₃	E₃/(dBuV/m)	E_total/(dBuV/m)
1	30	0	0	−100	4.3	1000	120	−100	4.3	1050	310	−750	42.2	31.939571
2	70	0	0	−100	10.9	1000	120	−100	3.2	1050	310	−750	39.4	40.123183
3	100	0	0	−100	9.2	1000	120	−100	10.7	1050	310	−750	45.2	53.036382
4	130	0	0	−100	30.5	1000	120	−100	11.5	1050	310	−750	45.3	60.507379
5	160	0	0	−100	19.9	1000	120	−100	11.6	1050	310	−750	48.3	64.899009
6	200	0	0	−100	20.9	1000	120	−100	17.3	1050	310	−750	57.2	77.367965
7	30	0	100	−200	4.3	900	200	−200	4.3	1000	400	−600	42.2	35.062737
8	70	0	100	−200	10.9	900	200	−200	3.2	1000	400	−600	39.4	43.601726
9	100	0	100	−200	9.2	900	200	−200	10.7	1000	400	−600	45.2	56.07834
10	130	0	100	−200	30.5	900	200	−200	11.5	1000	400	−600	45.3	62.877408
…	…	…	…	…	…	…	…	…	…	…	…	…	…	…
25	30	−200	0	−400	4.3	1200	150	−150	4.3	1200	200	−800	42.2	32.92811
26	70	−200	0	−400	10.9	1200	150	−150	3.2	1200	200	−800	39.4	40.90428
27	100	−200	0	−400	9.2	1200	150	−150	10.7	1200	200	−800	45.2	54.0078
28	130	−200	0	−400	30.5	1200	150	−150	11.5	1200	200	−800	45.3	61.66204
29	160	−200	0	−400	19.9	1200	150	−150	11.6	1200	200	−800	48.3	65.79797
30	200	−200	0	−400	20.9	1200	150	−150	17.3	1200	200	−800	57.2	77.72475

下载: 导出CSV

表 2 不同训练样本数量下的模型验证误差及相关性系数

Table 2. Validation error and relative coefficient of different number of training dataset

number of training dataset	validation error/%	relative coefficient
30	7.7008	0.85303
100	0.8713	0.87193
200	0.4159	0.95546
500	0.0059	0.99809
1000	3.4247E-5	0.99977
10000	2.2718E-5	0.99991

下载: 导出CSV

表 3 备选神经网络

Table 3. Alternative neural network

No.	alternative neural network	validation error/%
1	x_1,c=f_ann,1(y, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃)	0.149589782
2	x_2,c=f_ann,2(x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃)	0.000017400
3	x_3,c=f_ann,3(x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃)	0.096499053
4	x_4,c=f_ann,4(x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃)	0.003367234
5	x_5,c=f_ann,5(x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃)	3.945121882
6	x_6,c=f_ann,6(x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃)	0.000000768
7	x_7,c=f_ann,7(x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃)	0.20383497
8	x_8,c=f_ann,8(x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃)	0.000812276
9	x_9,c=f_ann,9(x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃)	26.19090216
10	x_10,c=f_ann,10(x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃)	8.284504188
11	x_11,c=f_ann,11(x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃)	0.061618247
12	x_12,c=f_ann,12(x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃)	0.430195851
13	x_13,c=f_ann,13(x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃)	10.20954216

下载: 导出CSV

表 4 预测结果对比

Table 4. Comparison of prediction results

No.	E_total/(dBμV·m⁻¹)
No.	CST simulation	traditional LM-BP ANN	ANN reverse model (conjugate gradient method)	ANN reverse model (regular-falsi method)
1	31.94	45.64	30.34	31.04
2	40.12	52.91	38.11	39.00
3	53.04	56.41	52.91	51.55
4	60.51	48.03	60.33	58.81
5	64.90	58.98	65.98	63.08
6	77.37	60.86	76.63	75.20
7	35.06	54.04	26.02	34.08
8	43.60	55.38	36.43	42.38
9	56.08	60.12	49.31	54.51
10	62.88	56.28	65.89	61.11
11	67.58	60.84	66.36	65.68
12	80.09	63.85	74.17	77.84
13	33.37	60.00	33.68	32.44
14	40.88	62.78	41.72	39.73
15	53.74	60.13	53.21	52.23
16	60.87	61.54	60.15	59.17
17	65.84	65.62	66.13	63.99
18	78.86	68.21	78.36	76.65
19	32.80	47.91	27.05	31.88
20	41.02	53.70	37.33	39.87
21	53.80	55.91	48.49	52.29
22	61.09	52.69	59.88	59.38
23	65.67	59.85	60.61	63.83
24	78.14	64.56	65.75	75.95
25	32.93	58.02	31.77	32.00
26	40.90	57.64	38.76	39.76
27	54.01	56.90	53.70	52.49
28	61.66	60.12	60.52	59.93
29	65.80	61.43	67.04	63.95
30	77.72	66.63	77.63	75.55

下载: 导出CSV

参考文献(15)

[1]	赵辉. 系统电磁兼容[M]. 北京: 国防工业出版社, 2019 Zhao Hui. System electromagnetic compatibility[M]. Beijing: National Defense Industry Press, 2019
[2]	Kraft C H. Modeling leakage through finite apertures with TLM[C]//Proceedings of the IEEE Symposium on Electromagnetic Compatibility. 1994: 73-76.
[3]	Kunz K S, Luebbers R J. The finite difference time domain method for electromagnetics[M]. Boca Raton: CRC Press, 1993.
[4]	Cerri G, De Leo R, Primiani V M. Theoretical and experimental evaluation of the electromagnetic radiation from apertures in shielded enclosure[J]. IEEE Transactions on Electromagnetic Compatibility, 1992, 34(4): 423-432. doi: 10.1109/15.179275
[5]	李永明, 祝言菊, 李旭, 等. 电磁兼容的人工神经网络预测技术分析[J]. 重庆大学学报, 2008, 31(11):1313-1316,1322 Li Yongming, Zhu Yanju, Li Xu, et al. Artificial neural networks-based prediction of electromagnetic compatibility problems[J]. Journal of Chongqing University, 2008, 31(11): 1313-1316,1322
[6]	Shi Dan, Gao Yougang. A new method for identifying electromagnetic radiation sources using backpropagation neural network[J]. IEEE Transactions on Electromagnetic Compatibility, 2013, 55(5): 842-848. doi: 10.1109/TEMC.2012.2237176
[7]	Shi Dan, Fang Wei, Zhang Fangfei, et al. A novel method for intelligent EMC management using a “knowledge base”[J]. IEEE Transactions on Electromagnetic Compatibility, 2018, 60(6): 1621-1626. doi: 10.1109/TEMC.2018.2797053
[8]	Kuo M J, Lin T C. Dynamical optimal training for behavioral modeling of nonlinear circuit elements based on radial basis function neural network[C]//Proceedings of 2008 Asia-Pacific Symposium on Electromagnetic Compatibility and 19th International Zurich Symposium on Electromagnetic Compatibility. 2008.
[9]	Li Xu, Yu Jihui, Zhu Yanju, et al. Prediction of electromagnetic compatibility problems based on artificial neural networks[C]//Proceedings of 2008 World Automation Congress. 2008.
[10]	Belkacem F T, Bensetti M, Laour M, et al. The analytical, numerical and neural network evaluation versus experimental of electromagnetic shielding effectiveness of a rectangular enclosure with apertures[C]//Proceedings of the IEEE 9th International Conference on Cybernetic Intelligent Systems. 2010.
[11]	Devabhaktuni V, Bunting C F, Green D, et al. A new ANN-based modeling approach for rapid EMI/EMC analysis of PCB and shielding enclosures[J]. IEEE Transactions on Electromagnetic Compatibility, 2013, 55(2): 385-394. doi: 10.1109/TEMC.2012.2214223
[12]	Chahine I, Kadi M, Gaboriaud E, et al. Using neural networks for predicting the integrated circuits susceptibility to conducted electromagnetic disturbances[C]//Proceedings of 2007 18th International Zurich Symposium on Electromagnetic Compatibility. 2007: 13-16.
[13]	Burghardt F, Garbe R. Introduction of artificial neural networks in EMC[C]//Proceedings of 2018 IEEE Symposium on Electromagnetic Compatibility, Signal Integrity and Power Integrity. 2018.
[14]	Hager W W, Zhang Hongchao. A new conjugate gradient method with guaranteed descent and an efficient line search[J]. SIAM Journal on Optimization, 2005, 16(1): 170-192. doi: 10.1137/030601880
[15]	丛爽. 面向MATLAB工具箱的神经网络理论与应用[M]. 合肥: 中国科学技术大学出版社, 2009 Cong Shuang. Neural network theory and applications with MATLAB toolboxes[M]. Hefei: University of Science and Technology of China Press, 2009