Segment-smoothed Bayesian iterative method to reconstruct pulsed X-ray spectrum
-
摘要: 吸收法测量脉冲X射线能谱时,测量数据的微小扰动会引起重建能谱的较大波动,甚至出现不符合物理规律的负值。针对测量数据的噪声对脉冲X射线重建能谱影响较大的问题,构建了重建能谱准确性的评估方法,分析了贝叶斯迭代法对包含不同程度噪声干扰的测量数据重建能谱的准确性。通过在贝叶斯迭代法中加入平滑约束条件的方式,降低了噪声对重建能谱的影响。根据预估待测能谱的特征,提出了以能谱峰值为界分段平滑的方法,比较了整体平滑和分段平滑方法的能谱重建效果。多次求解表明,分段平滑贝叶斯迭代法的重建能谱对噪声的敏感度显著下降。设计了基于吸收法的能谱测量系统,分别利用平滑前后的贝叶斯迭代法依据实验测量数据重建能谱,结果表明,分段平滑的贝叶斯迭代法的重建能谱更接近理论能谱,重建效果更好。Abstract: Minor discrepancies in the measurement data may lead to significant variations in the reconstructed spectrum when measuring and reconstructing the spectrum by the absorption method. In some cases, the reconstructed spectrum may contain negative values that do not conform to the physical law. To address the issue that noise in the measurement data has a significant effect on the reconstructed spectrum, the segment-smoothed Bayesian iterative method is proposed in this paper. The energy spectrum is reconstructed using the Bayesian iteration method under different levels of noise, and the accuracy and noise sensitivity of the reconstructed spectrum are evaluated. An optimization method, which adds smoothing constraints to the Bayesian iterative method, is proposed to reduce noise interference in the reconstructed spectrum. According to the spectrum characteristics, a two-coefficient segment-smoothing method is proposed with the peak value as the dividing line. The spectrum is reconstructed by segmented smoothing and global smoothing Bayesian iterative methods, respectively. The noise sensitivity of the reconstructed spectrum, unfolded by the segment-smoothed Bayesian iterative method, has been significantly reduced. An energy spectrometer based on the absorption method is developed. The spectrum is reconstructed based on the experimental data using the segment-smoothed Bayesian iterative method and the Bayesian iteration method. The spectrum reconstructed using the segment-smoothed Bayesian iterative method is more consistent with the theoretical spectrum, indicating that this method exhibits superior performance.
-
能谱是反映脉冲X射线特性的一项重要指标。不同能量的光子与物品作用时发生的效应不同,准确获得脉冲X射线的能谱对于计算脉冲X射线的能注量、脉冲X射线在物体中的能量沉积[1]、医疗和工业CT成像[2-4]、获得原子核激发态能级[5]等具有重要意义。国内外对脉冲X射线能谱的测量方法有着广泛的研究,如康普顿散射法[6-7]、荧光法[8-10]、吸收法[4, 11-13]等,其中基于脉冲X射线衰减特性的吸收法是能谱测量的一种代表性方法[4, 11-13]。吸收法通过探测器阵列记录一组经过不同程度衰减后的脉冲X射线强度波形,结合脉冲X射线衰减系数和探测器的能量沉积构建关于测量数据和待求能谱的方程组,通过求解方程组重建脉冲X射线能谱。然而,当光子能量较高时,衰减系数随光子能量变化不明显,方程组呈现高度病态,测量值的微小扰动会引起重建能谱的较大波动,甚至在能谱中出现不符合物理规律的负值。并且在实验测量中,测量数据不可避免地会受到测量系统底噪、光子散射噪声、环境噪声等多种干扰的影响,在测量数据引入误差,影响能谱重建结果。
针对高度病态方程求解的问题,Iwasaki等人[14]将能谱重建与贝叶斯理论相结合,给出了基于贝叶斯原理的迭代求解方法,Yasushi Nauchi等人[15]证明了在不考虑测量误差情况下基于贝叶斯原理的迭代法的收敛性,该方法已被应用在伽马射线能谱和剂量的实时测量[16-18]、中子能谱的推导[19]、工业CT的X射线能谱测量及无损检测的图像重建[20-21]等领域中。但当测量数据中包含较高幅度的噪声时,贝叶斯迭代法重建能谱的准确性降低,能谱形状与预估理论能谱的误差较大。因此,降低贝叶斯迭代法对噪声的敏感度十分重要。
在此背景下,本文首先理论模拟了测量数据中包含不同幅度、不同类型的噪声时贝叶斯迭代法的能谱重建效果,分析了贝叶斯迭代法对噪声的敏感度。为降低重建能谱的随机性和对噪声的敏感度,在迭代过程中加入平滑约束条件,并针对预估脉冲X射线能谱的特征提出分段平滑的贝叶斯迭代法,减小噪声对重建能谱的影响。最后设计了基于吸收法的能谱测量系统,实验对比加入平滑约束前后的贝叶斯迭代法能谱重建效果。
1. 能谱测量及基于贝叶斯迭代法的能谱重建技术
1.1 吸收法用于脉冲X射线能谱测量
吸收法基于不同能量脉冲X射线衰减系数不同的特性测量能谱,依据预估待测能谱的能量范围,选取吸收片材料和厚度。在吸收片阵列后由探测器阵列记录衰减的脉冲X射线强度,结合不同能段脉冲X射线在探测器上的能量沉积矩阵,求解式(1)重建脉冲X射线能谱。
Ti=M∑j=1AijΦj (1) 式中:Ti是探测器的测量值,表示待测脉冲X射线经过第i个吸收片后,在第i个探测器上沉积的能量;Aij是第j个能段的光子经过第i个吸收片后在探测器上的理论沉积能量,由蒙特卡罗算法计算得到;Φj是第j个能段的相对光子数。
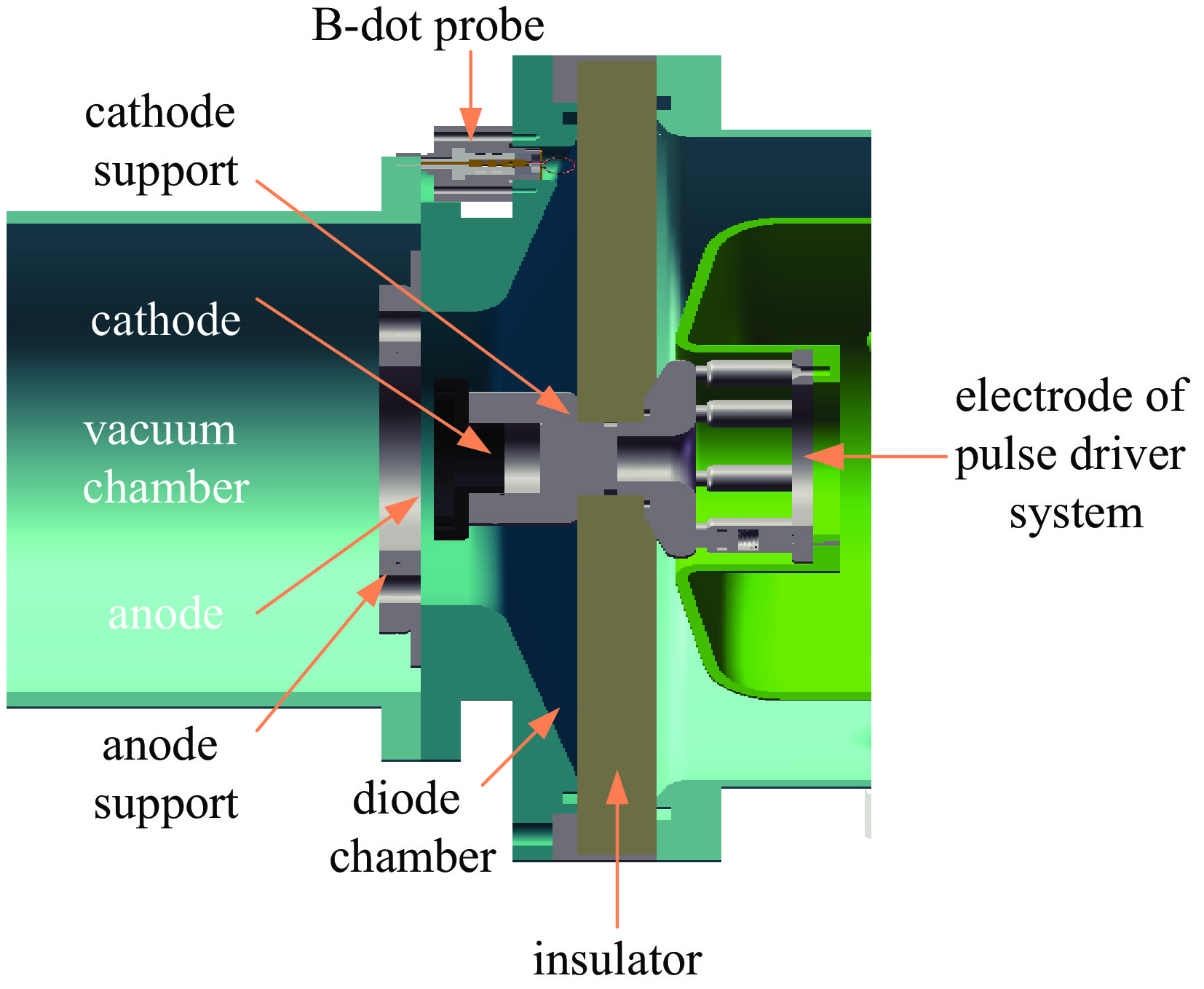
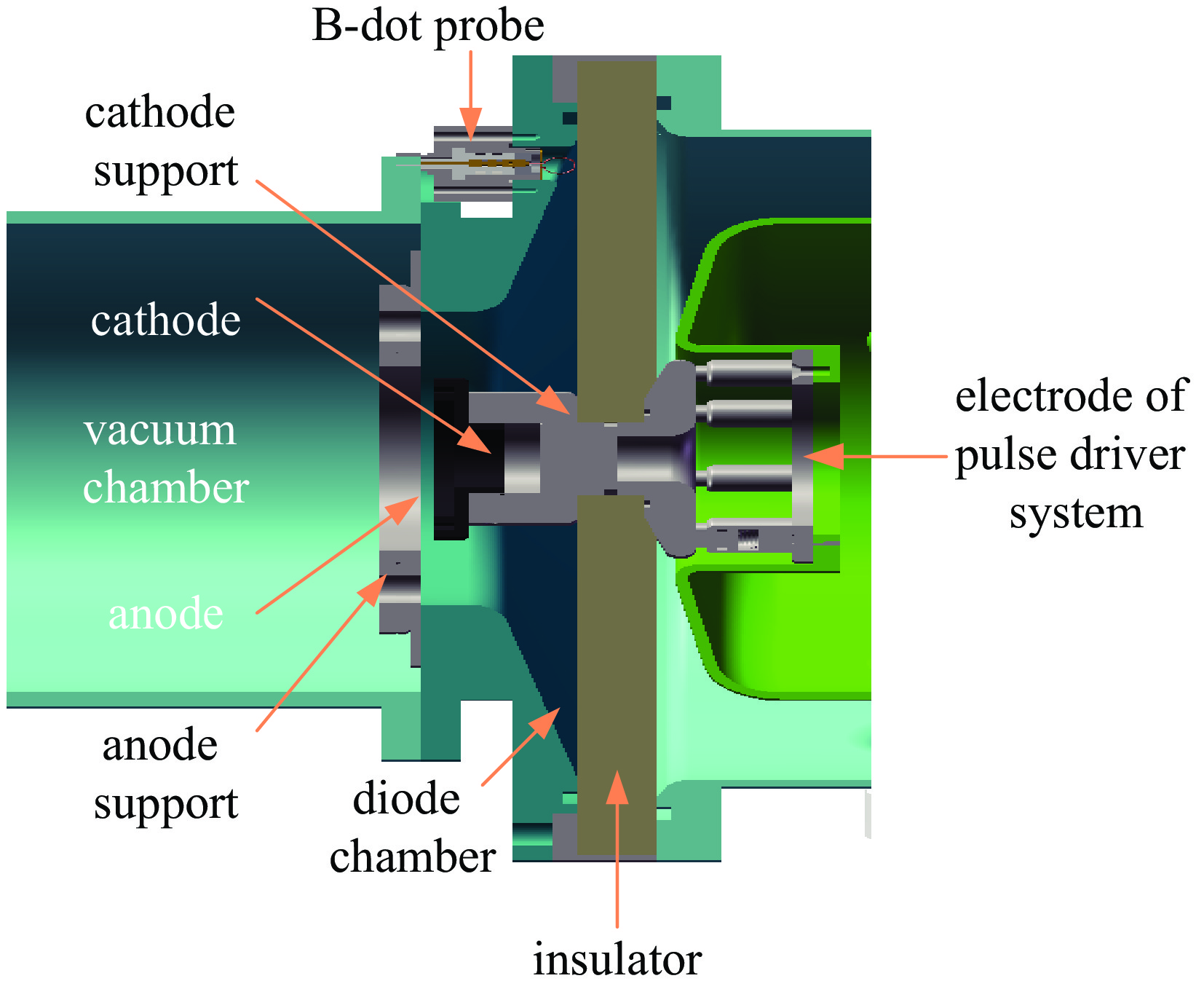
本文以电子束轰击20 μm钽靶产生的脉冲X射线为例研究能谱重建方法。以蒙特卡罗方法计算电子束轰击20 μm钽靶产生脉冲X射线的能谱作为理论能谱,其中电子束由峰值200 kV、脉冲半高宽30 ns的脉冲电压施加在等效阻抗2 Ω的二极管产生,二极管为径向绝缘结构,如图1所示。计算理论能谱和重建能谱时,均以5 keV为间隔划分能段。分析不同能谱重建方法的准确性时,将不考虑噪声时探测器的沉积能量称为探测器的理论沉积能量,根据吸收片厚度和探测器结构,由蒙特卡罗方法计算得到。根据实验噪声的数值模拟模型,分别对探测器的理论沉积能量叠加不同类型、不同水平的噪声扰动,将经噪声扰动后的数据称为含噪声的沉积能量。
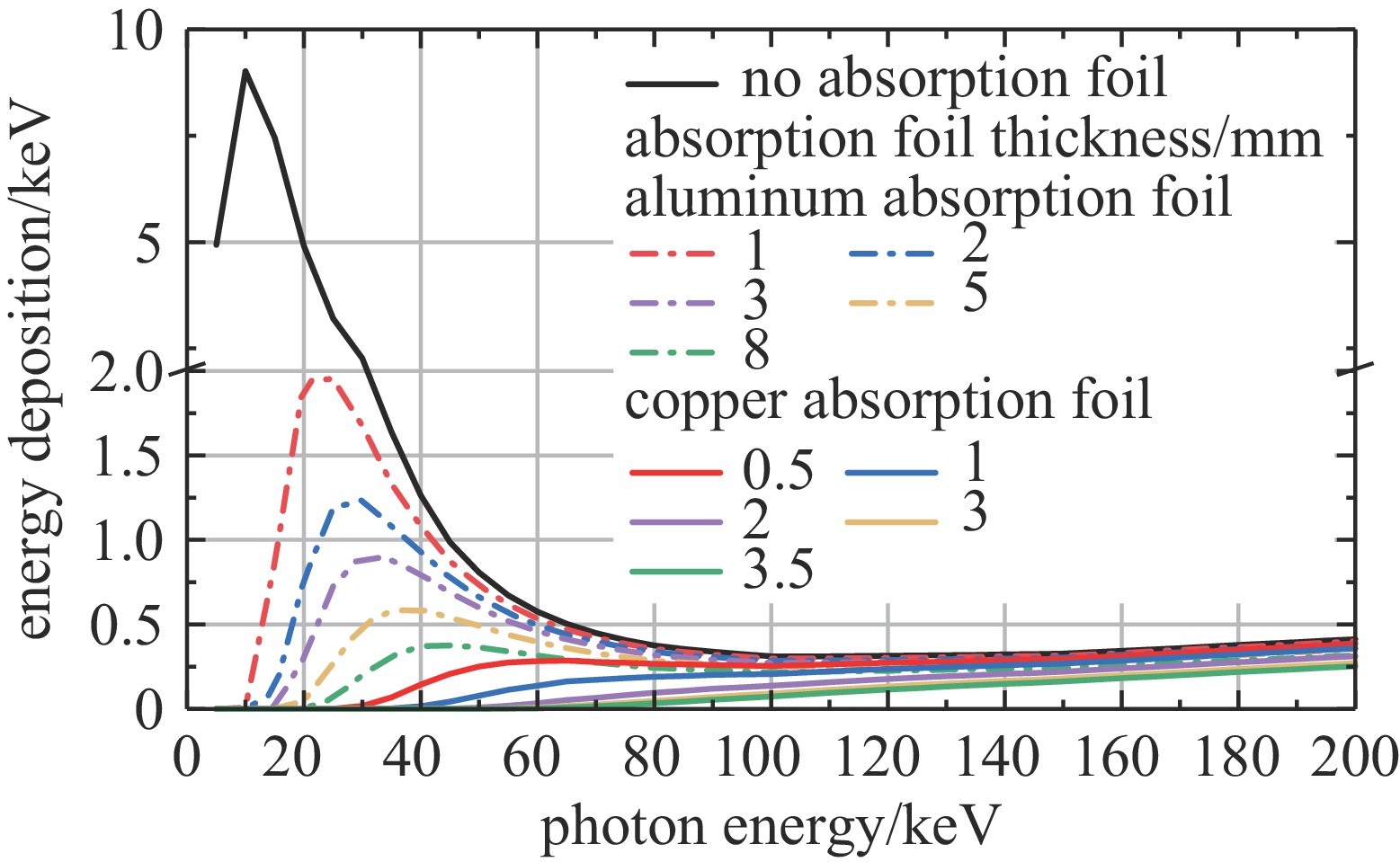
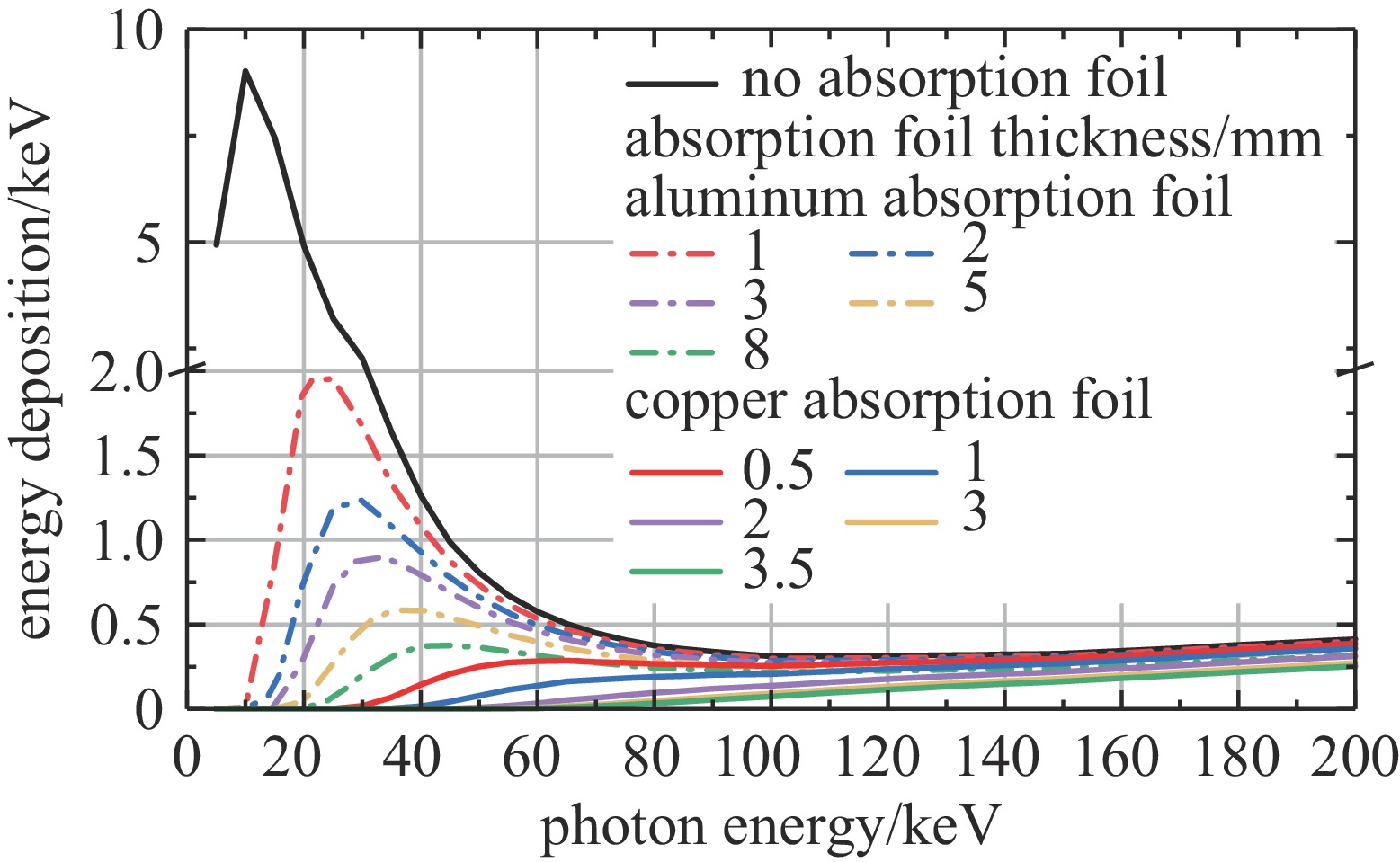
吸收片材料和厚度影响重建能谱的分辨能力。采取全电磁粒子模拟方法和蒙特卡罗方法联合计算,得到待测能谱经过不同厚度铝和铜吸收片后在探测器上的能量沉积,作为吸收片的选取依据。探测器选用Si-PIN探测器,灵敏区为硅材料,半径10 mm,厚300 μm。根据计算结果,选择厚1、2、3、5、8 mm的铝,厚0.5、1、2、3、3.5 mm的铜共10路吸收片和1路无吸收片。假设无吸收片时探测器上的能量沉积为E0,则11路测量通道对应的探测器上能量沉积分别为E0、0.47E0、0.36E0、0.29E0、0.21E0、0.14E0、0.10E0、0.053E0、0.024E0、0.014E0和0.011E0,构成了良好的衰减梯度。计算得到能量200 keV以内各能段的光子经吸收片衰减后在11路探测器上的沉积能量如图2所示。在能量大于90 keV的高能部分,吸收片材料和厚度的变化对探测器上沉积能量的影响微弱,方程呈高度病态,难以直接求解。
1.2 贝叶斯迭代法的能谱重建原理及结果
Iwasaki等人[14]提出将贝叶斯定理应用于能谱重建中,依据贝叶斯定理推导得到重建能谱的迭代公式
Φk+1j=1N∑i=1AijN∑i=1TiΦkj×AijM∑j=1Φkj×Aij (2) 式中:Φjk为第j个能段在第k次迭代后的光子数目。
求解时,给定任意全部为正的能谱初值,进行多次迭代,设定迭代终止条件,得到待求脉冲X射线能谱。贝叶斯迭代法为无偏估计方法,具有求解原理简单、能谱非负等特点[21]。设定第k次迭代后的能谱Φk与k+1次迭代后的能谱Φk+1的二范数‖Φk+1−Φk‖2小于特定值作为迭代终止条件,得到重建能谱。
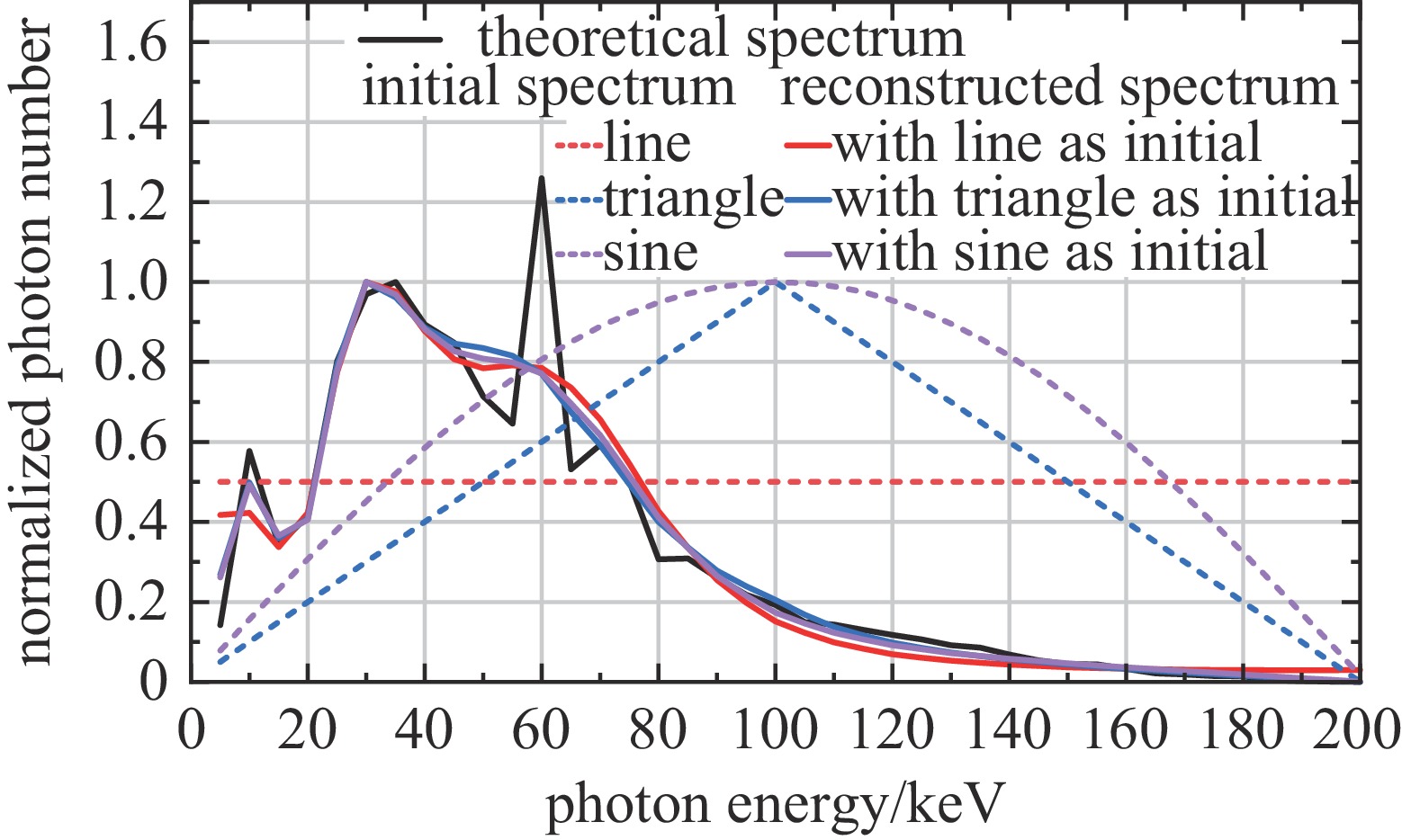
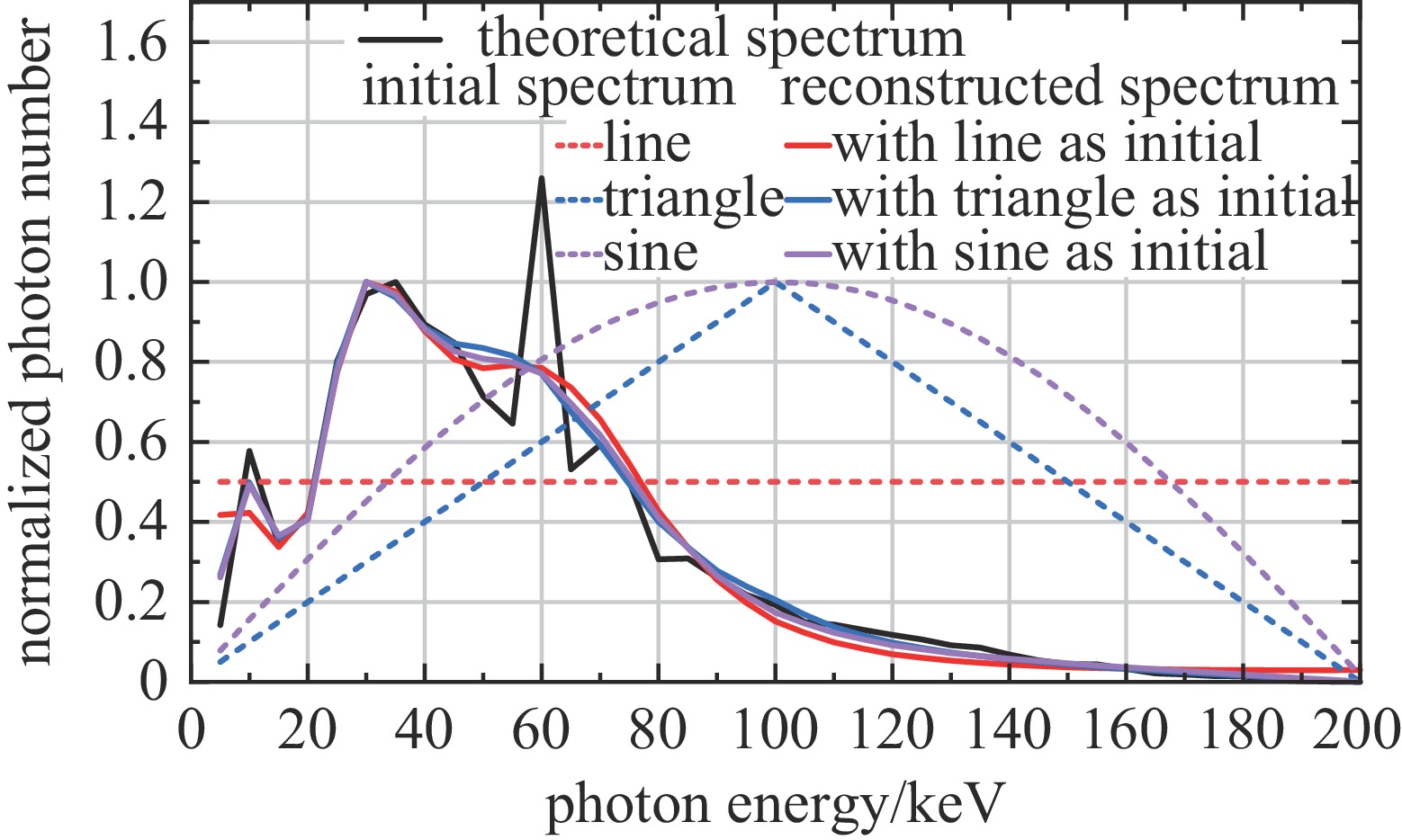
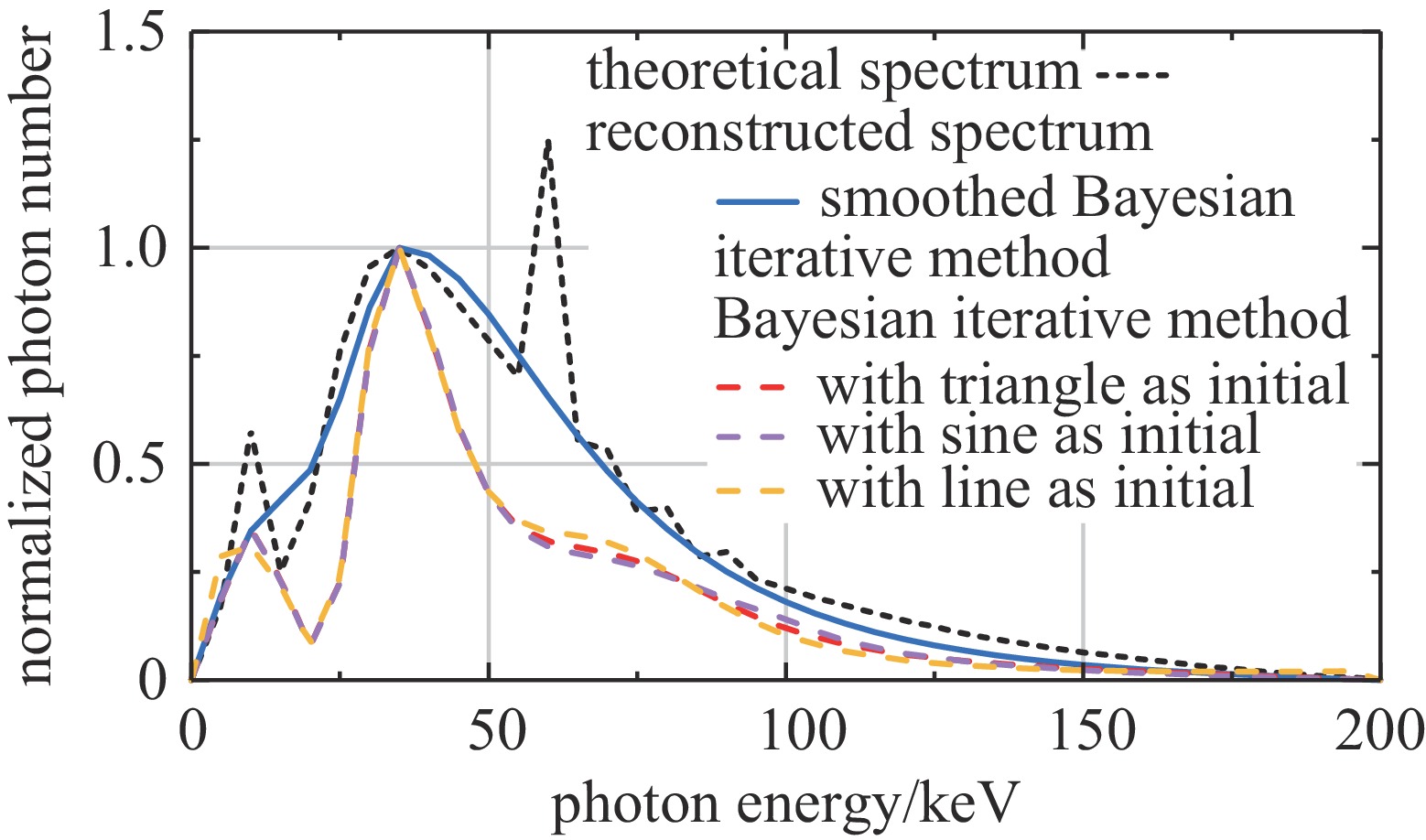
针对1.1节中给出的吸收片和探测器的材料和厚度,分别给定正弦波、三角形和直线三种初始能谱,依据探测器的理论沉积能量,利用迭代公式(2)重建能谱。设定当‖Φk+1−Φk‖2<10−6时迭代终止,得到按照最大值归一化后的重建能谱和理论能谱,如图3所示。
对比图3中三种初值的能谱重建结果和理论能谱得到,在除特征峰外的其他能段重建能谱与理论能谱基本吻合,说明初始谱对重建结果的影响较小。在特征峰附近,重建能谱的光子数目占比略有增加,但由于初始能谱和迭代方程中不包含特征峰信息,特征峰强度难以精确反映。
2. 重建能谱对干扰噪声的敏感度评估
2.1 评估方法
在实验测量能谱时,探测器的测量值不可避免地会受到测量系统底噪、光子散射噪声、环境噪声等多种干扰的影响,产生测量误差。对于高度病态的方程组(1),测量数据的误差会对解的准确度造成较大影响。为模拟实验中可能遇到的多种噪声,分别采用四种方式在1%、5%、10%三种噪声水平下生成随机噪声,添加在探测器的理论沉积能量中,模拟带有噪声的实际测量数据。利用贝叶斯迭代法分别对包含不同噪声的测量数据重建能谱,计算重建能谱和理论能谱的差异,评估重建能谱的准确度,从而评价能谱重建方法对噪声的敏感度。
对于由脉冲电压驱动、通过轫致辐射产生的脉冲X射线,当脉冲X射线最大能量为200 keV时,能量低于100 keV的光子占比超过90%,脉冲X射线与物品作用时,该范围内的光子占主导作用。因此,主要关注低于100 keV各能段的光子占比,选用该范围内重建能谱与理论能谱差的二范数‖ΔΦ‖2作为评价标准,‖ΔΦ‖2的数学表达式为
‖ΔΦ‖2=√[M/2]∑j=1(Φcj−Φtj)2 (3) 式中:Φcj表示第j个能段的重建能谱,Φtj表示第j个能段的理论能谱,M表示脉冲X射线能谱的能段个数。称‖ΔΦ‖2为重建能谱误差,‖ΔΦ‖2越小,重建能谱的准确性越高,噪声对重建能谱的影响越小。
分别对实验中可能出现的测量系统底噪、光子散射噪声、环境噪声、吸收片厚度误差四种干扰建立数值模拟模型,构成含噪声的沉积能量
${T'_{i1}} $ ~${T'_{i3}} $ 和含误差的吸收片厚度li′。其中,测量通道底噪以正比于沉积能量和沉积能量开方的两种高斯噪声之和的白噪声模拟[13, 22];光子散射噪声大多为正,以均值为1的正态分布模拟;环境噪声通过对各路沉积能量叠加幅度相同、均值为1的正态分布模拟,取探测器沉积能量的中位数T[N/2]作为环境噪声水平的计算依据,避免较小的信号被噪声淹没;吸收片厚度误差以高斯分布模拟,考虑测量误差的吸收片厚度li′由式(7)计算,根据扰动后li′计算得到能量沉积矩阵A′,依据探测器的理论沉积能量Ti重建能谱。式(4)~(7)为${T'_{i1}} $ ~${T'_{i3}} $ 和li′的计算公式。T′i1=Ti(1+γGi1+γiGi2) (4) T′i2=Ti[1+γ(Gi+1)] (5) T′i3=Ti+T[N/2]γ(Gi+1) (6) li′=li(1+γGi) (7) 式中:
$ {\gamma _i} = \gamma \sqrt {\dfrac{{{T_{\min }}}}{{{T_i}}}} $ ,Tmin为沉积能量的最小值,γ为噪声水平,Gi1和Gi2为服从高斯分布的随机数,即γGi1和γiGi2分别为与沉积能量、沉积能量的开方成正比的噪声;Gi为服从高斯分布的随机数;li为扰动前第i个通道的吸收片厚度。2.2 敏感度评估结果
基于2.1节中的评价方法,计算得到在正弦波、三角和直线三种初始能谱下,利用贝叶斯迭代法对不含噪声的探测器理论沉积能量的重建能谱误差‖ΔΦ‖2分别为0.58、0.58和0.64。采用2.1节中的四种噪声模拟方式,分别取1%、5%、10%三种噪声水平对测量数据随机扰动,得到重建能谱误差,如表1所示。由于噪声的随机性,在每种噪声水平下分别重复产生100组含噪声的测量数据,依次利用贝叶斯迭代法以直线作为初始能谱进行能谱重建。表1中为100组重建能谱误差‖ΔΦ‖2的平均值。
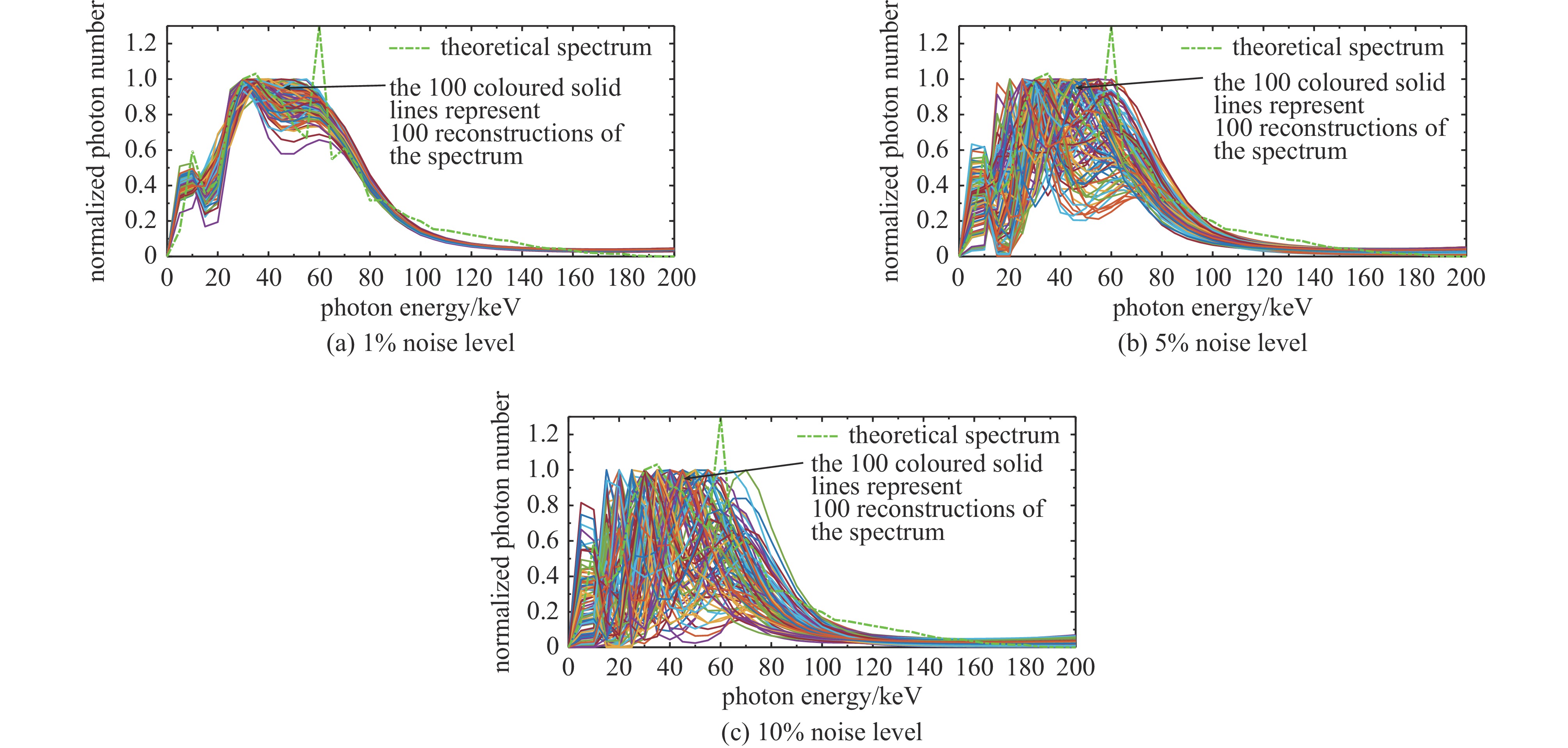
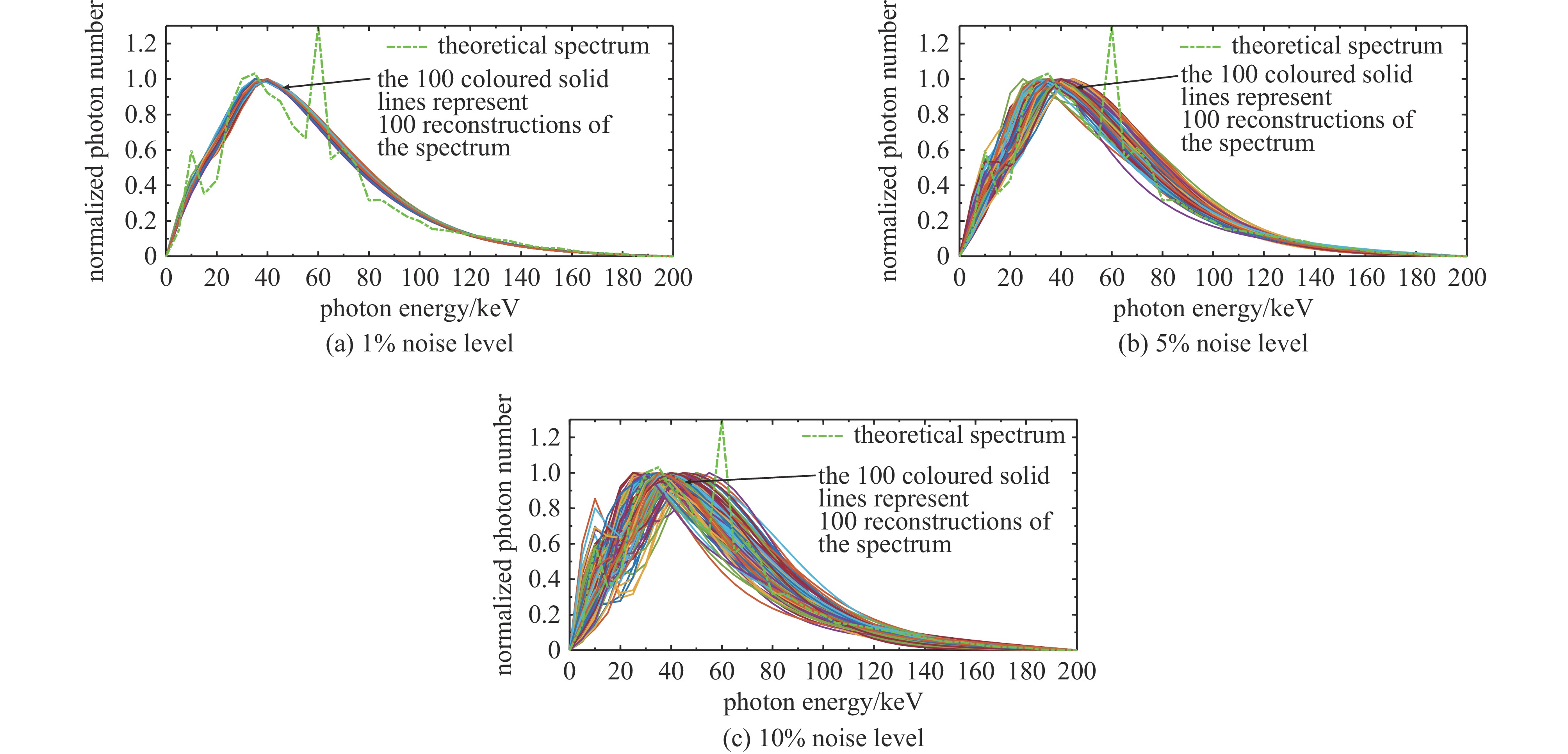
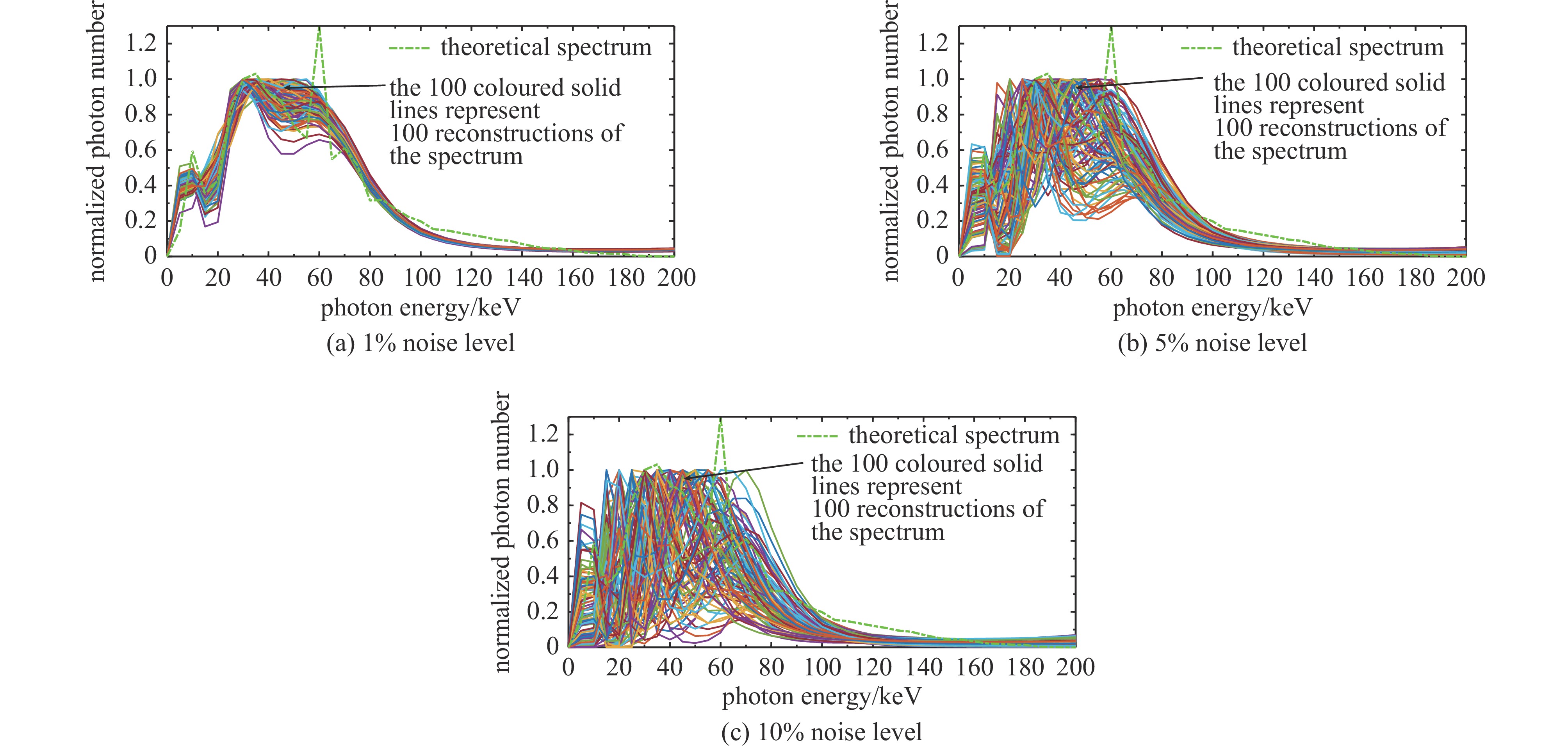
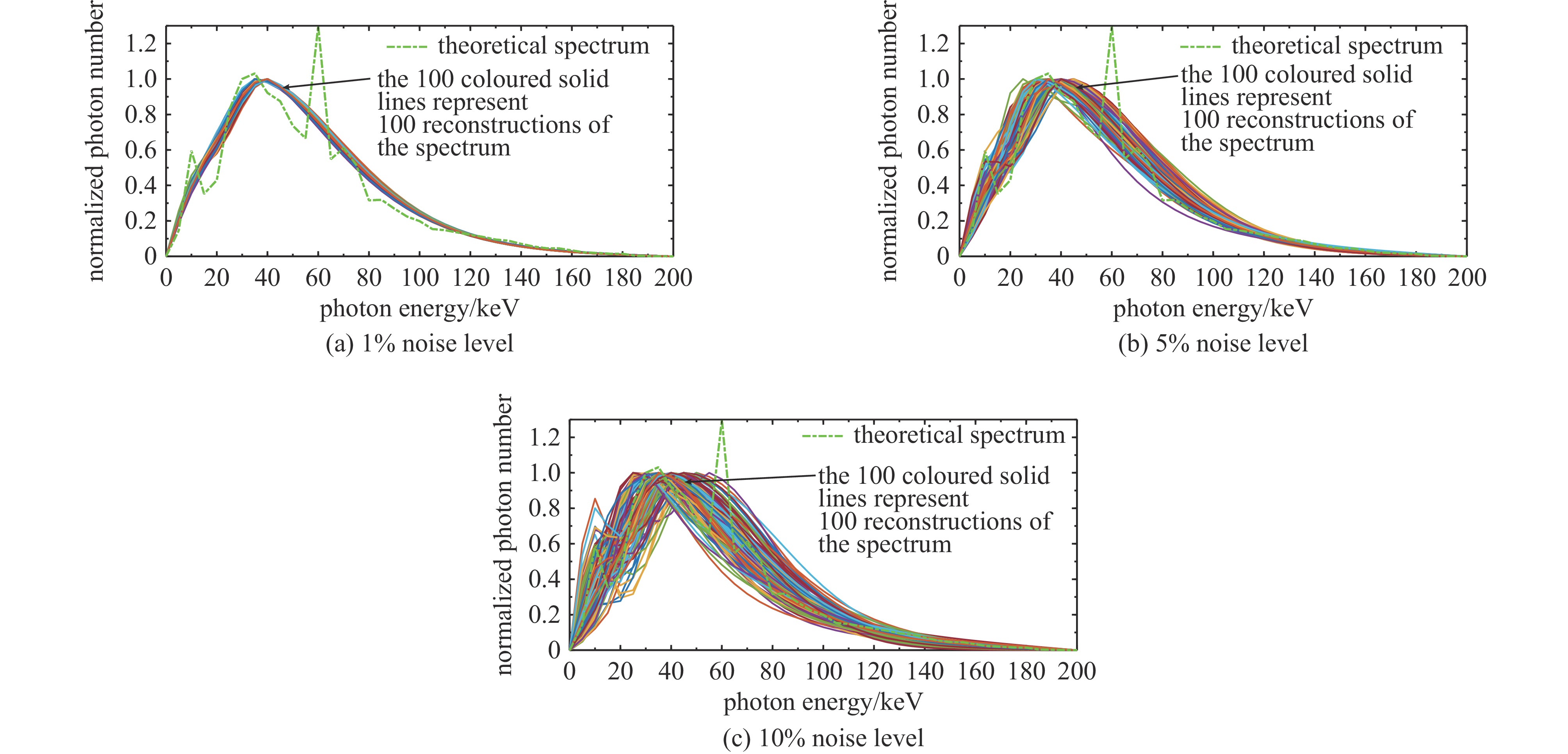
表 1 四种噪声扰动下贝叶斯迭代法重建能谱的平均误差Table 1. Average error of the spectrum reconstructed using the Bayesian iterative method, disturbed by four types of noisenoise type average error of the reconstructed spectrum $ \overline{ \left\| \Delta\mathit{\boldsymbol{\Phi\boldsymbol{ }}} \right\| _2} $ 1% noise level 5% noise level 10% noise level measurement system noise 0.68 1.10 1.53 photon scattering noise 0.68 1.02 1.42 environmental noise 0.65 0.81 1.01 absorption foil thickness error 0.66 0.87 1.31 由于计算重建能谱误差‖ΔΦ‖2时选用的理论能谱包含特征峰,而贝叶斯迭代法的重建能谱在特征峰附近有较大误差,因此无噪声时‖ΔΦ‖2约为0.6。由表1得到,当测量数据受到4种噪声1%噪声水平的扰动时,重建能谱误差‖ΔΦ‖2与无噪声时相近;随着噪声水平的提高,重建能谱误差‖ΔΦ‖2快速增长。以测量系统底噪为例,图4给出了在三种水平噪声扰动下的100次能谱重建结果,图中每条彩色实线代表一次重建能谱,绿色点划线为对比给出的理论能谱。结合表1和图4分析得到,当噪声水平1%时,重建能谱与理论能谱吻合较好,各次重建能谱间差异较小,噪声对重建能谱的影响小。当噪声水平达到5%时,在光子能量高于70 keV的高能部分,重建能谱与理论能谱基本吻合,低能部分各次重建能谱差异较大,噪声对重建能谱有较大影响。当噪声水平达到10%时,迭代过程中出现不收敛或收敛到局部最优的问题,部分重建能谱的能谱形状与理论能谱差异很大,重建能谱的分散性很大,此时,运用贝叶斯迭代法求解难以得到准确结果。实验测量中,不可避免引入多种噪声的干扰,导致测量数据中包含一定水平的噪声,影响能谱重建结果。因此,本文拟通过加入平滑系数的方式,降低能谱重建方法对噪声的敏感度。
3. 分段平滑的贝叶斯迭代法及噪声敏感度
3.1 加入平滑约束的贝叶斯迭代法
为解决高噪声水平时贝叶斯迭代法的重建能谱与理论能谱误差大的问题,在贝叶斯迭代法中加入平滑的约束条件。对于由轫致辐射产生的连续谱脉冲X射线,能谱在除特征峰外的其他能段平滑度较高,光子数目占比随能段的变化较为平稳。因此,加入平滑约束条件,平滑处理迭代后的能谱,作为下一次迭代的初始能谱,以降低重建能谱的随机性,提高准确度。
平滑处理时,每个能段的光子数目应包含相邻能段光子数目的信息,将第j个能段的光子数目按照式(8)的方式计算。对j−1和j+1能段的光子数目结合相应能段间的能量差加权处理,再与能段j的光子数目通过平滑系数加权计算,得到平滑后的光子数目。为避免平滑过程对平均能量的影响,平滑中j−1和j+1能段的权重相同,定义j−1和j+1能段的权重之和s2为平滑系数,s2∈[0,1]。平滑系数根据预估待测能谱的平滑程度调节,平滑系数越低,相邻能段占比越小,平滑程度越低;当s2=0时,无平滑效果。平滑过程中本能段光子数目的权重s1=1−s2。平滑处理中结合能谱的实际物理意义,设置最高和最低能段的光子数目为0,即边界条件为E0=0 keV,EN+1=Emax,Φ0=ΦN+1=0。
Φk+1j=s1Φkj+s22×Ej−Ej−1Ej+1−Ej−1Φkj−1+s22×Ej+1−EjEj+1−Ej−1Φkj+1 (8) 式中:Ej、Ej−1和Ej+1分别为第j、j−1和j+1个能段的能量,
${\mathit{\Phi}} _{j }^k $ 、${\mathit{\Phi}} _{j - 1}^k $ 和${\mathit{\Phi}} _{j + 1}^k $ 分别为第k次迭代后第j、j−1和j+1个能段的能谱,$ {\mathit{\Phi}} _j^{k + 1} $ 为平滑处理后的能谱,即第k+1次迭代中第j个能段起始能谱。3.2 分段平滑方法及平滑系数选取
平滑处理在降低迭代过程中随机性的同时,模糊了能谱中的一些细节信息。随着平滑系数的增加,被模糊近似的细节增多。当测量数据的噪声水平较低时,较高的平滑系数会使得能谱过度平滑,导致重建能谱的误差增加。因此,平滑系数根据预估能谱形状和吸收片的分辨能力确定。由于吸收片对不同能段光子的分辨能力不同,且不同能量范围内的能谱平滑程度略有差异,本节提出分段平滑的方法,在高能和低能部分采用不同的平滑系数,在降低随机性的同时避免过度平滑。
针对本文中研究的脉冲X射线能谱,结合图2吸收片对不同能段光子的分辨能力和图3的理论能谱可知,低能部分吸收片的分辨能力较强,能谱的平滑程度较低,因此选择较低的平滑系数s2=0.05;高能部分吸收片的分辨能量较弱,在不考虑特征峰时能谱的平滑程度较高,因此选择稍高的平滑系数s2=0.2。平滑过程中以光子数目最多的能段作为两种平滑系数选取的分界点。以1%、5%和10%三种噪声水平测量系统底噪的扰动为例,在每种水平的噪声下分别产生100组带有噪声的探测器沉积能量,利用整体平滑和分段平滑的贝叶斯迭代法依次重建能谱。将直线作为初始能谱,得到分别以s2=0.05和s2=0.2整体平滑和以低能部分s2=0.05、高能部分s2=0.2分段平滑的重建能谱误差‖ΔΦ‖2的平均值如表2所示。
表 2 不同平滑系数在测量系统底噪扰动下重建能谱的平均误差Table 2. Average error of the spectrum reconstructed with different smoothing coefficients, disturbed by measurement system noisereconstructed method average error of the reconstructed spectrum $ \overline{ \left\| \Delta\mathit{\boldsymbol{\Phi}} \right\| _2} $ 1% noise level 5% noise level 10% noise level segment smooth 0.748 0.752 0.763 smoothing coefficient s2=0.05 0.777 0.781 0.825 smoothing coefficient s2=0.2 0.740 0.754 0.812 表2重建能谱的误差表明,在噪声水平较低时(1%),重建能谱误差从小到大依次为:s2=0.2的整体平滑<分段平滑<s2=0.05的整体平滑,平滑系数越大,重建能谱误差越小。而当噪声水平较高时(5%或10%),分段平滑的重建能谱误差低于分别以两个平滑系数整体平滑的误差,分段平滑重建能谱的准确性更高,噪声敏感度更低。
3.3 分段平滑的贝叶斯迭代法对干扰噪声的敏感度评估
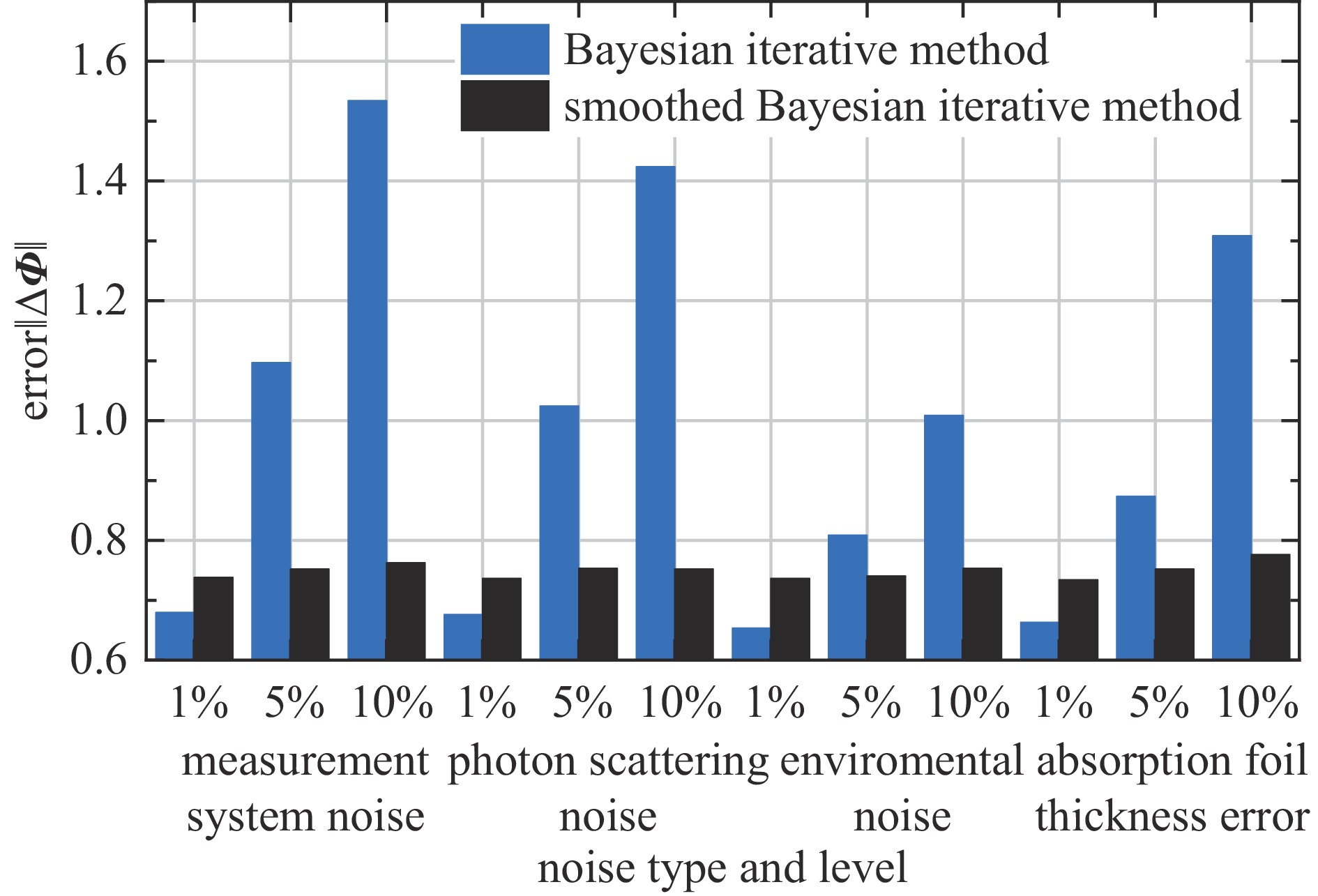
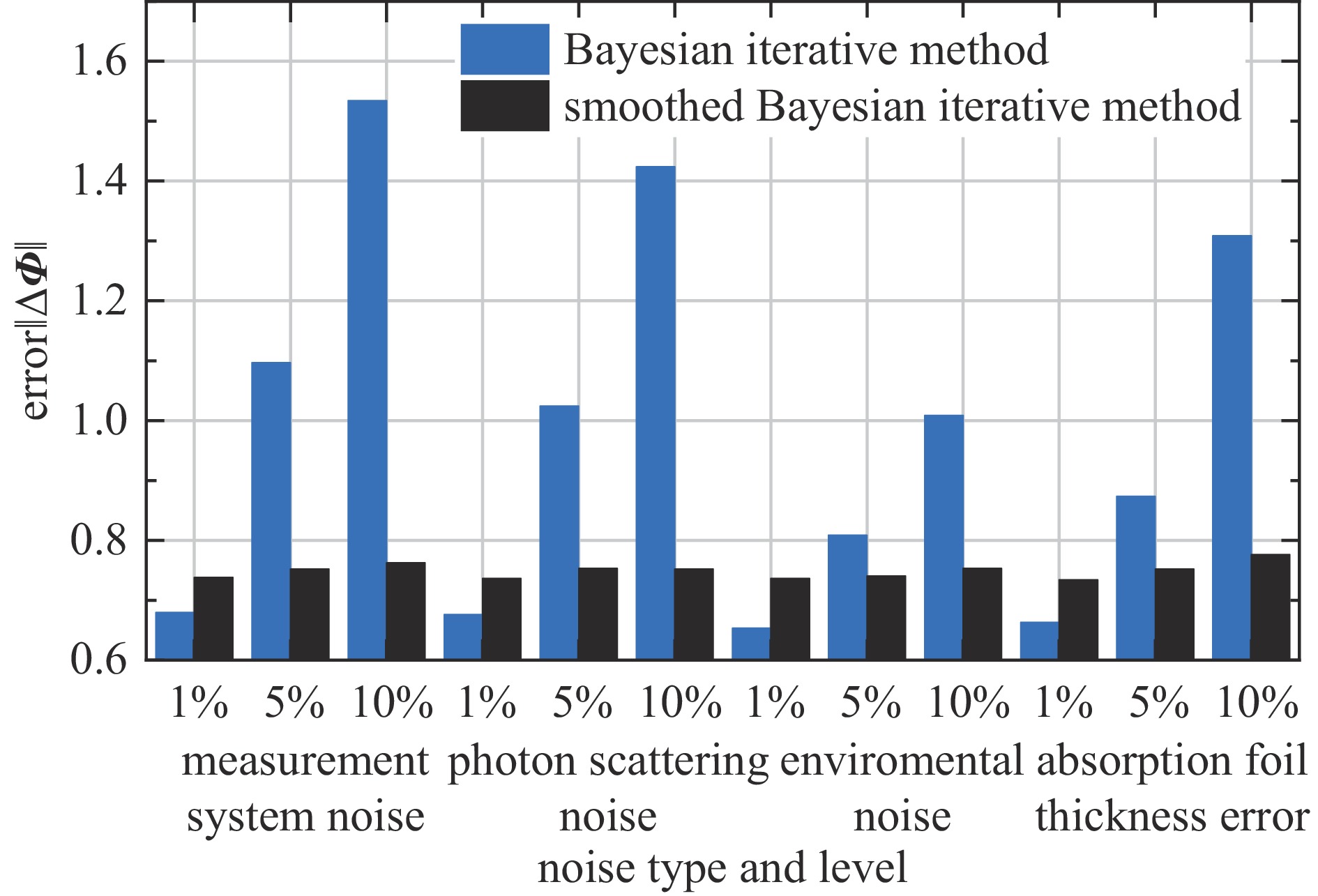
为评估分段平滑的贝叶斯迭代法对干扰噪声的敏感度,在探测器的理论沉积能量中分别加入测量系统底噪、光子散射噪声、环境噪声和吸收片厚度误差四种扰动,在1%、5%和10%三种噪声水平的干扰下,利用分段平滑的贝叶斯迭代法依次对含噪声的沉积能量重建能谱,选择直线作为初始能谱。每种噪声水平下重复100次,取100次重建能谱误差的平均值作为评价指标,如图5中黑色所示。分段平滑的贝叶斯迭代法的低能和高能部分平滑系数分别取0.05和0.2。
为清晰比较平滑效果,将贝叶斯迭代法的重建能谱误差在图5中以蓝色表示。当四种噪声的噪声水平为1%时,由于噪声水平较低,未加入平滑的贝叶斯迭代法的重建能谱中包含更多细节信息,重建能谱误差较小。而对于5%和10%的噪声水平,未加入平滑的贝叶斯迭代法重建能谱误差增长迅速,加入平滑约束后误差增长缓慢,始终保持在0.9以内。以测量系统底噪为例,图6给出了三种噪声水平的扰动下,加入平滑约束后的100次能谱重建结果(由100条彩色实线表示),图中绿色点划线为理论能谱。在三种噪声水平下,重建能谱的形状与理论能谱基本保持一致,相比平滑前的结果(图4),高噪声水平时重建能谱的随机性大幅降低。图5和图6说明,分段平滑的贝叶斯迭代法降低了重建能谱对测量数据噪声的敏感度,提高了噪声干扰下重建能谱的准确性。
4. 实验能谱重建及分析
实验测量的脉冲X射线由脉冲电子束入射20 μm的钽靶产生,脉冲电子束由峰值200 kV、半高宽30 ns的脉冲电压驱动等效阻抗2 Ω的二极管形成。针对待测脉冲X射线的能量范围,研制了基于吸收法的能谱测量系统,给出了有无平滑约束时贝叶斯迭代法的重建能谱,验证了平滑约束对重建能谱的改善效果。
4.1 能谱测量系统
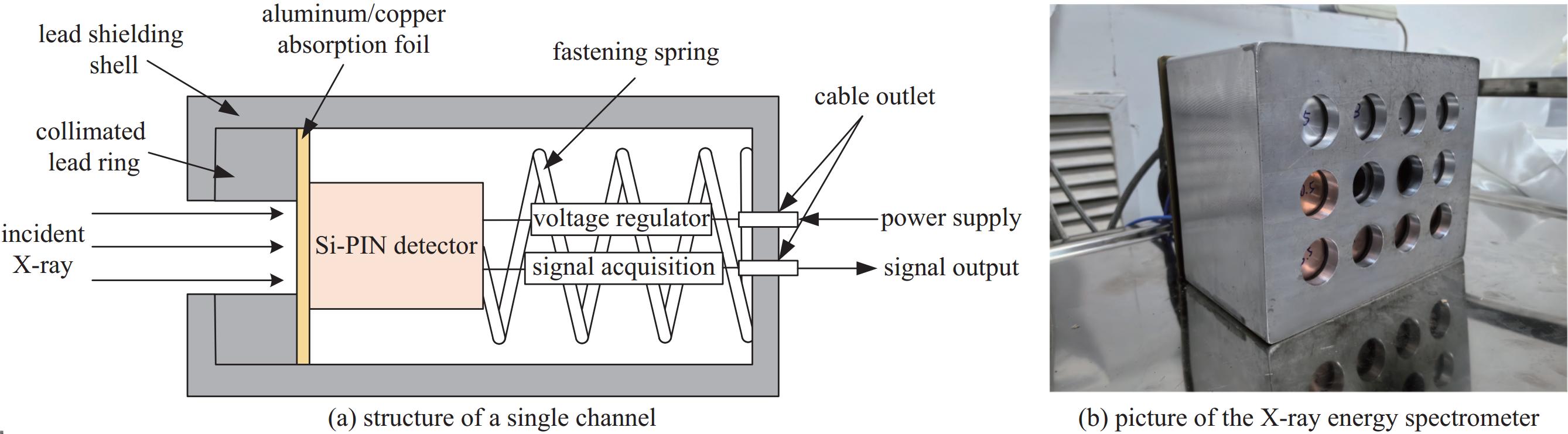
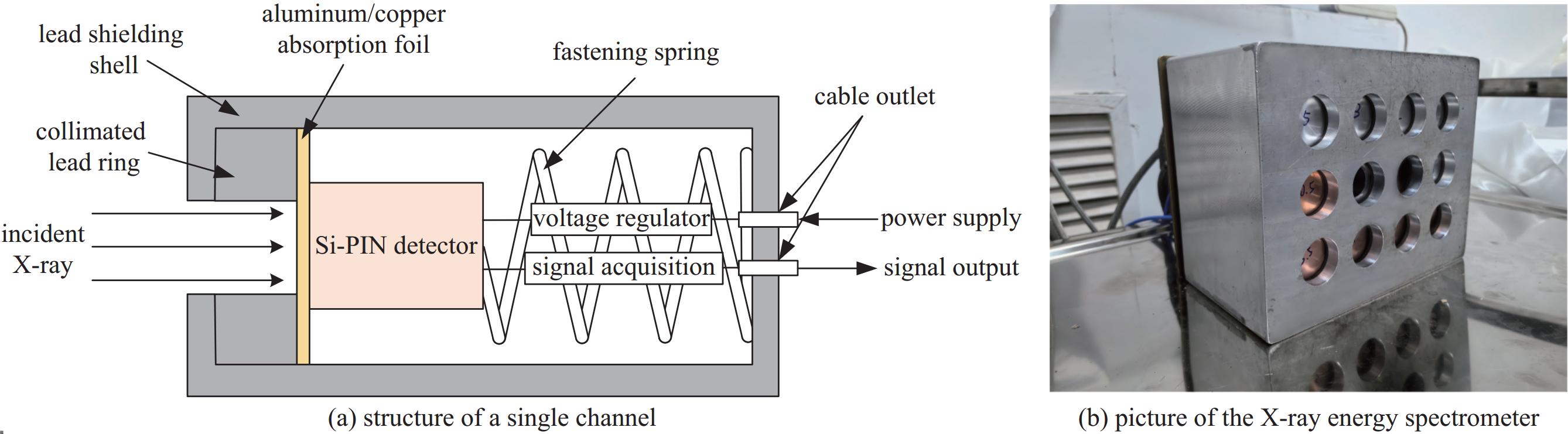
能谱测量系统包含11路测量通道,每路测量通道包括准直铅环、吸收片、Si-PIN探测器、探测器的稳压和信号采集模块、紧固弹簧、与供电和输出信号连接的电缆底座,如图7(a)所示。11路测量通道和1路备用通道以4×3的形式并列排列,放置于铅屏蔽壳内,测量系统实物图如图7(b)所示。探测器的迎光面垂直于脉冲X射线的入射方向,由紧固弹簧固定探测器的位置和方向。铅屏蔽外壳和准直铅环用于减少其他方向入射的脉冲X射线以及环境中的电磁干扰对探测器的影响。11路探测器为同一厂家同一批次生产,实验前标定11路探测器的一致性。用11路探测器测量相同的脉冲X射线信号,对输出波形积分,得到11路信号的误差小于0.3%,一致性较好。对每个吸收片的厚度多次测量取平均值,得到10个吸收片厚度分别为:铝吸收片厚0.96、1.97、3.00、4.89、7.93 mm,铜吸收片厚0.48、0.98、1.98、3.00、3.48 mm。
4.2 平滑前后的贝叶斯迭代法能谱重建结果
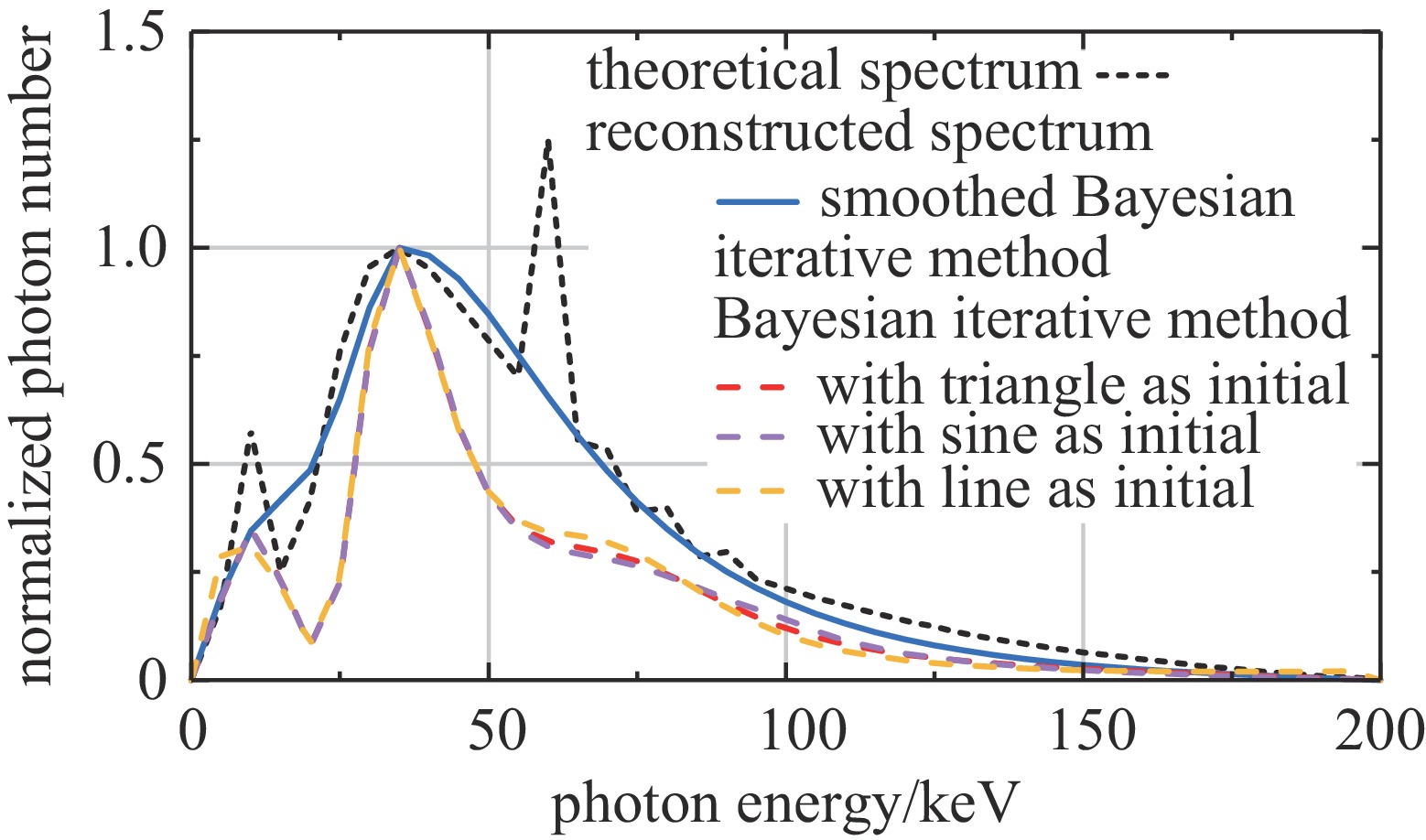
重建能谱时,由探测器输出波形的积分值表示光子在探测器上的能量沉积。依据11路测量数据,分别以正弦波、三角形、直线三种曲线作为初始能谱,用贝叶斯迭代法和分段平滑的贝叶斯迭代法重建能谱,得到归一化能谱如图8所示。图8中的理论能谱(黑色虚线)依据实测电压和电流波形计算得到。根据打靶的电子能量范围,光子的最高能量为200 keV,重建能谱时以5 keV为能段间隔,将能谱离散化为41个能段。对于分段平滑的贝叶斯迭代法,设定边界条件为:0 keV和200 keV能段的光子数目为0,低能和高能部分的平滑系数分别取0.05和0.2。
采用分段平滑的贝叶斯迭代法对实验能谱重建时,三种初始值重建得到的能谱相同,如图8中蓝色实线所示。分段平滑贝叶斯迭代法的重建能谱形状与理论能谱相近,由于初始能谱、迭代方程和平滑过程中不包含特征峰信息,在除特征峰外其他能段重建能谱与理论能谱基本吻合,重建能谱误差‖ΔΦ‖2=0.77,重建能谱平均能量为54.0 keV,与理论能谱的平均能量55.2 keV相近。未经平滑的贝叶斯迭代法对实验能谱重建时,三种初始能谱得到的结果相近,如图8中紫、红、黄三种颜色的虚线,与理论能谱形状差异较大。依据三种初始谱重建能谱的平均能量分别为53.4、53.6、53.6 keV,重建能谱误差‖ΔΦ‖2分别为1.43、1.47和1.45。综合能谱形状、平均能量、误差范数多种角度考虑,依据分段平滑的贝叶斯迭代法重建的实验能谱与理论值的吻合度更高,重建能谱的效果更优。
5. 结 论
本文通过在贝叶斯迭代法中加入平滑约束的方式,改善了重建能谱对测量数据噪声敏感的问题。根据预估待测能谱的特征,提出了以光子占比最多的能段为界分段平滑的方式,比较了分段平滑和整体平滑的能谱重建效果,并给出了平滑系数。对于实验中可能的误差来源,建立了测量系统底噪、光子散射噪声、环境噪声和吸收片厚度误差四种噪声的数值模拟方法,对比了在四种随机噪声、三种噪声水平(1%、5%和10%)的影响下,贝叶斯迭代法和分段平滑的贝叶斯迭代法的能谱重建效果。计算结果表明,加入平滑约束的贝叶斯迭代法对噪声的敏感度显著下降,重建能谱的随机性显著下降,准确度显著提升。设计了具有11路测量通道的能谱测量系统,验证了贝叶斯迭代法和分段平滑的贝叶斯迭代法对实验能谱的重建效果,实验结果表明,基于分段平滑的贝叶斯迭代法的重建能谱形状、平均能量均与理论能谱更接近,且重建能谱与理论能谱的误差小,重建能谱的效果更好。优化后的分段平滑贝叶斯迭代法对噪声的敏感度降低,对测量数据准确度的要求更低,可以用于处理包含较大噪声的测量信号,对于在复杂电磁环境中脉冲X射线能谱的重建具有重要意义。
致 谢 感谢程引会在本文的工作中给予的指导和帮助。
-
表 1 四种噪声扰动下贝叶斯迭代法重建能谱的平均误差
Table 1. Average error of the spectrum reconstructed using the Bayesian iterative method, disturbed by four types of noise
noise type average error of the reconstructed spectrum $ \overline{ \left\| \Delta\mathit{\boldsymbol{\Phi\boldsymbol{ }}} \right\| _2} $ 1% noise level 5% noise level 10% noise level measurement system noise 0.68 1.10 1.53 photon scattering noise 0.68 1.02 1.42 environmental noise 0.65 0.81 1.01 absorption foil thickness error 0.66 0.87 1.31 表 2 不同平滑系数在测量系统底噪扰动下重建能谱的平均误差
Table 2. Average error of the spectrum reconstructed with different smoothing coefficients, disturbed by measurement system noise
reconstructed method average error of the reconstructed spectrum $ \overline{ \left\| \Delta\mathit{\boldsymbol{\Phi}} \right\| _2} $ 1% noise level 5% noise level 10% noise level segment smooth 0.748 0.752 0.763 smoothing coefficient s2=0.05 0.777 0.781 0.825 smoothing coefficient s2=0.2 0.740 0.754 0.812 -
[1] Hill M A. The variation in biological effectiveness of X-rays and gamma rays with energy[J]. Radiation Protection Dosimetry, 2004, 112(4): 471-481. doi: 10.1093/rpd/nch091 [2] Suda Y, Hariu M, Yamauchi R, et al. Direct energy spectrum measurement of X-ray from a clinical linac[J]. Journal of Applied Clinical Medical Physics, 2021, 22(8): 255-264. doi: 10.1002/acm2.13354 [3] Hassan A I, Skalej M, Schlattl H, et al. Determination and verification of the x-ray spectrum of a CT scanner[J]. Journal of Medical Imaging, 2018, 5: 013506. [4] Duan Xinhui, Wang Jia, Yu Lifeng, et al. CT scanner x-ray spectrum estimation from transmission measurements[J]. Medical Physics, 2011, 38(2): 993-997. doi: 10.1118/1.3547718 [5] 苏兆锋, 杨海亮, 邱爱慈, 等. 高能脉冲X射线能谱测量[J]. 物理学报, 2010, 59(11):7729-7735 doi: 10.7498/aps.59.7729Su Zhaofeng, Yang Hailiang, Qiu Aici, et al. Measurements of energy spectra for high energy pulsed X-ray[J]. Acta Physica Sinica, 2010, 59(11): 7729-7735 doi: 10.7498/aps.59.7729 [6] Shafahi Z, Sina S, Faghihi R. Comparison of TSVD, MTSVD, and Tikhonov unfolding methods for reconstruction of X-ray spectra[J]. Radiation Physics and Chemistry, 2020, 166: 108437. doi: 10.1016/j.radphyschem.2019.108437 [7] 杨涛. 硬X射线能谱诊断技术[D]. 合肥: 中国科学技术大学, 2021: 41-72Yang Tao. Hard X-ray spectral diagnosis[D]. Hefei: University of Science and Technology of China, 2021: 41-72 [8] Li Fei, Ge Liangquan, Tang Zhuoyao, et al. Recent developments on XRF spectra evaluation[J]. Applied Spectroscopy Reviews, 2020, 55(4): 263-287. doi: 10.1080/05704928.2019.1580715 [9] Vanhoof C, Bacon J R, Fittschen U E A, et al. Atomic spectrometry update—a review of advances in X-ray fluorescence spectrometry and its special applications[J]. Journal of Analytical Atomic Spectrometry, 2021, 36(9): 1797-1812. doi: 10.1039/D1JA90033A [10] 王栋. 滤波-荧光法测量X光能谱的模拟计算[J]. 核电子学与探测技术, 2009, 29(4):773-778 doi: 10.3969/j.issn.0258-0934.2009.04.017Wang Dong. Analog computation of X-ray energy spectrum measurement with filter-fluorescence method[J]. Nuclear Electronics and Detection Technology, 2009, 29(4): 773-778 doi: 10.3969/j.issn.0258-0934.2009.04.017 [11] 苏兆锋, 孙江, 蔡丹, 等. 200 keV脉冲硬X射线源能谱测量技术[J]. 现代应用物理, 2022, 13: 030204, 030402Su Zhaofeng, Sun Jiang, Cai Dan, et al. Energy spectrum measurement for 200 keV pulsed hard X-ray source[J]. Modern Applied Physics, 2022, 13: 030204, 030402 [12] Endrizzi M, Delogu P, Oliva P. Application of an expectation maximization method to the reconstruction of X-ray-tube spectra from transmission data[J]. Spectrochimica Acta Part B: Atomic Spectroscopy, 2014, 102: 42-47. doi: 10.1016/j.sab.2014.10.009 [13] Manciu M, Manciu F S, Vulcan T, et al. Robust megavoltage x-ray spectra estimation from transmission measurements[J]. Journal of X-Ray Science and Technology, 2009, 17(1): 85-99. doi: 10.3233/XST-2009-0214 [14] Iwasaki S. A new approach for radiation inverse-problems based only on the Bayes' theory[C]//Proceedings of the 9th Workshop on Radiation Detectors and Their Uses. 1995. [15] Nauchi Y, Iwasaki S. Convergence of unfolded spectrum with response function for single radiation based on Bayes' theorem[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2014, 735: 437-443. doi: 10.1016/j.nima.2013.09.064 [16] Kobayashi M, Sato F, Kusaka S, et al. Feasibility study on real-time γ-ray spectrum/dose measurement system[J]. EPJ Web of Conferences, 2017, 153: 07014. doi: 10.1051/epjconf/201715307014 [17] Carasco C. Coupling gamma ray spectrometry and tomography in a Bayesian frame[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2021, 990: 164985. doi: 10.1016/j.nima.2020.164985 [18] Nishimura H, Shinohara M, Miyoshi T, et al. Experimental verification of real-time gamma-ray energy spectrum and dose monitor[J]. Applied Radiation and Isotopes, 2022, 185: 110226. doi: 10.1016/j.apradiso.2022.110226 [19] Mazrou H, Bezoubiri F. Evaluation of a neutron spectrum from Bonner spheres measurements using a Bayesian parameter estimation combined with the traditional unfolding methods[J]. Radiation Physics and Chemistry, 2018, 148: 33-42. doi: 10.1016/j.radphyschem.2018.02.014 [20] Takagi H, Murata I. Energy spectrum measurement of high power and high energy (6 and 9 MeV) pulsed X-ray source for industrial use[J]. Journal of Radiation Protection and Research, 2016, 41(2): 93-99. doi: 10.14407/jrpr.2016.41.2.093 [21] Takagi H, Murata I. Development of precise energy spectrum measurement technique for high-power pulsed X-ray sources for industrial use[J]. Journal of Nuclear Science and Technology, 2016, 53(6): 766-773. doi: 10.1080/00223131.2015.1072066 [22] 王继虎, 马文彦, 翁秀峰, 等. 期望最大法用于脉冲γ射线解谱的理论模拟与分析[J]. 现代应用物理, 2014, 5(3):169-173 doi: 10.3969/j.issn.2095-6223.2014.03.001Wang Jihu, Ma Wenyan, Weng Xiufeng, et al. Simulation and analysis of spectrum reconstruction of pulsed γ-rays using expectation maximization method[J]. Modern Applied Physics, 2014, 5(3): 169-173 doi: 10.3969/j.issn.2095-6223.2014.03.001 -





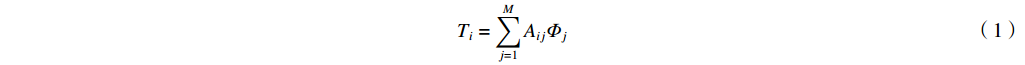

 下载:
下载:

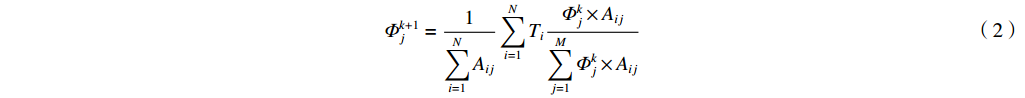

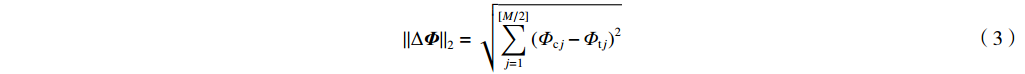
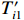
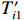
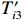
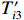
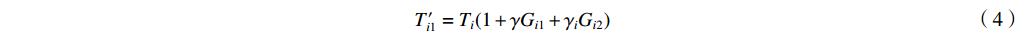
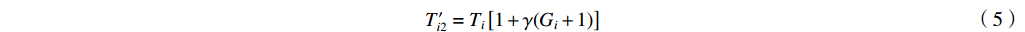
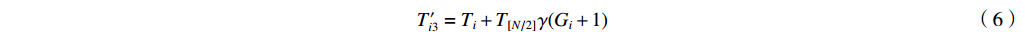
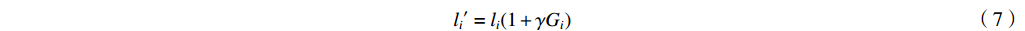
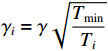

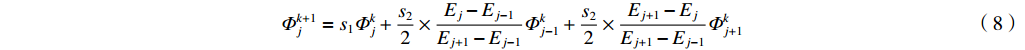
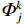
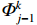
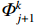
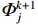




 下载:
下载: