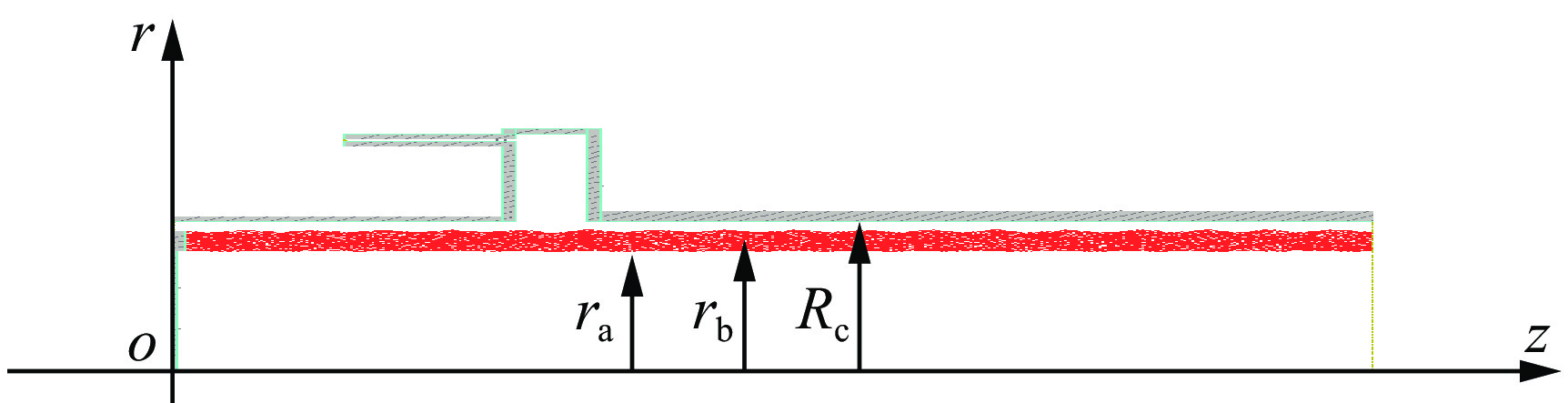
Matching theory and PIC simulation for klystron input cavity with beam
-
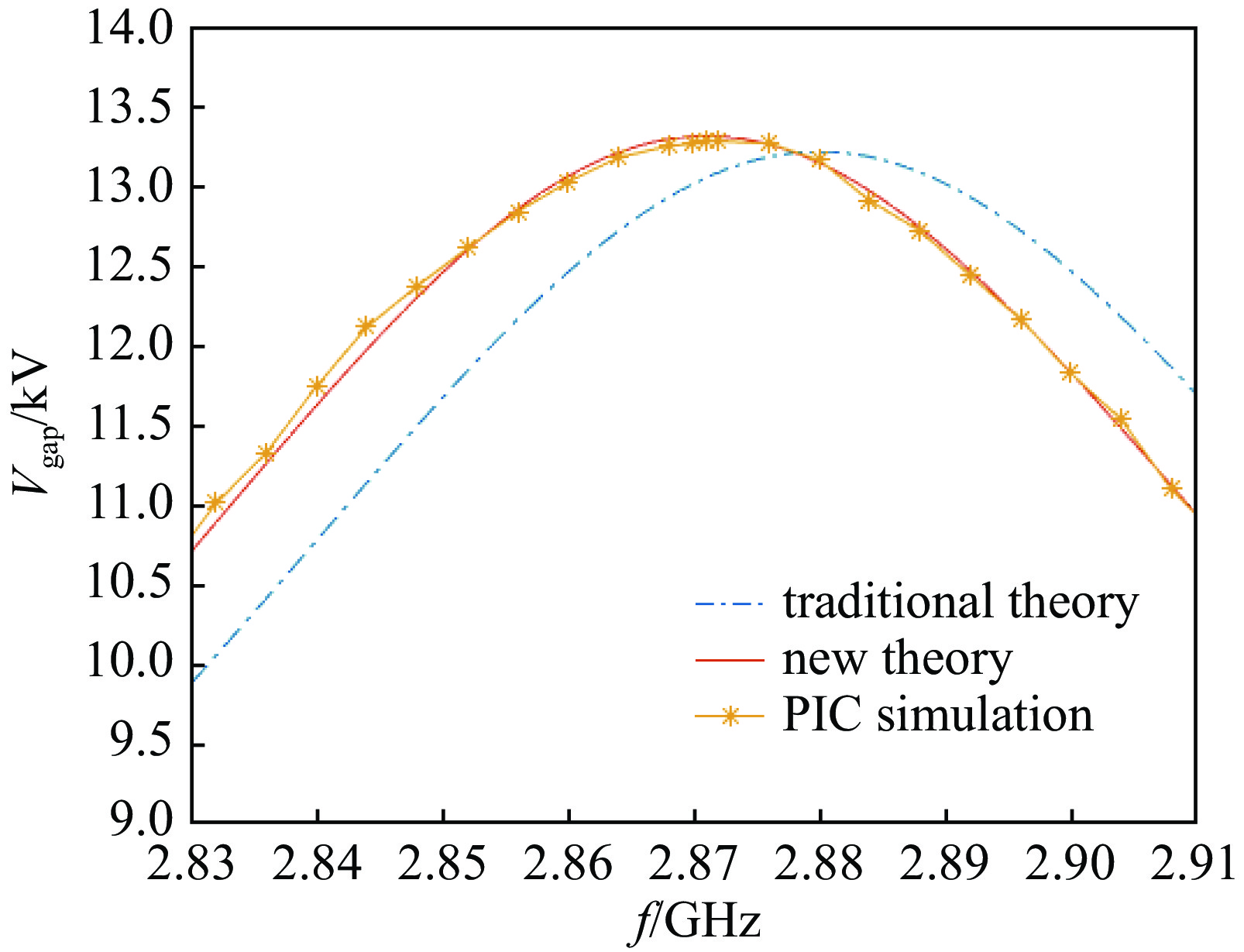
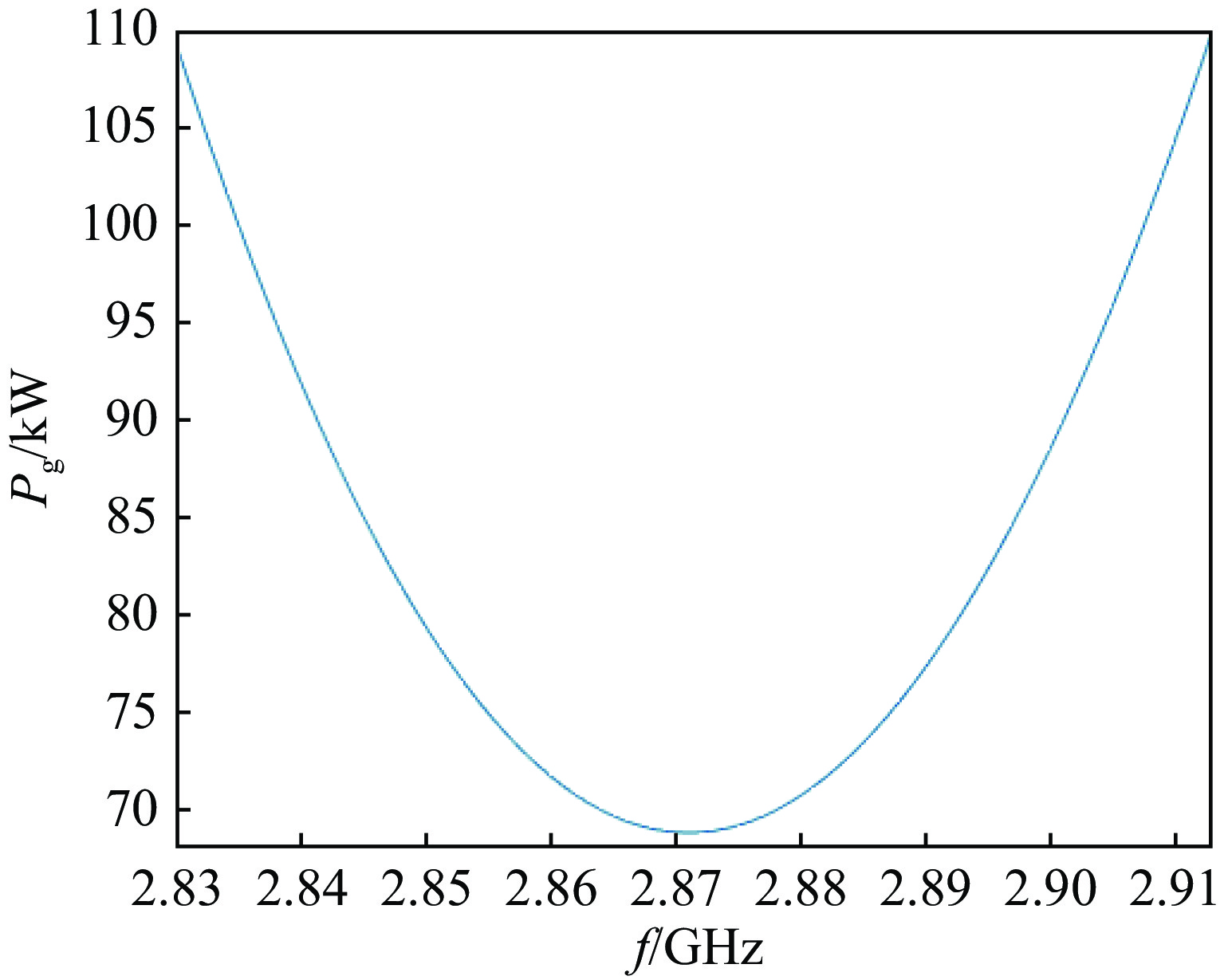
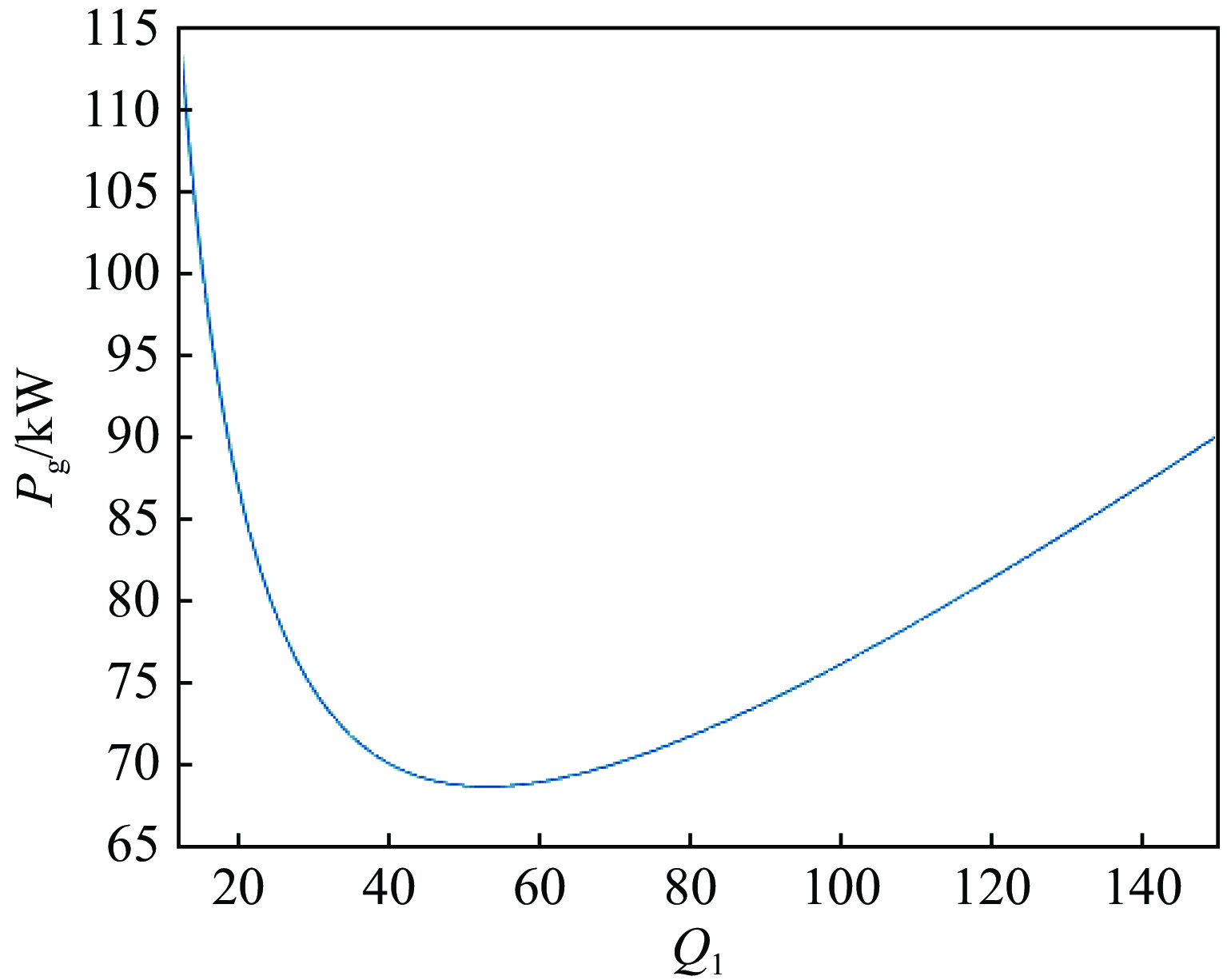
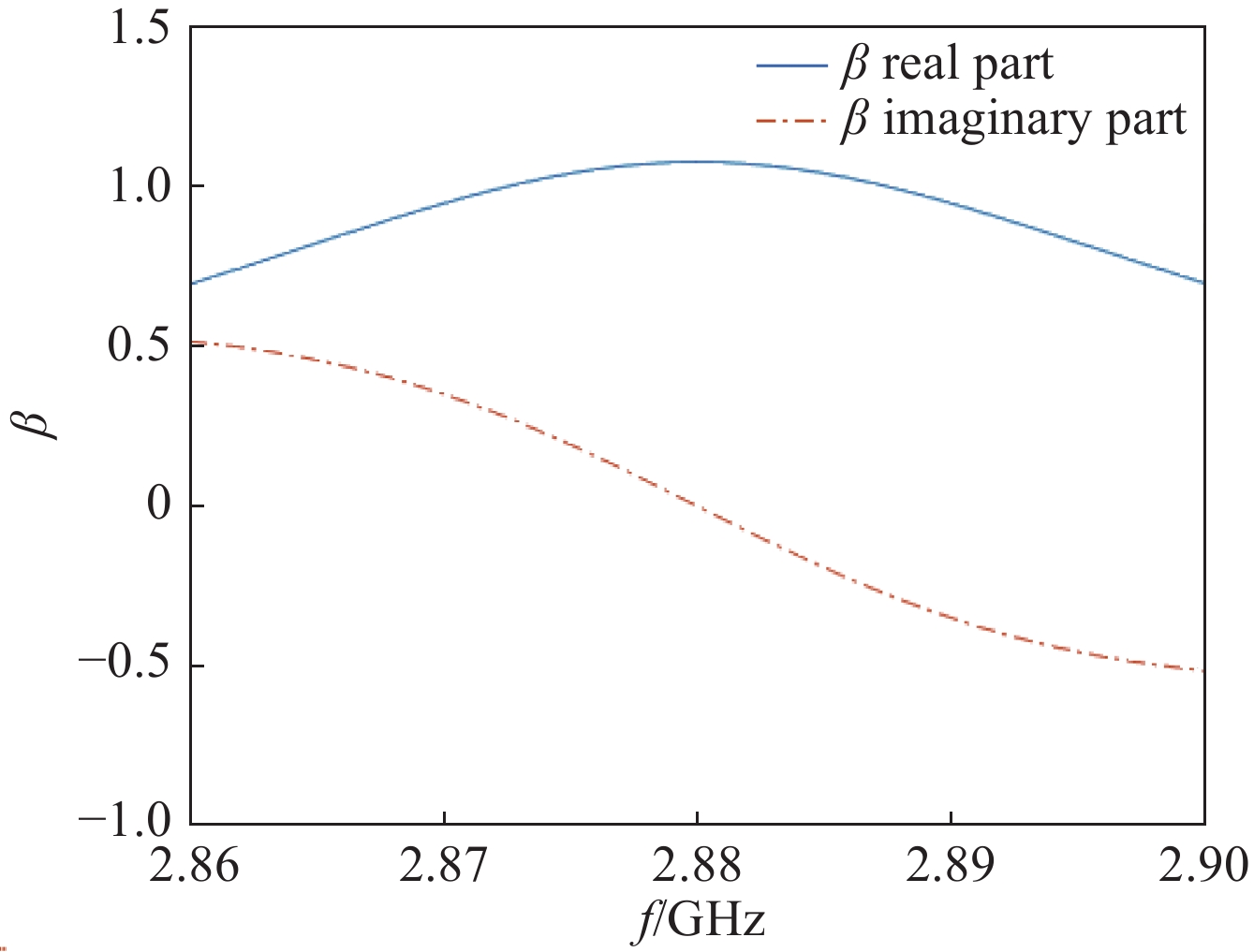
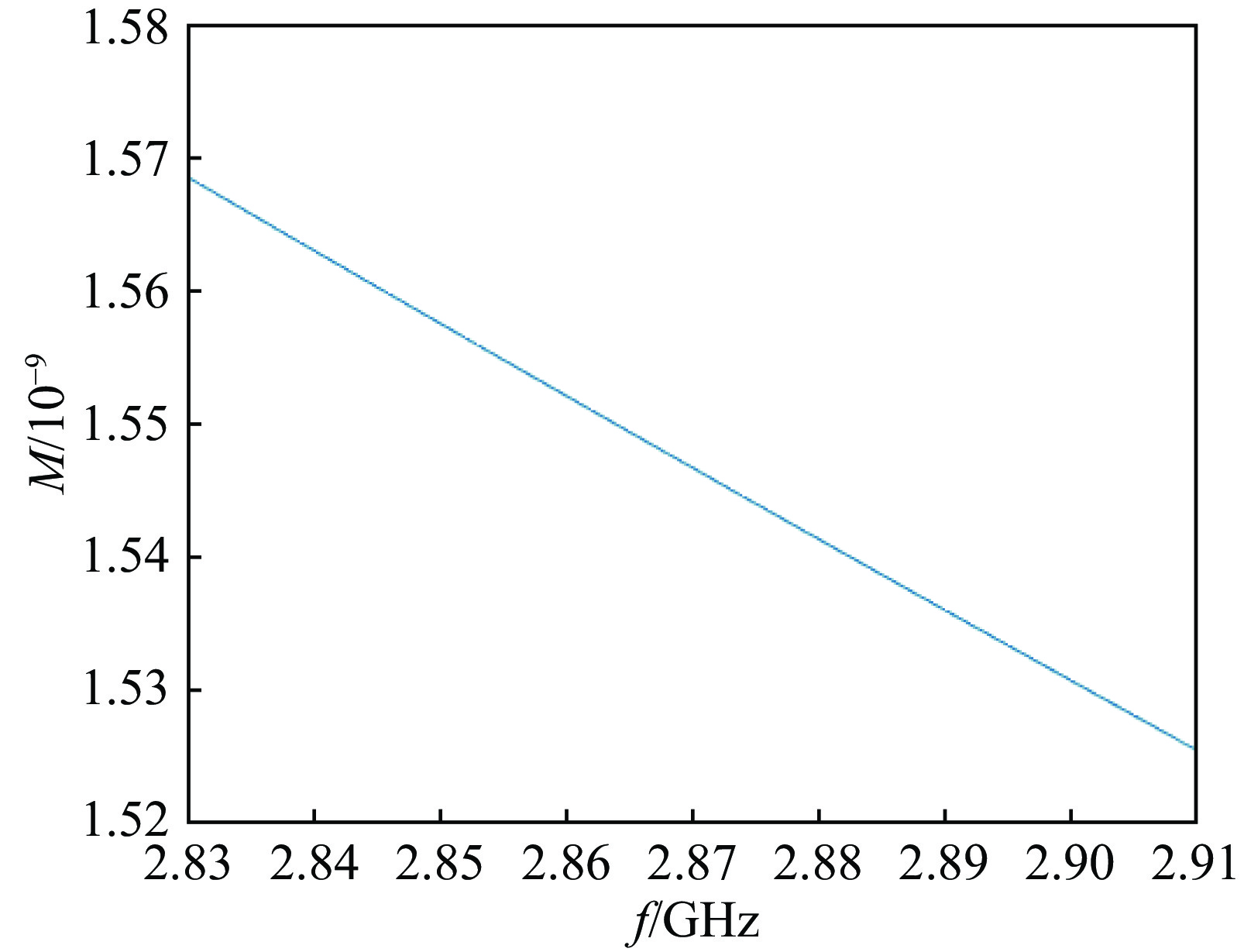
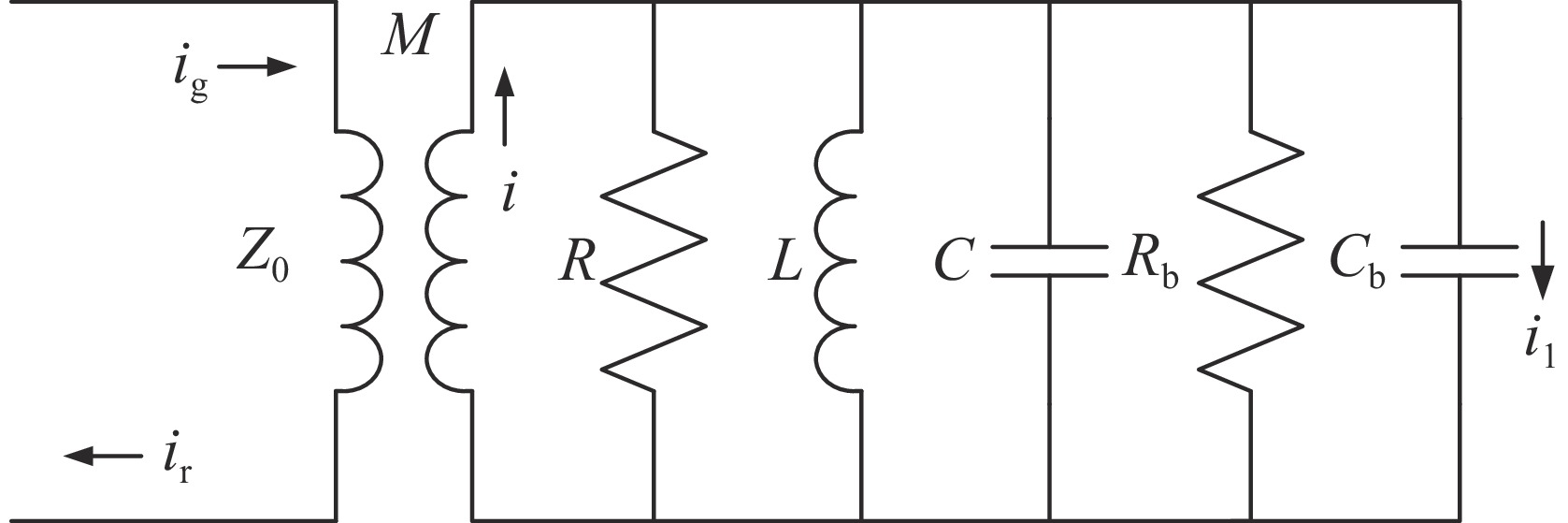
摘要: 基于输入微波与腔体耦合的等效电路模型，对于任意的腔体和电子束参数，建立了任意的输入微波与腔体耦合的速调管放大器输入腔的两种匹配状态的理论。建立了带有互感和电子束等效电阻和电容等参数的输入腔等效电路模型，推导了入射功率与反射功率的表达式，以及输入微波与带有电子束的输入腔耦合的完全匹配状态和任意的耦合这两种情形时输入功率和间隙电压关系的公式。推导了完全匹配状态时输入微波工作频率与输入腔有载品质因数的表达式。推导了复耦合系数等于1时输入腔外观品质因数与热腔品质因数的表达式，得出了当工作频率等于输入腔谐振频率，输入腔外观品质因数与热腔品质因数相等，且满足电子束等效电容远小于1时接近达到匹配状态，与传统理论基本一致。通过对比两种状态时的入射功率，得出了匹配状态时的入射功率小于复耦合系数等于1时入射功率的结论。通过对比复耦合系数等于1时新理论和传统理论的入射功率，得出不考虑电子束等效电容情况下两者相等的结论。采用二维粒子模拟的模型与匹配理论进行了对比，粒子模拟与理论基本一致。根据匹配理论找到了接近匹配状态的工作频率与有载品质因数以及较小的输入功率。Abstract: The matching theory based on a equivalent circuit model is outlined that self-consistently determines the modulation of a klystron input cavity for an arbitrary coupling of the input microwave to the cavity and arbitrary cavity parameters. The model including a mutual inductance and a beam equivalent capacitance and a equivalent resistance is established, and we find two expressions for the input power and the reflected power. We find an expression for the power required to maintain a desired cavity gap voltage for both the case when the coupling is perfectly matched to the input microwave, and also for case of arbitrary coupling. We find expressions for the frequency of the input microwave and externally-loaded Q leading to the matching condition. When the complex coupling coefficient equals 1, we find expressions for the beam-loaded Q and externally-loaded Q. We concluded that when the complex coupling coefficient equals 1,the operating frequency equals to the resonant frequency of the input cavity, the beam-loaded Q equals to externally-loaded Q, and the beam equivalent capacitance is much less than 1 will lead to the approximate matching condition. This conclusion is consistent with the traditional theory. By comparing the input power, We concluded that the input power corresponding to the matching condition is less than the input power corresponding to the approximate matching condition. When the complex coupling coefficient equals 1, by comparing the input power of the new theory and the traditional theory, we concluded that if the beam capacitance is neglected ,the input power corresponding to the new theory equals to the input power corresponding to the traditional theory. By the comparison of the 2D PIC simulation and the matching theory ,we can get the approximate value of the beam impedance. We find the frequency of the input microwave, the externally-loaded Q and the minimum input power according to the matching theory.
-
图 2 带有微波注入和电子束的速调管输入腔示意图
Figure 2. Schematic of a klystron input cavity with input microwave and beam
图 5 输入功率与有载品质因数关系图（间隙电压13.3 kV）
Figure 5. Input microwave power versus the externally-loaded Q
-
[1] 吴洋. 强流高增益相对论速调管放大器理论和实验研究[D]. 北京: 清华大学, 2012Wu Yang. Theoretical and experiment study on intense beam hign gain relativistic klystron amplifier[D]. Beijing: Tsinghua University, 2012 [2] Wu Yang, Xu Zhou, Jin Xiao, et al. A long pulse relativistic klystron amplifier driven by low RF power[J]. IEEE Transactions on Plasma Science, 2012, 40(10): 2762-2766. doi: 10.1109/TPS.2012.2210250 [3] Wu Yankai, Xie H Q, Li Z H, et al. Gigawatt peak power generation in a relativistic klystron amplifier driven by 1 kW seed-power[J]. Physics of Plasmas, 2013, 20: 113102. doi: 10.1063/1.4828975 [4] Carlsten B E, Ferguson P. Numerical determination of the matching conditions and drive characteristics for a klystron input cavity with beam[J]. IEEE Transactions on Electron Devices, 1997, 44(5): 894-900. doi: 10.1109/16.568055 [5] Carlsten B E, Faehl R J, Fazio M V, et al. Beam-cavity interaction physics for mildly relativistic, intense-beam klystron amplifiers[J]. IEEE Transactions on Plasma Science, 1994, 22(5): 730-739. doi: 10.1109/27.338289 [6] Wilsen C B, Luginsland J W, Lau Y Y, et al. A simulation study of beam loading on a cavity[J]. IEEE Transactions on Plasma Science, 2002, 30(3): 1160-1168. doi: 10.1109/TPS.2002.801623 [7] Carlsten B E, Ferguson P, Sprehn D. Accuracy of the equivalent circuit model using a fixed beam impedance for klystron gain cavities[J]. IEEE Transactions on Plasma Science, 1998, 26(6): 1745-1749. doi: 10.1109/27.747895 [8] 丁耀根. 大功率速调管的理论与计算模拟[M]. 北京: 国防工业出版社, 2008: 73-75Ding Yaogen. Theory and computer simulation of high power klystron[M]. Beijing: National Defence Industry Press, 2008: 73-75 [9] 何琥, 袁欢, 黄华. 相对论速调管放大器两腔束流调制的理论与模拟比较分析[J]. 强激光与粒子束, 2018, 30:053009He Hu, Yuan Huan, Huang Hua. A comparison between a self-consistent nonlinear theory of current modulation and 2D particle in cell simulation in two-cavity RKA[J]. High Power Laser and Particle Beams, 2018, 30: 053009 [10] 何琥, 戈弋, 袁欢, 等. 三腔整管RKA相位的理论与模拟的比较分析[J]. 强激光与粒子束, 2020, 32:103010 doi: 10.11884/HPLPB202032.200171He Hu, Ge Yi, Yuan Huan, et al. A comparison of phase between a nonlinear theory and 2D particle in cell simulation in three-cavity klystrons[J]. High Power Laser and Particle Beams, 2020, 32: 103010 doi: 10.11884/HPLPB202032.200171 -
下载:
点击查看大图
图(7)
计量
- 文章访问数: 45
- HTML全文浏览量: 25
- PDF下载量: 4
- 被引次数: 0
