Numerical simulation and measurement of two-dimensional thermal diffusion length under continuous heat loading
-
摘要: 热扩散系数是大能量、高功率激光系统中光学元件的重要参数，关系到元件的抗激光损伤性能，但现有热扩散系数测量方法在多维热传导情况下的测量结果误差较大，且热扩散长度是热扩散系数测量的基础，因此采用有限元法仿真了热源连续加热下的二维热传导并总结了热扩散长度与热扩散系数及加热时间之间的关系规律，据此提出了热源连续加热下测量二维热扩散长度的模型与方法。首先采用有限元分析建立模型仿真了一维热传导情况下的热扩散长度与热扩散系数的关系式并与数值解析表达式比较，二者符合较好，验证了使用连续热源与热扩散长度求解热扩散系数的可行性；之后扩展到二维热扩散情况，并讨论了热损失、样品厚度和热源加载时间对结果的影响；最后给出了实际测量方案，并给出提升测量精度措施。该工作为方便准确地测量材料或元件的热扩散长度提供思路，对制备高功率、大能量激光系统元件具有重要意义。Abstract: Thermal diffusion coefficient is an important parameter of optical components in high-energy and high-power laser systems, and it is related to the laser damage resistance of components. However, the measurement error of the existing thermal diffusion coefficient measurement methods is large under the condition of multi-dimensional thermal conduction. As thermal diffusion length is the basis of thermal diffusion coefficient measurement, our study used the finite element method to simulate the two-dimensional heat conduction under continuous heating of heat source, and summarized the relationship between thermal diffusion length, thermal diffusion coefficient and heating time. On this basis, it proposed a model and method for measuring two-dimensional thermal diffusion length under continuous heating of heat source. Firstly, finite element analysis was used to establish a model to simulate the relationship between thermal diffusion length and thermal diffusion coefficient in one-dimensional heat conduction, and the two models were compared with numerical analytical expressions. The feasibility of using continuous heat source and thermal diffusion length to solve the thermal diffusion coefficient was verified. The effects of heat loss, sample thickness and heat source loading time on the results were discussed. Finally, the practical measurement scheme and measures to improve the measurement accuracy were put forward. This study provides a way to measure the thermal diffusion length of materials or components conveniently and accurately, and is of great significance for fabrication of high power and high energy laser system components.
-
图 1 一维热绝缘仿真模型示意图
Figure 1. Schematic of the 1D thermal diffusion model under the continuous heat source
图 2 加载时间为10 s、热扩散系数为80 mm2/s时，无热损失的温度分布和表面温度场分布，以及不同热扩散系数下相应的LC和相对偏差δ1D
Figure 2. Loading time is 10 s, temperature distribution without heat loss and surface temperature field distribution when TDC is 80 mm2/s, and corresponding LC and corresponding relative deviation δ1D under different TDCs
图 3 考虑表面对流传热的一维热扩散模型示意图和热扩散系数为80 mm2/s、加载时间10 s时，不同厚度下温升沿x方向变化曲线
Figure 3. Schematic diagram of 1D thermal diffusion model considering surface convective heat transfer and when the TDC is 80 mm2/s and the loading time is 10 s, the temperature rise along the x direction under different thicknesses
图 4 当h=10 W/(m2·K)时，不同热源加载时间下一维热扩散模型的相对偏差结果
Figure 4. Relative deviation results of the 1D thermal diffusion model under different heat source loading times when h = 10 W/(m2·K)
图 5 半径为100 μm的连续热源作用下二维热扩散模型示意图
Figure 5. Schematic of the 2D thermal diffusion model under the continuous heat source with a radius of 100 μm
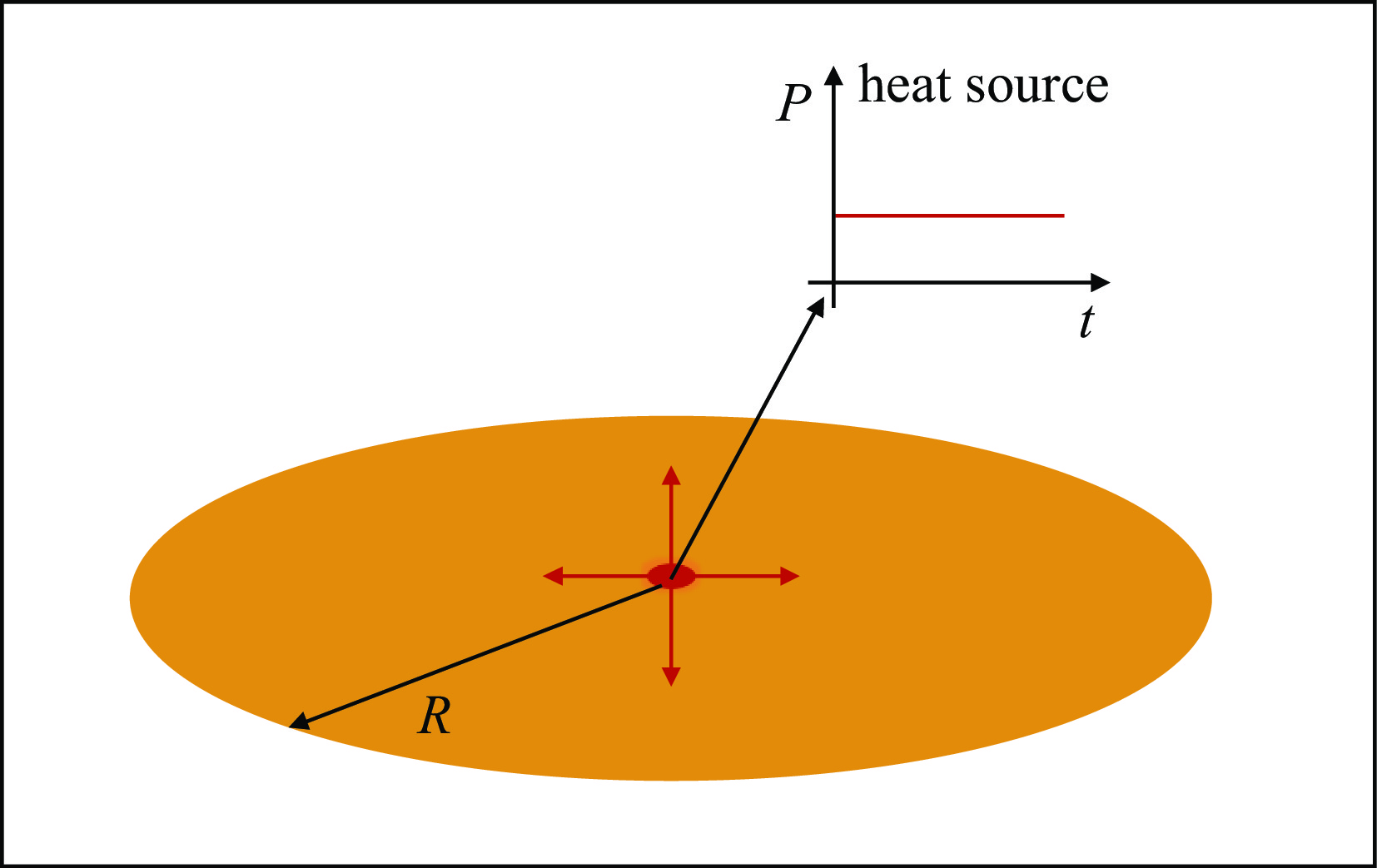
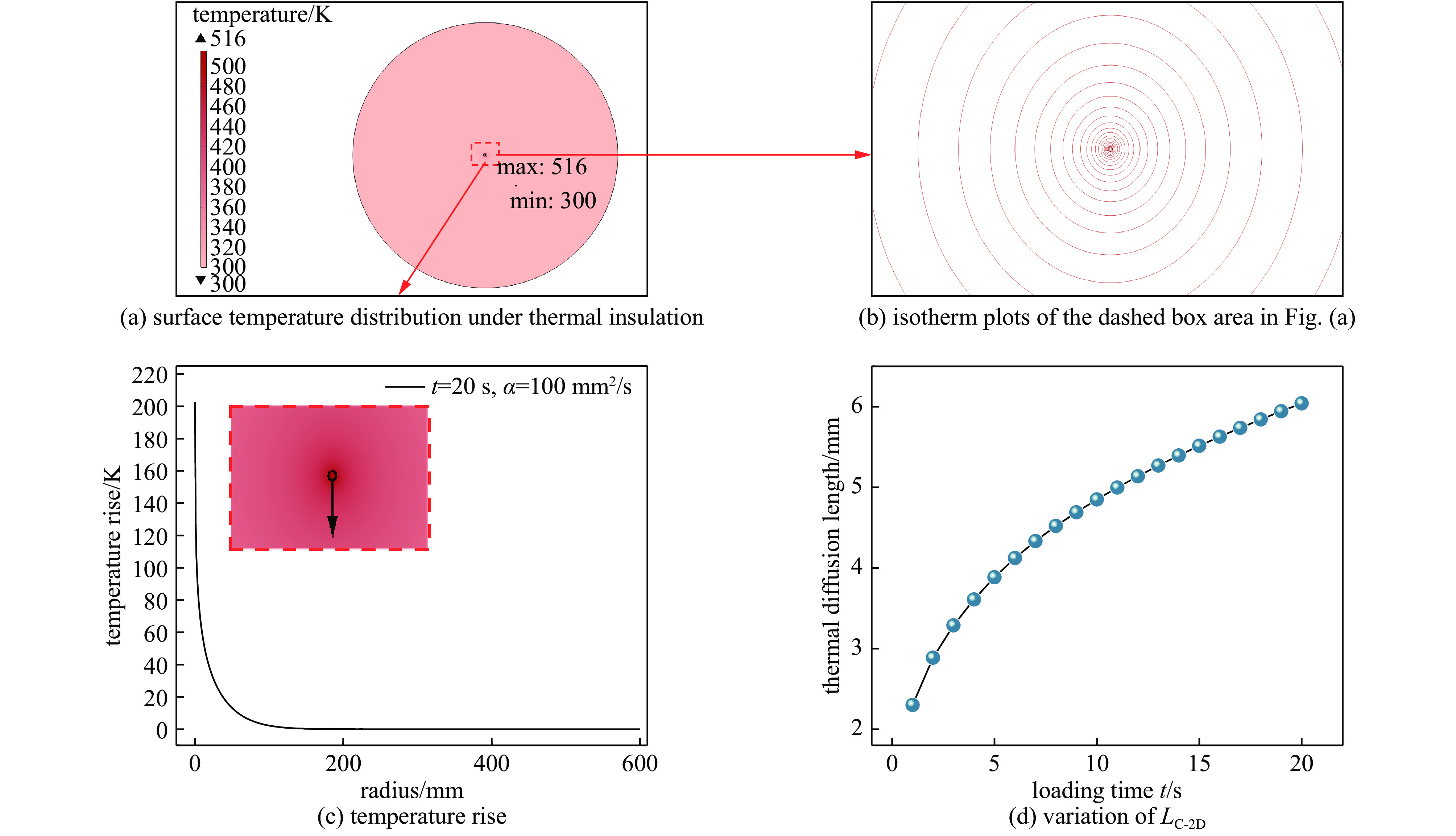
图 6 连续热源半径为100 μm、热扩散系数为100 mm2/s、加载时间为20 s时，绝热条件下的表面温度分布和图(a)所示虚线框区域的等温线图，以及温度从热源边缘沿径向上升和LC-2D随加载时间的变化
Figure 6. With a continuous heat source of radius 100 μm, TDC of 100 mm2/s, and loading time of 20 s, surface temperature distribution under thermal insulation, isotherm plots of the dashed box area in Fig.(a) and temperature rise along the radial direction from the edge of the heat source and variation of LC-2D with loading time
图 7 热扩散系数为100 mm2/s时，LC-2D与热源加载时间的拟合结果和A和α的拟合结果
Figure 7. Fitting result of LC-2D and heat source loading time when the TDC is 100 mm2/s, and coefficients A and α
图 8 不同热源加载时间下二维热扩散模型模拟的相对偏差结果
Figure 8. Relative deviation results of the 2D thermal diffusion model simulation under different heat source loading times
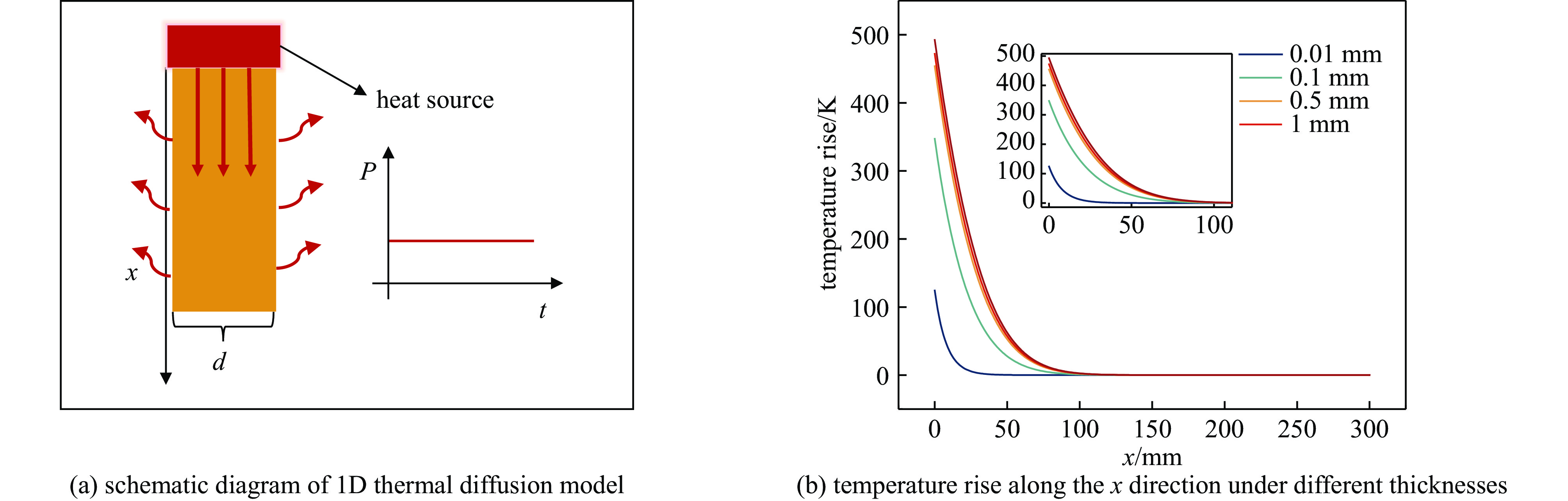
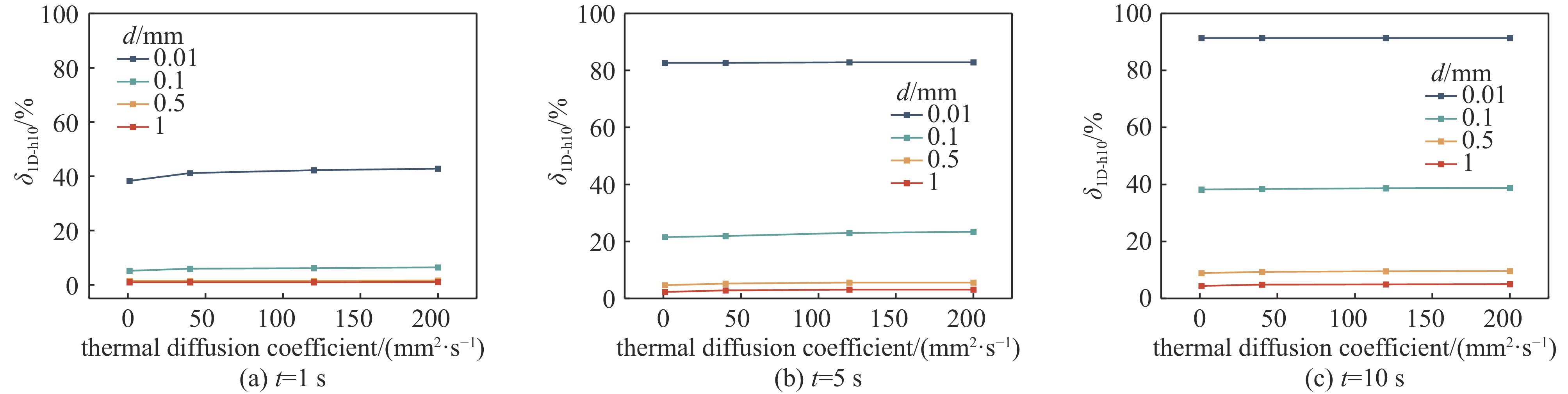
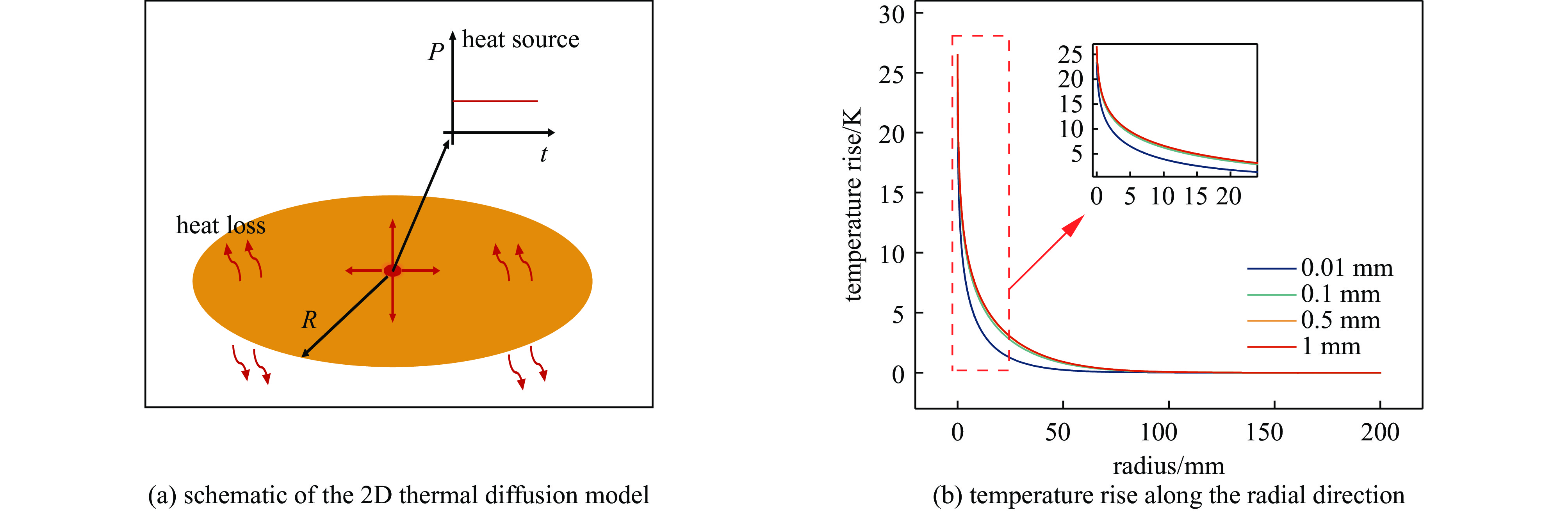
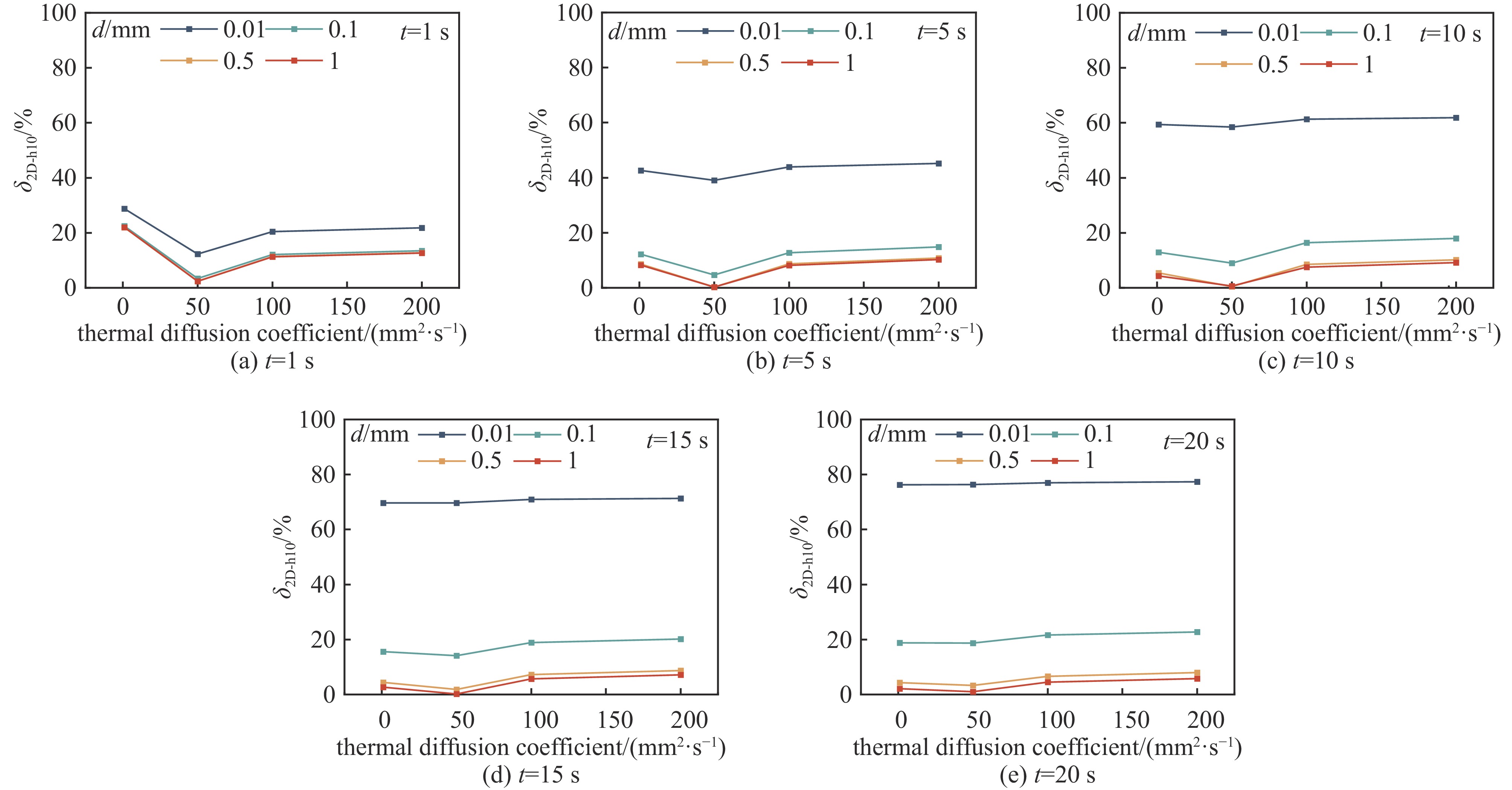
图 9 当h=10 W/(m2 K)时，半径为100 μm的连续热源的二维热扩散模型示意图和当热扩散系数为100 mm2/s，加载时间为20 s时，不同厚度下热源边缘沿径向的温升
Figure 9. Schematic of the 2D thermal diffusion model with a continuous heat source of a radius of 100 μm when h=10 W/(m2·K), and temperature rise along the radial direction from the edge of the heat source under different thicknesses when the TDC is 100 mm2/s and loading time is 20 s
图 10 当h=10 W/(m2·K)时，不同热源加载时间下二维热扩散模型的相对偏差结果
Figure 10. Relative deviation results of the 2D thermal diffusion model under different heat source loading times when h=10 W/(m2·K)
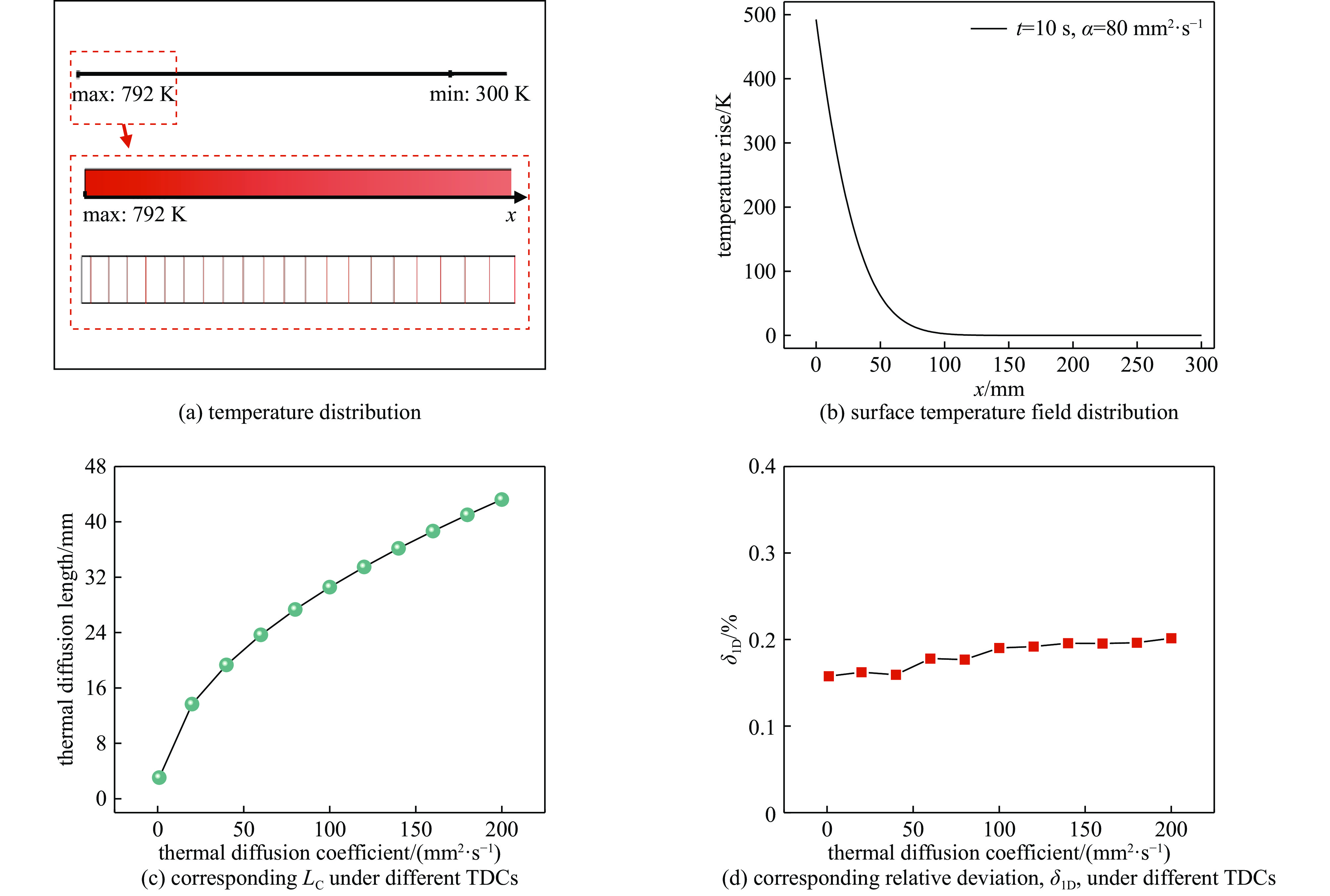
表 1 一维热扩散仿真参数
Table 1. 1D thermal diffusion model simulation parameters
model length/mm model thickness/mm heat source power
density/(W·cm−2)thermal diffusion
coefficient/(mm2·s−1)heat source loading
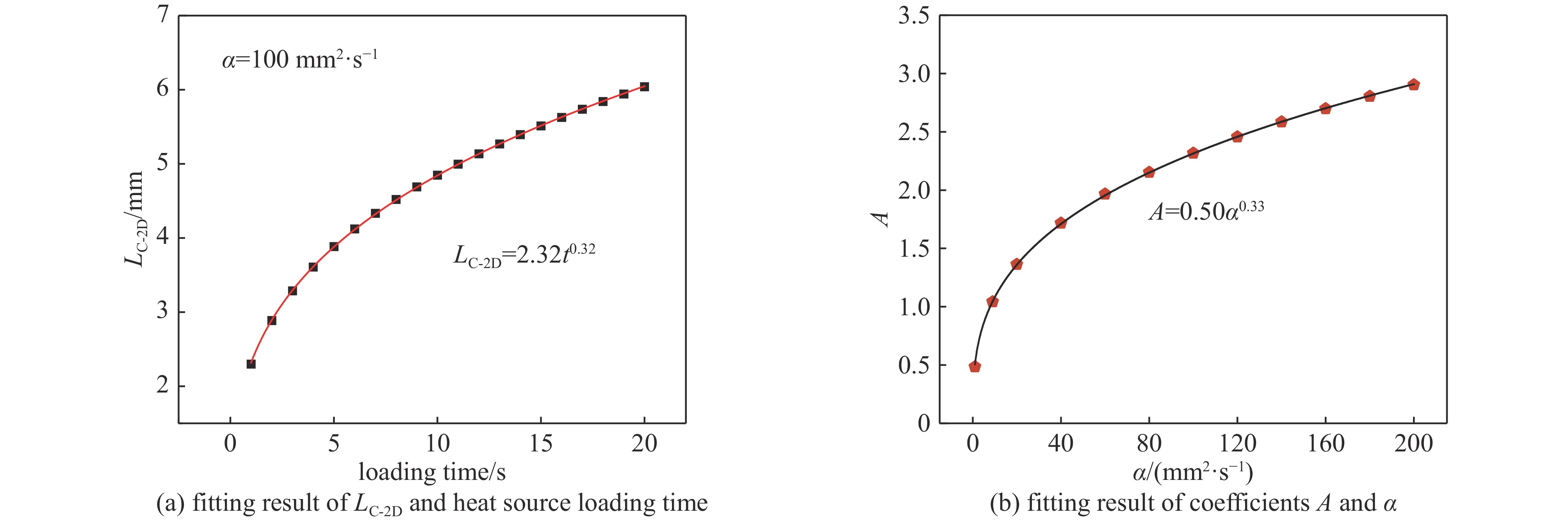
time/s500 0.5 200 1～200 0～10 
下载: 导出CSV
表 2 热扩散系数在 1～200 mm2/s内的拟合参数A和B
Table 2. Fitting results of A and B when the TDC ranges from 1～200 mm2/s
TDC/(mm2·s−1) A B 1 0.49 0.34 9 1.04 0.33 20 1.36 0.32 40 1.72 0.32 60 1.97 0.32 80 2.15 0.32 100 2.32 0.32 120 2.46 0.32 140 2.59 0.32 160 2.70 0.32 180 2.81 0.32 200 2.90 0.32
下载: 导出CSV
-
[1] Wan Hui, Cao Hao, Luan Shiyi, et al. Investigation of thermal damage in continuous wave laser-induced nanowelding[J]. Optics & Laser Technology, 2023, 161: 109143. [2] Boué C, Holé S. Infrared thermography protocol for simple measurements of thermal diffusivity and conductivity[J]. Infrared Physics & Technology, 2012, 55(4): 376-379. [3] Shen Pengfei, Zhuang Yangpeng, Jiang Shengda, et al. Experimental and numerical investigation on the ablation mechanism of Al2O3/Al2O3-CMCs under continuous-wave laser irradiation[J]. Journal of the European Ceramic Society, 2022, 42(5): 2307-2318. doi: 10.1016/j.jeurceramsoc.2022.01.005 [4] Sakai T, Okamoto Y, Taura N, et al. Effect of scanning speed on molten metal behaviour under angled irradiation with a continuous-wave laser[J]. Journal of Materials Processing Technology, 2023, 313: 117866. doi: 10.1016/j.jmatprotec.2023.117866 [5] Chen Zhao, Weng Yudong, Liu Junku, et al. Dual-band perfect absorber for a mid-infrared photodetector based on a dielectric metal metasurface[J]. Photonics Research, 2021, 9(1): 27-33. doi: 10.1364/PRJ.410554 [6] Chen Yan, Chen Kejian, Zhang Dajun, et al. Ultrabroadband microwave absorber based on 3D water microchannels[J]. Photonics Research, 2021, 9(7): 1391-1396. doi: 10.1364/PRJ.422686 [7] Wu C T, Yao M X, Dai T Y, et al. Thermal effect and laser characteristics of LD end-pumped CW Tm: YAG laser at room temperature[J]. Optik, 2017, 140: 356-362. doi: 10.1016/j.ijleo.2017.04.058 [8] Chen Guibo, Bi Juan. Semi-analytical simulation for temperature of material irradiated by CW laser considering the effect of atmospheric thermal blooming[J]. Optik, 2017, 130: 489-498. doi: 10.1016/j.ijleo.2016.10.071 [9] Lee K H, Shin W S, Kang E C. Analysis of optical damage in germanium induced by a continuous wave laser[J]. Applied Optics, 2013, 52(10): 2055-2061. doi: 10.1364/AO.52.002055 [10] Matthias E, Reichling M, Siegel J, et al. The influence of thermal diffusion on laser ablation of metal films[J]. Applied Physics A, 1994, 58(2): 129-136. doi: 10.1007/BF00332169 [11] Hofmeister A M. Dependence of heat transport in solids on length-scale, pressure, and temperature: implications for mechanisms and thermodynamics[J]. Materials, 2021, 14: 449. doi: 10.3390/ma14020449 [12] Li Yuxin, Yuan Hang, Dan Ziqiang, et al. Behavior analysis and threshold prediction of laser-induced damage in fused silica based on 2-D thermal diffusion model[J]. Ceramics International, 2024, 50(4): 7077-7085. doi: 10.1016/j.ceramint.2023.12.065 [13] Zhao Feiyun, Ren Aobo, Li Peihang, et al. Toward continuous-wave pumped metal halide perovskite lasers: strategies and challenges[J]. ACS Nano, 2022, 16(5): 7116-7143. doi: 10.1021/acsnano.1c11539 [14] Pierre T, Geslain É, Courtois M, et al. In-plane thermal diffusivity estimation by radial fin method[J]. Infrared Physics & Technology, 2022, 120: 103998. [15] Fabbri L, Fenici P. Three-dimensional photothermal radiometry for the determination of the thermal diffusivity of solids[J]. Review of Scientific Instruments, 1995, 66(6): 3593-3600. doi: 10.1063/1.1146443 [16] Pech-May N W, Mendioroz A, Salazar A. Simultaneous measurement of the in-plane and in-depth thermal diffusivity of solids using pulsed infrared thermography with focused illumination[J]. NDT & E International, 2016, 77: 28-34. [17] Bison P, Cernuschi F, Grinzato E. In-depth and in-plane thermal diffusivity measurements of thermal barrier coatings by IR camera: evaluation of ageing[J]. International Journal of Thermophysics, 2008, 29(6): 2149-2161. doi: 10.1007/s10765-008-0421-1 [18] Parker W J, Jenkins R J, Butler C P, et al. Flash method of determining thermal diffusivity, heat capacity, and thermal conductivity[J]. Journal of Applied Physics, 1961, 32(9): 1679-1684. doi: 10.1063/1.1728417 [19] Adamczyk W, Białecki R, Orlande H R B, et al. Nondestructive, real time technique for in-plane heat diffusivity measurements[J]. International Journal of Heat and Mass Transfer, 2020, 154: 119659. doi: 10.1016/j.ijheatmasstransfer.2020.119659 [20] Takahashi F, Hamada Y, Hatta I. Two-dimensional effects on measurement of thermal diffusivity by AC calorimetric method: III. advantage of double-heating method[J]. Japanese Journal of Applied Physics, 2000, 39: 6474. doi: 10.1143/JJAP.39.6474 [21] Huang Zhengxing, Tang Zhenan, Xu Ziqiang, et al. In-plane thermal diffusivity measurement of thin films based on the alternating-current calorimetric method using an optical reflectivity technique[J]. Chinese Physics Letters, 2004, 21(4): 713-715. doi: 10.1088/0256-307X/21/4/035 [22] Gu Yuqin, Hatta I. Development of ac calorimetric method for thermal diffusivity measurement IV: films with low thermal diffusivity and very thin films[J]. Japanese Journal of Applied Physics, 1991, 30: 1295. doi: 10.1143/JJAP.30.1295 [23] Hatta I, Sasuga Y, Kato R, et al. Thermal diffusivity measurement of thin films by means of an ac calorimetric method[J]. Review of Scientific Instruments, 1985, 56(8): 1643-1647. doi: 10.1063/1.1138117 [24] Zhang Xiang, Grigoropoulos C P. Thermal conductivity and diffusivity of free-standing silicon nitride thin films[J]. Review of Scientific Instruments, 1995, 66(2): 1115-1120. doi: 10.1063/1.1145989 [25] Siqueira M C, Maia R N A, Araujo R M T, et al. Determination of thermal and photothermal properties of an amorphous GaSe9 alloy[J]. Journal of Applied Physics, 2014, 116: 083514. doi: 10.1063/1.4894184 [26] Somer A, Camilotti F, Costa G F, et al. The thermoelastic bending and thermal diffusion processes influence on photoacoustic signal generation using open photoacoustic cell technique[J]. Journal of Applied Physics, 2013, 114: 063503. doi: 10.1063/1.4817655 [27] Nikolić P M, Todorović D M, Bojičić A I, et al. Transport properties of carriers in GaAs obtained using the photoacoustic method with the transmission detection configuration[J]. Journal of Physics: Condensed Matter, 1996, 8(30): 5673-5683. doi: 10.1088/0953-8984/8/30/016 [28] Calderón A, Muñoz Hernández R A, Tomás S A, et al. Method for measurement of the thermal diffusivity in solids: application to metals, semiconductors, and thin materials[J]. Journal of Applied Physics, 1998, 84(11): 6327-6329. doi: 10.1063/1.368957 [29] Todorović D M, Nikolić P M, Dramićanin M D, et al. Photoacoustic frequency heat-transmission technique: thermal and carrier transport parameters measurements in silicon[J]. Journal of Applied Physics, 1995, 78(9): 5750-5755. doi: 10.1063/1.359637 [30] 胡晨璐, 李大伟, 刘晓凤, 等. 利用表面热透镜方法测量光学元件热扩散率[J]. 中国激光, 2022, 49:2103101 doi: 10.3788/CJL202249.2103101Hu Chenlu, Li Dawei, Liu Xiaofeng, et al. Measuring thermal diffusivity of optical elements by surface thermal lens method[J]. Chinese Journal of Lasers, 2022, 49: 2103101 doi: 10.3788/CJL202249.2103101 [31] Younes J, Harajli Z, Soueidan M, et al. Mid-IR photothermal beam deflection technique for fast measurement of thermal diffusivity and highly sensitive subsurface imaging[J]. Journal of Applied Physics, 2020, 127: 173101. doi: 10.1063/1.5144174 [32] Amin-Chalhoub E, Semmar N, Coudron L, et al. Thermal conductivity measurement of porous silicon by the pulsed-photothermal method[J]. Journal of Physics D: Applied Physics, 2011, 44: 355401. doi: 10.1088/0022-3727/44/35/355401 [33] Dhouib A, Khalfaoui A, Bouaïcha M, et al. Investigation of thermal and optical properties on polysilicon by the photothermal deflection technique[J]. Journal of Applied Physics, 2018, 123: 161508. doi: 10.1063/1.4986514 [34] Jackson W B, Amer N M, Boccara A C, et al. Photothermal deflection spectroscopy and detection[J]. Applied Optics, 1981, 20(8): 1333-1344. doi: 10.1364/AO.20.001333 [35] Cernuschi F, Bison P G, Figari A, et al. Thermal diffusivity measurements by photothermal and thermographic techniques[J]. International Journal of Thermophysics, 2004, 25(2): 439-457. doi: 10.1023/B:IJOT.0000028480.27206.cb [36] Nagata S, Nishi T, Miyake S, et al. Development of novel thermal diffusivity analysis by spot periodic heating and infrared radiation thermometer method[J]. Materials, 2020, 13: 4848. doi: 10.3390/ma13214848 [37] Nolte P W, Malvisalo T, Wagner F, et al. Thermal diffusivity of metals determined by lock-in thermography[J]. Quantitative InfraRed Thermography Journal, 2017, 14(2): 218-225. doi: 10.1080/17686733.2017.1329777 [38] Bertolotti M, Fabbri L, Sibilia C, et al. Photothermal deflection applied to thermal diffusivity measurements of ceramic (ferrite) materials[J]. Journal of Physics D: Applied Physics, 1988, 21(10S): S14-S16. doi: 10.1088/0022-3727/21/10S/005 [39] Jeon P, Lee K, Yoo J, et al. Measurement of thermal diffusivity using deformation gradient and phase in the photothermal displacement technique[J]. KSME International Journal, 2003, 17(12): 2078-2086. doi: 10.1007/BF02982448 [40] Mendioroz A, Fuente-Dacal R, Apiñaniz E, et al. Thermal diffusivity measurements of thin plates and filaments using lock-in thermography[J]. Review of Scientific Instruments, 2009, 80: 074904. doi: 10.1063/1.3176467 [41] Doualle T, Le Guillous V, Klosek V, et al. Development of UO2 thermal diffusivity measurement with laser techniques[J]. EPJ Web of Conferences, 2021, 253: 07005. doi: 10.1051/epjconf/202125307005 [42] Salazar A, Oleaga A, Mendioroz A. How far and fast does heat propagate?[J]. Latin-American Journal of Physics Education, 2019, 13: 2307. [43] 范树海. 高灵敏度光学薄膜弱吸收测量仪的研制[D]. 上海: 中国科学院上海光学精密机械研究所, 2005: 46-48Fan Shuhai. High sensitive weak absorption apparatus for optical coatings[D]. Shanghai: Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, 2005: 46-48 [44] 王忆楠. 飞行器舱内热分析等效热沉法与对流换热系数辨识研究[D]. 哈尔滨: 哈尔滨工业大学, 2023Wang Yi’nan. Equivalent heat sink method and identification of convective heat transfer coefficient for thermal analysis in aircraft cabins[D]. Harbin: Harbin Institute of Technology, 2023 -
点击查看大图
计量
- 文章访问数: 149
- HTML全文浏览量: 45
- PDF下载量: 13
- 被引次数: 0
