Method for solving Vlasov equation based on physical informed Fourier neural operator
-
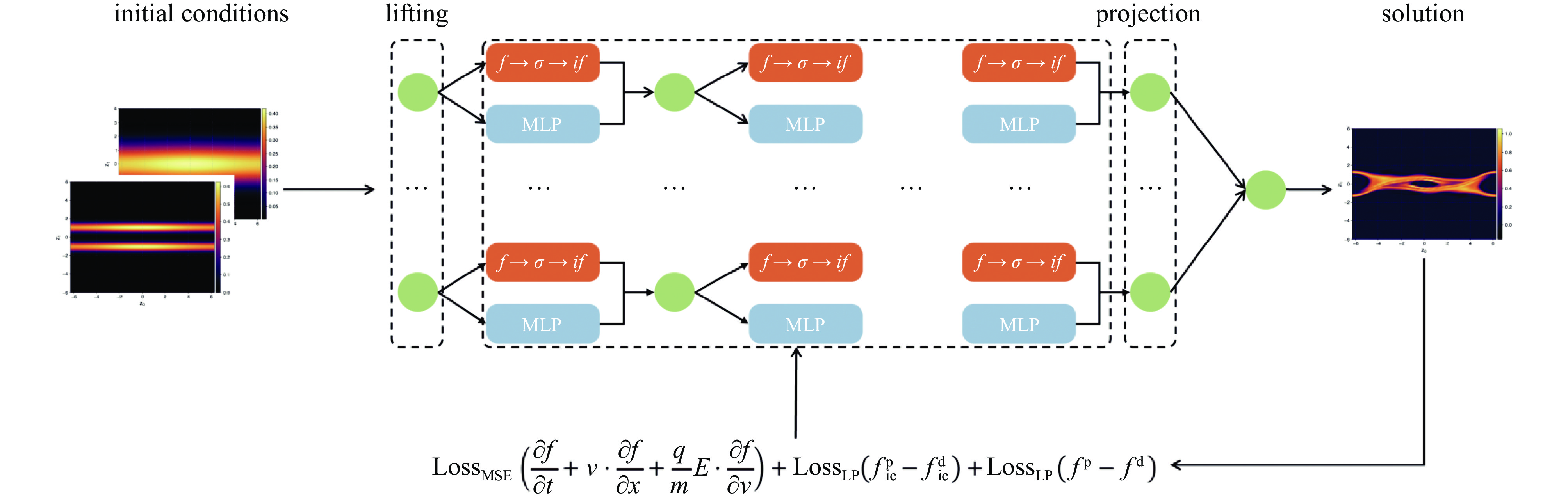
摘要: Vlasov方程是研究等离子体物理的重要方程，在高温、完全电离且忽略库伦碰撞的情况下，其数值求解方法主要有欧拉类方法和拉格朗日类方法。考虑传统数值求解方法在高精度网格条件下计算资源快速增长、维度灾难等问题，采用了基于物理信息驱动的傅里叶神经算子（Physics-informed Fourier Neural Operator, PFNO）对Vlasov方程进行求解。该方法将傅里叶神经算子高维函数映射能力与Vlasov方程物理约束结合，构建了数据-物理信息驱动的深度学习框架，可提升模型在稀疏数据条件下的泛化性能，同时具有网格无关性特征。数值实验表明，该方法在保证求解精度的同时，相比传统有限元法和谱方法计算效率提升1～2个数量级，且能并行处理大批量数据。该研究为高维Vlasov动力学方程的求解提供了新思路，在惯性约束聚变、空间等离子体模拟等领域具有一定应用潜力。Abstract:
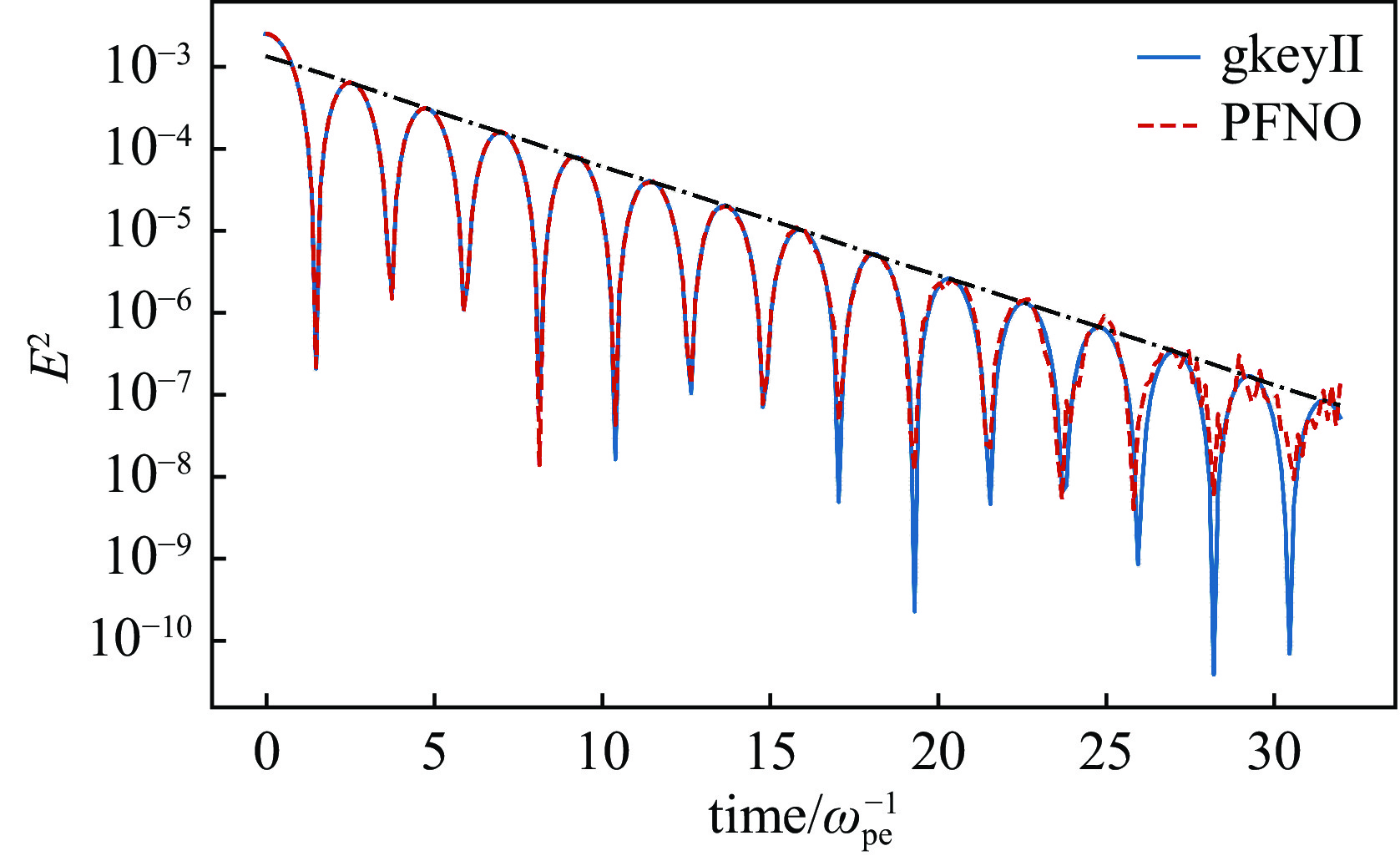
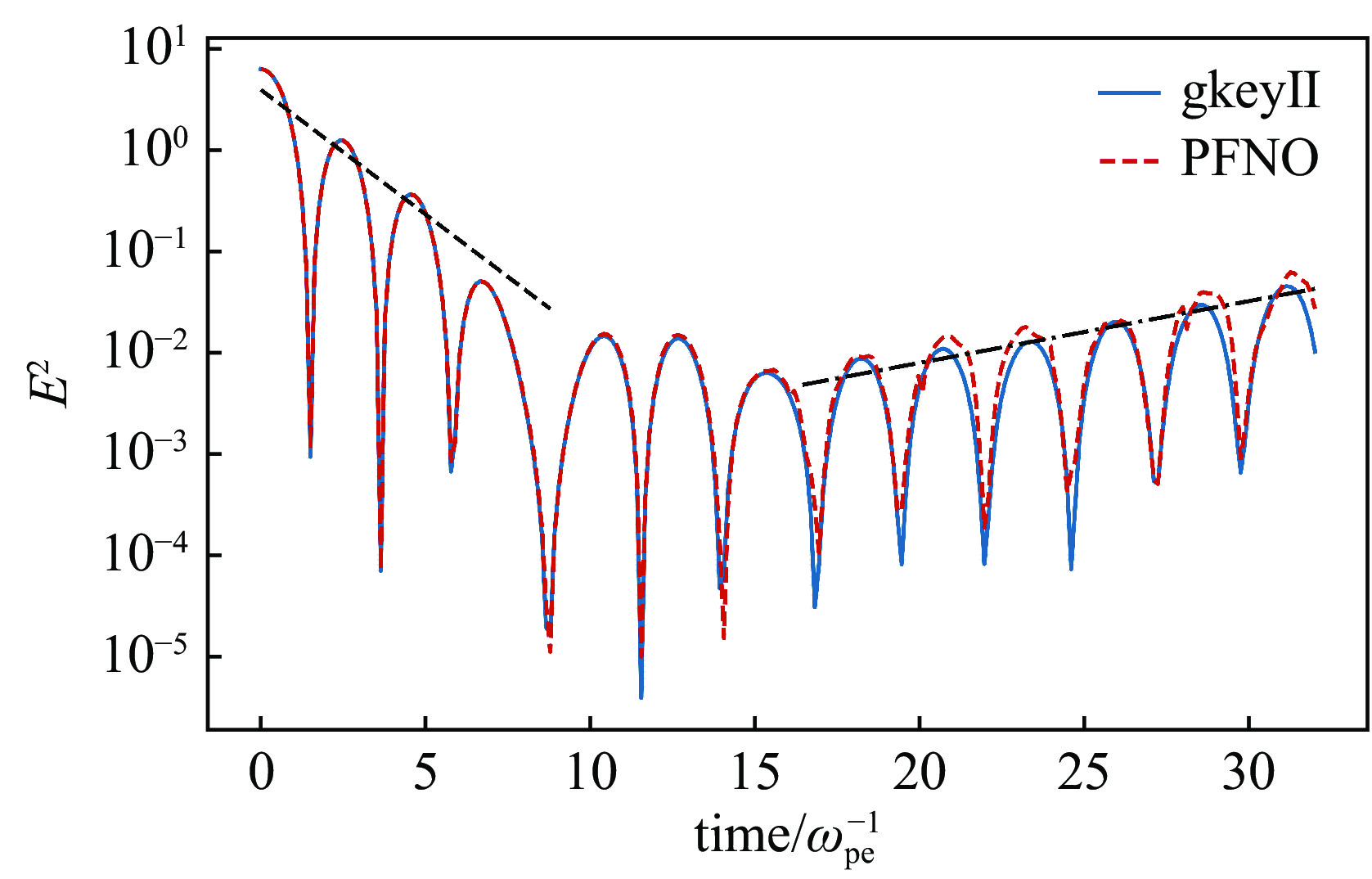
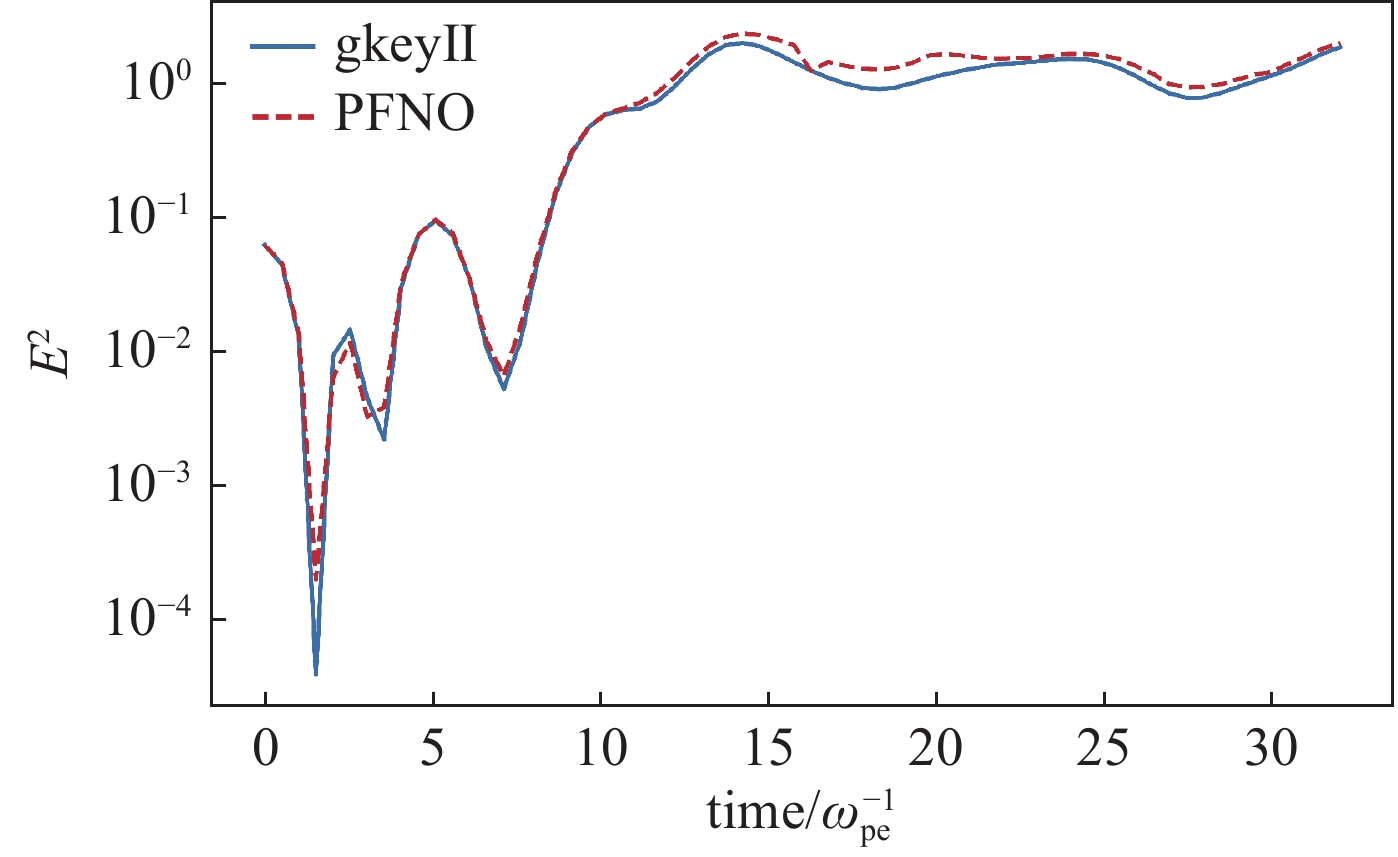
Background The Vlasov equation is a cornerstone in plasma physics, governing the evolution of distribution functions in high-temperature, collisionless plasmas. Conventional numerical methods, including Eulerian and Lagrangian approaches, often encounter severe computational challenges due to the rapid increase in cost with fine grid resolutions and the curse of dimensionality. These limitations restrict their effectiveness in large-scale kinetic plasma simulations needed in fusion research and space plasma studies.Purpose This work aims to develop an efficient and scalable computational framework for solving the Vlasov equation that mitigates the drawbacks of traditional methods. The study particularly addresses the need for maintaining accuracy and physical consistency while significantly reducing computational costs in high-dimensional simulations. An approach based on the Physics-Informed Fourier Neural Operator (PFNO) is introduced.Methods The method integrates the high-dimensional function mapping ability of the Fourier Neural Operator with the physical constraints of the Vlasov equation. A physics-informed loss function is constructed to enforce mass, momentum, and energy conservation laws. The framework was evaluated through benchmark tests against finite element and spectral solvers, and its parallel performance was assessed on large-scale computing platforms.Results The PFNO approach demonstrates accuracy comparable to conventional solvers while achieving computational efficiency improvements of one to two orders of magnitude. The method shows strong generalization under sparse-data conditions, exhibits grid independence, and scales effectively in parallel computing environments, enabling efficient treatment of high-dimensional plasma dynamics. The study presents a novel paradigm for solving high-dimensional Vlasov equations by combining deep learning operators with physical principles.Conclusions The PFNO framework enhances efficiency without sacrificing physical accuracy, making it a promising tool for applications in inertial confinement fusion, astrophysical plasma modeling, and space plasma simulations. Future research directions include extension to multi-species and relativistic plasma systems.-
Key words:
- neural operator /
- Vlasov equation /
- deep learning /
- physics informed /
- plasma
-
图 1 物理信息驱动的傅里叶神经算子网络模型
Figure 1. Physics informed Fourier neural operator network model
图 2 朗道阻尼训练集的损失函数随迭代步的变化
Figure 2. The training loss of the Landau damping dataset as a function of iteration steps
图 3 线性朗道阻尼中的电场能量密度衰减
Figure 3. Decay of the electric field energy density in linear Landau damping
图 4 非线性朗道阻尼中等离子体电场能量密度随时间的演化
Figure 4. The temporal evolution of plasma electric field energy density in nonlinear Landau damping
图 5 双束不稳定性训练集的训练损失随迭代步的变化
Figure 5. The training loss of the two-stream instability dataset as a function of iteration steps
图 7 双束不稳定性中的电场能量密度变化过程
Figure 7. The evolution of electric field energy density in Two-Stream instability
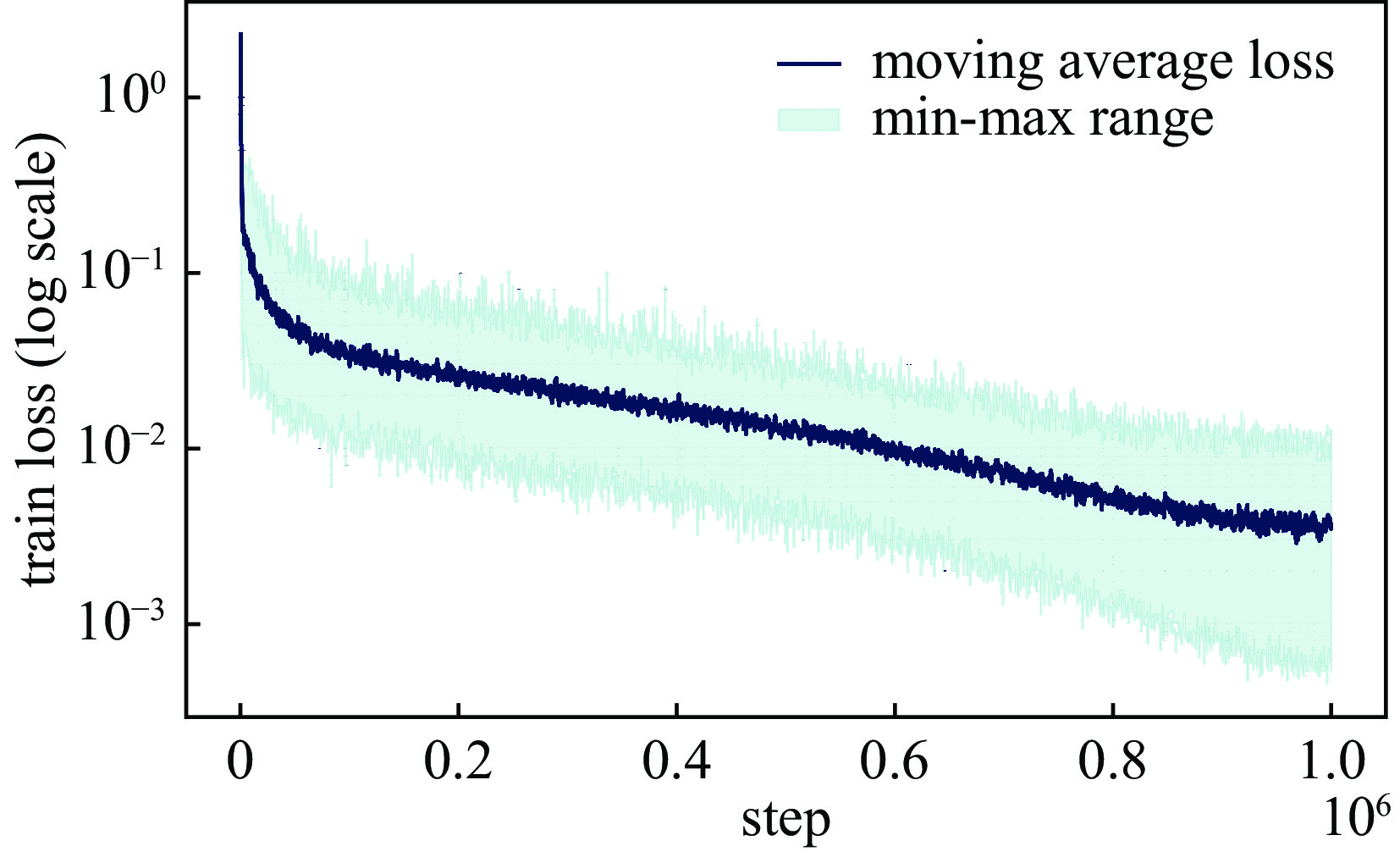
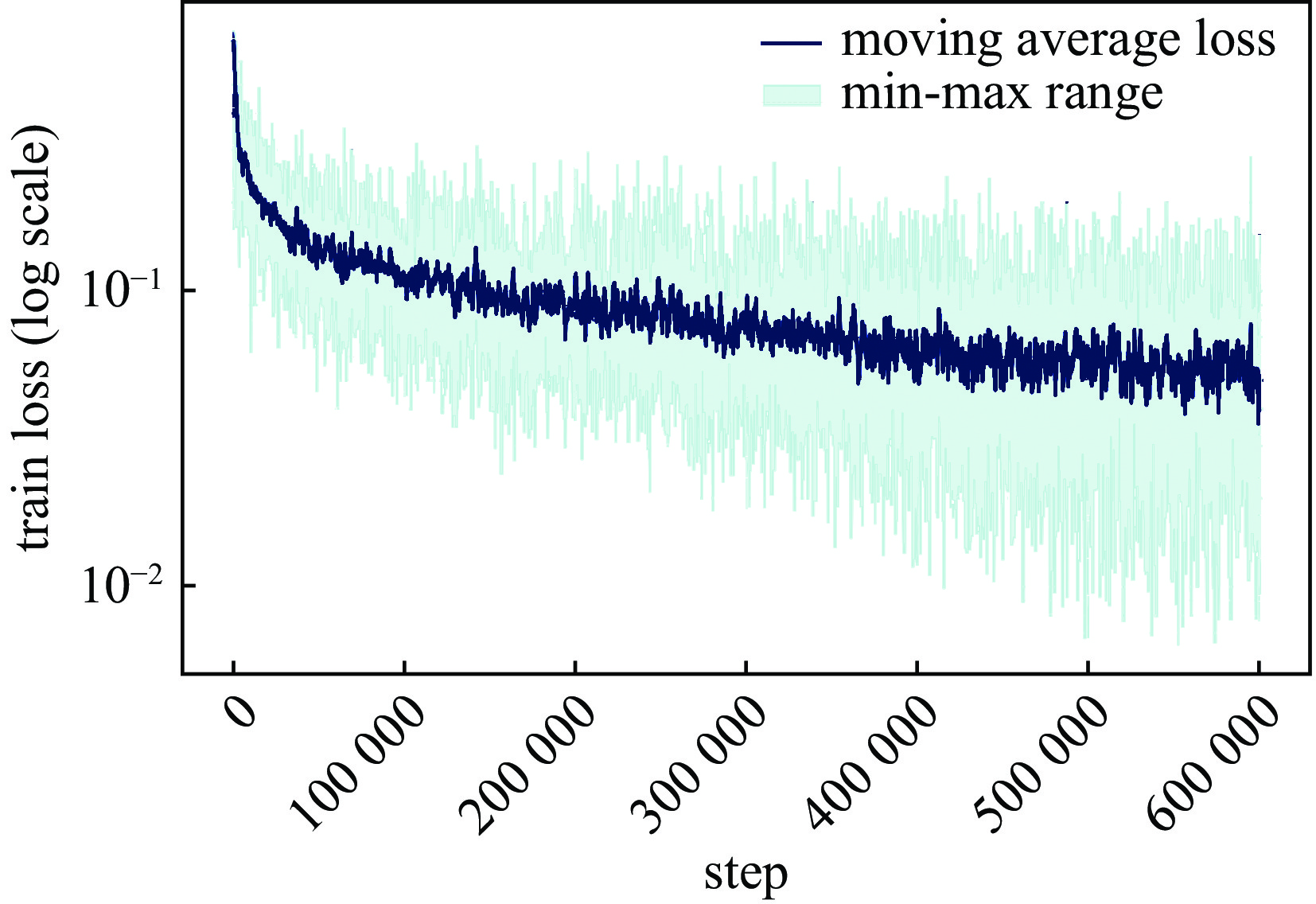
表 1 模型与训练参数
Table 1. Model and training parameters
fully connected layer hidden layers mode number
in x directionmode number
in v directionlearning rate 128 5×32 12 12 0.001 
下载: 导出CSV
表 2 模型与训练参数
Table 2. Model and training parameters
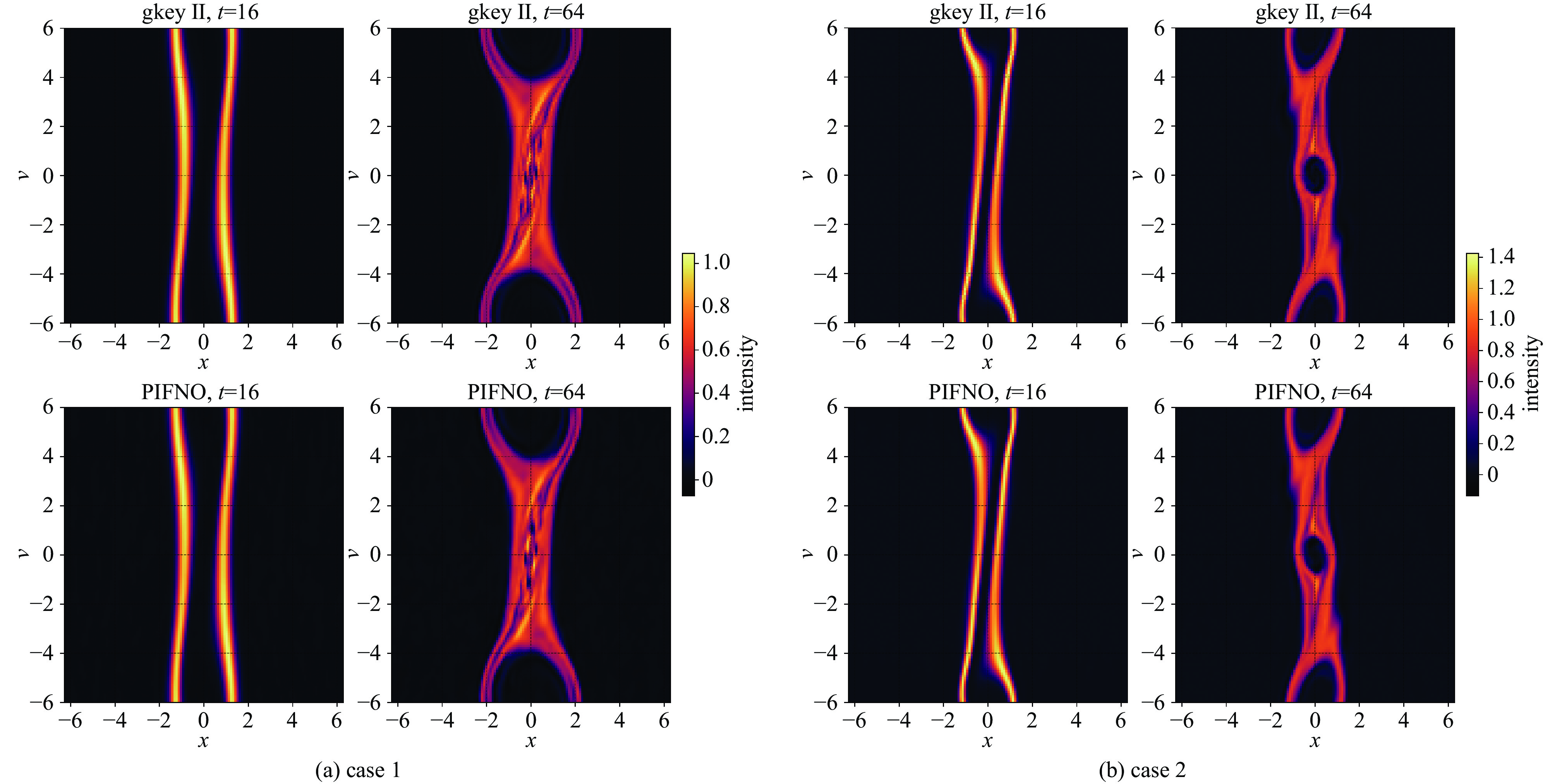
fully connected layer hidden layers mode number in x direction mode number in v direction learning rate 128 5×64 12 12 0.0005
下载: 导出CSV
表 3 PFNO计算精度与耗时对比
Table 3. Comparison of PFNO calculation accuracy and time consumption
resolution number of parameters PFNO L2 error/% time consumption
by Gkey II/stime consumption
by PFNO/sspeed up 128×128 67 M 9.09 450 3.27 137.61 256×256 67 M 8.74 1700 11.24 151.25 128×128 113 M 6.16 450 4.14 108.70 256×256 113 M 6.02 1700 14.63 116.20
下载: 导出CSV
-
[1] Chen, Francis F. Introduction to plasma physics and controlled fusion [M]. Vol. 1. New York: Plenum Press, 1984. [2] Bardos, C, Anne N. A Vlasov equation with Dirac potential used in fusion plasmas [J]. Journal of Mathematical Physics 53, 2012, no. 11. [3] Palmroth, M. , Ganse, U. , et al. Vlasov methods in space physics and astrophysics [J]. Living Reviews in Computational Astrophysics, 2018, 4(1), p. 1. [4] Bertrand P, Albrecht-Marc M, et al. Vlasov models for laser-plasma interaction [J]. Transport Theory and Statistical Physics. 2005 Jan 1;34(1-2): 103-26. [5] Fijalkow, Eric. A numerical solution to the Vlasov equation [J]. Computer Physics Communications, 1999, 116. 2-3: 319-328. [6] Birdsall, C. K, et al. Plasma physics via computer simulation [M]. 2018. [7] Murawski K, Numerical solutions of magnetohydrodynamic equations [J]. Bulletin of the Polish Academy of Sciences-Technical Sciences, 2011, 59(2): 219-226. [8] Sonnendrücker, Eric, et al. The semi-Lagrangian method for the numerical resolution of the Vlasov equation[J]. Journal of Computational Physics, 1999, 149(2): 201-220. doi: 10.1006/jcph.1998.6148 [9] Roska, Tamás, Leon O. Chua, et al. Simulating nonlinear waves and partial differential equations via CNN. I. Basic techniques[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2002(10): 807-815. [10] Kovachki, Nikola, Zongyi Li, et al. Neural operator: learning maps between function spaces with applications to PDES[J]. Journal of Machine Learning Research, 2023, 24(89): 1-97. [11] Raissi, M. , Paris P. , et al. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations [J]. Journal of Computational Physics, 2019, 378 686-707. [12] Zhang, Pan, et al. A Maxwell's equations based deep learning method for time domain electromagnetic simulations[J]. IEEE Journal on Multiscale and Multiphysics Computational Techniques, 2021, 6: 35-40. doi: 10.1109/JMMCT.2021.3057793 [13] Eivazi, Hamidreza, Mojtaba Tahani, et al. Physics-informed neural networks for solving Reynolds-averaged Navier–Stokes equations[J]. Physics of Fluids, 2022(7): 34. [14] Raissi, Maziar. Deep hidden physics models: deep learning of nonlinear partial differential equations[J]. Journal of Machine Learning Research, 2018(25): 1-24. [15] Qin, Yilan, Jiayu Ma, et al. Data-driven modeling of Landau damping by physics-informed neural networks. Physical Review Research, 2023, no. 3: 033079. [16] Juno, James, Ammar Hakim, et al. Discontinuous Galerkin algorithms for fully kinetic plasmas. Journal of Computational Physics 2018, 353: 110-147. -
点击查看大图
计量
- 文章访问数: 10
- HTML全文浏览量: 4
- PDF下载量: 0
- 被引次数: 0
