Numerical simulation study on electromagnetic coupling characteristics of apertures based on FDTD method
-
摘要: 针对电磁脉冲通过孔缝耦合进入电子设备腔体引发的干扰和损坏问题，基于时域有限差分法建立了理想导体矩形腔体的数值模型，系统分析了电磁脉冲的耦合特性。重点考察了不同入射角度和连续脉冲激励下腔体内的电磁场分布规律，采用时频联合分析方法揭示了孔缝耦合的共振机制。结果表明：孔缝耦合会导致特定频率下电场显著增强，其峰值可达入射场的数倍；正入射时腔体内共振效应最为明显，而斜入射条件下不同电场分量因边界条件限制呈现差异化响应；连续脉冲作用会引发电场能量累积，但其增长幅度受腔体驻波效应制约。此外，研究发现腔体共振频率与其结构尺寸密切相关，验证了孔缝耦合的频率选择特性，为电子设备在强电磁环境中的防护设计提供了理论依据和技术参考。Abstract:
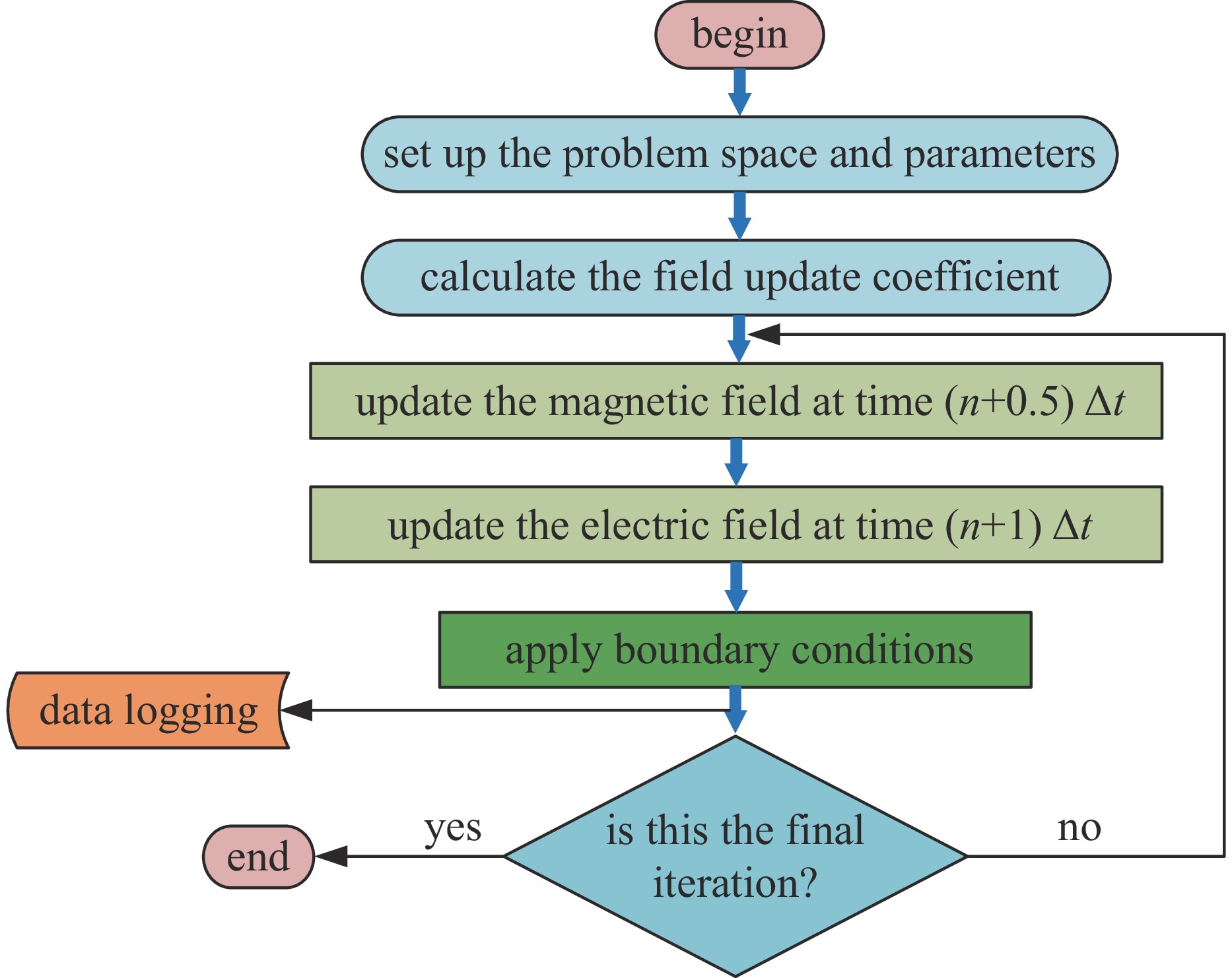
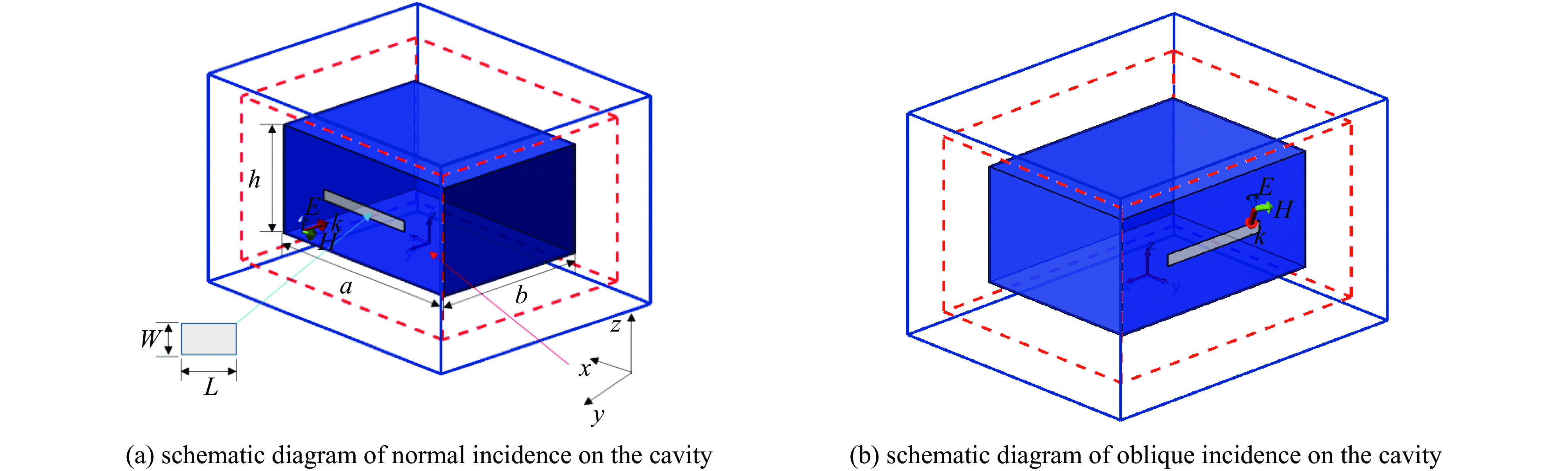
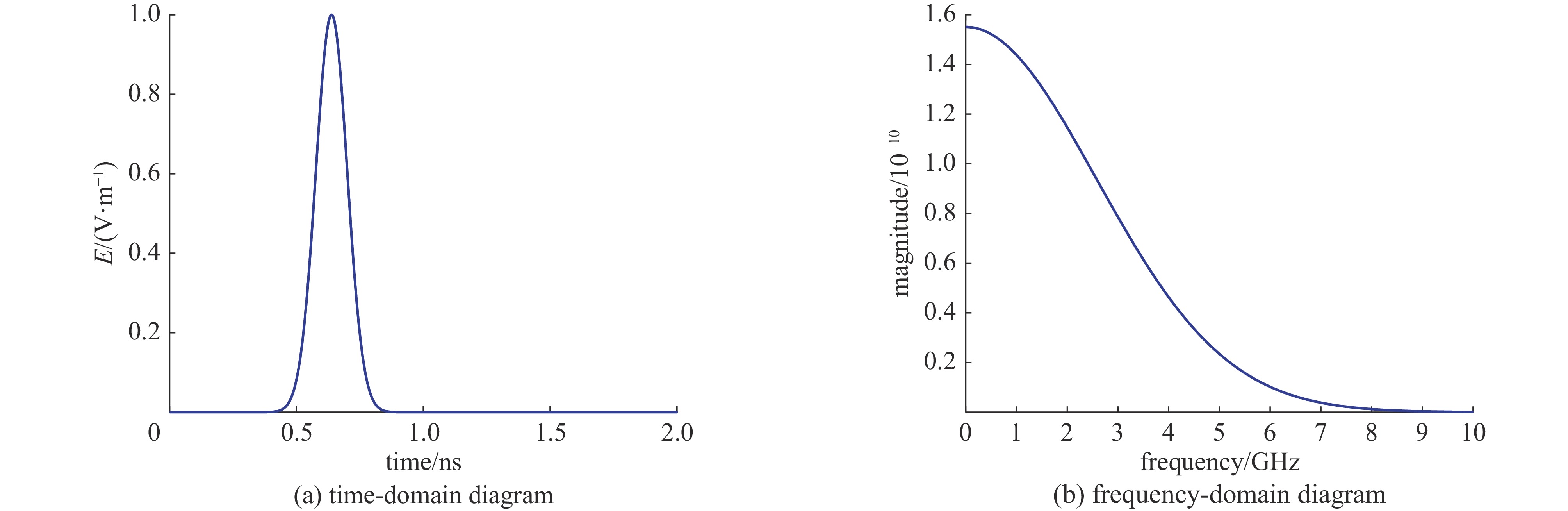
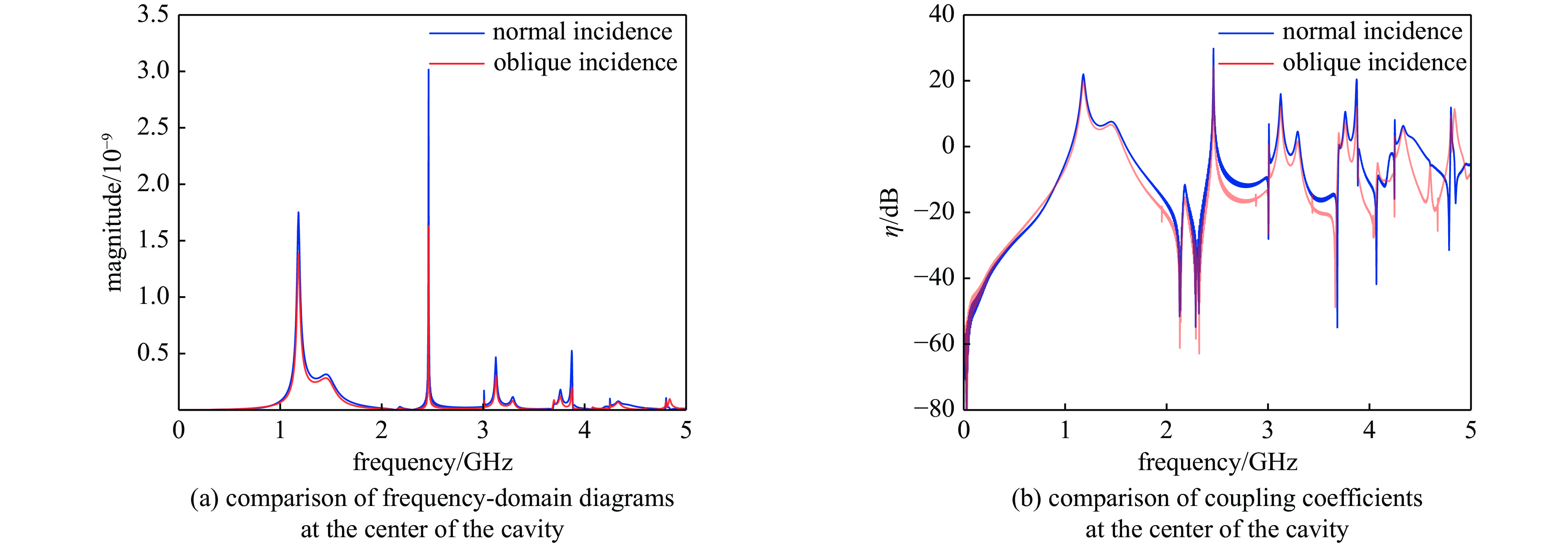
Background Electromagnetic pulses (EMPs) can couple into electronic equipment cavities through apertures, causing severe interference and potential damage. Understanding the coupling characteristics and resonance mechanisms is critical for improving electromagnetic protection design.Purpose This study aims to investigate the coupling effects of EMPs on rectangular cavities with apertures, focusing on field distribution, resonance behavior, and the impact of incidence conditions.Methods A numerical model of a perfectly conducting rectangular cavity was established using the Finite-Difference Time-Domain (FDTD) method. The study analyzed electromagnetic field distributions inside the cavity under varying incidence angles and continuous pulse excitations. A time-frequency joint analysis method was applied to reveal the resonance mechanisms of aperture coupling.Results The results show that aperture coupling produces significant electric field enhancement at specific frequencies, with peak amplitudes several times larger than the incident field. Normal incidence yields the strongest resonant effects, while oblique incidence leads to different responses in electric field components due to boundary constraints. Continuous pulse excitation results in electric field energy accumulation, though limited by standing-wave effects. The resonant frequencies were found to be strongly dependent on cavity dimensions, confirming the frequency-selective characteristics of aperture coupling.Conclusions This research establishes the theoretical basis for understanding EMP aperture coupling and provides technical references for designing protection measures in high-intensity electromagnetic environments.-
Key words:
- FDTD /
- electromagnetic pulse /
- aperture coupling /
- resonance effect /
- incidence angle
-
图 3 电磁脉冲入射腔体示意图
Figure 3. Schematic diagram of electromagnetic pulse incident on a cavity
图 6 狭缝中心与腔体中心功率密度
Figure 6. Power density at the center of the slit and the center of the cavity
图 7 狭缝中心与腔体中心频域图
Figure 7. Frequency domain diagram at the center of the slit and the center of the cavity
图 8 腔体中心与狭缝中心取样电场时域图
Figure 8. Time domain diagram of the sampled electric field at the center of the cavity and the center of the slit
图 9 腔体中心电场频域图
Figure 9. Frequency domain diagram of the electric field at the center of the cavity
图 10 平面波正入射和斜入射腔体中心频域图和耦合系数
Figure 10. Frequency domain diagram and coupling coefficient at the center of the cavity under normal and oblique incidence of plane waves
图 12 不同数量脉冲群激励下腔体中心时域图
Figure 12. Time domain diagram at the center of the cavity under excitation by pulse groups of different quantities
图 13 不同间隔脉冲群激励下腔体中心时域图
Figure 13. Time domain diagram at the center of the cavity under excitation by pulse groups with different intervals
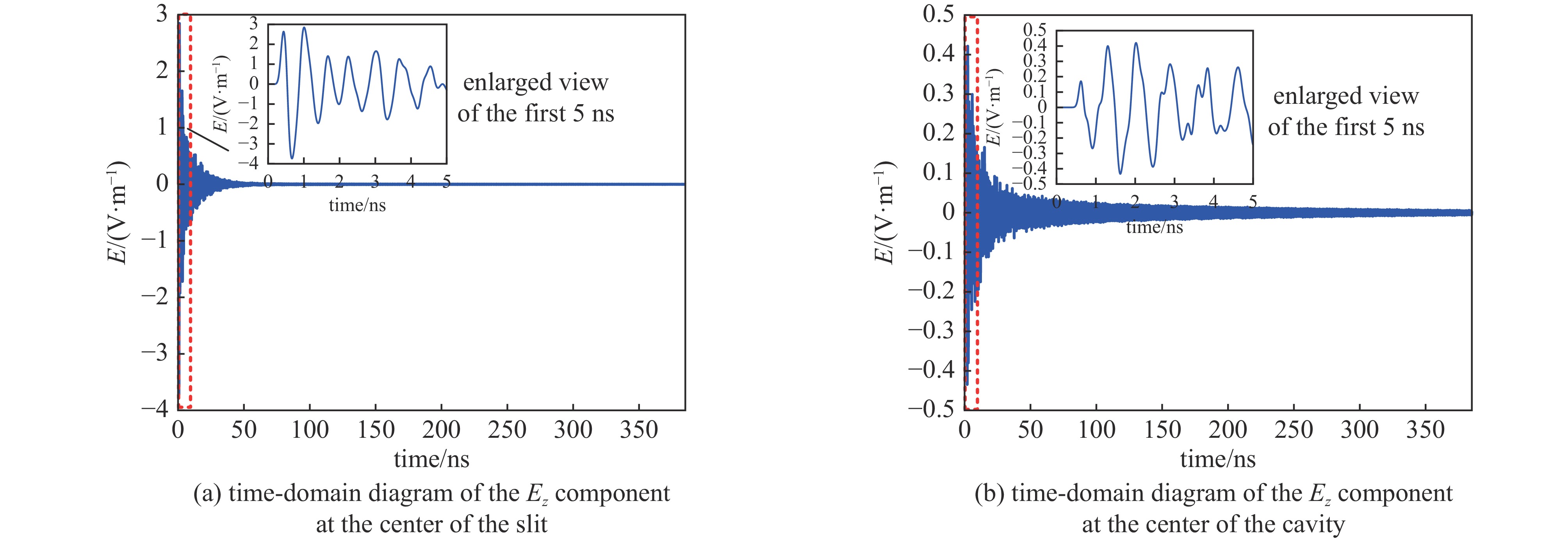
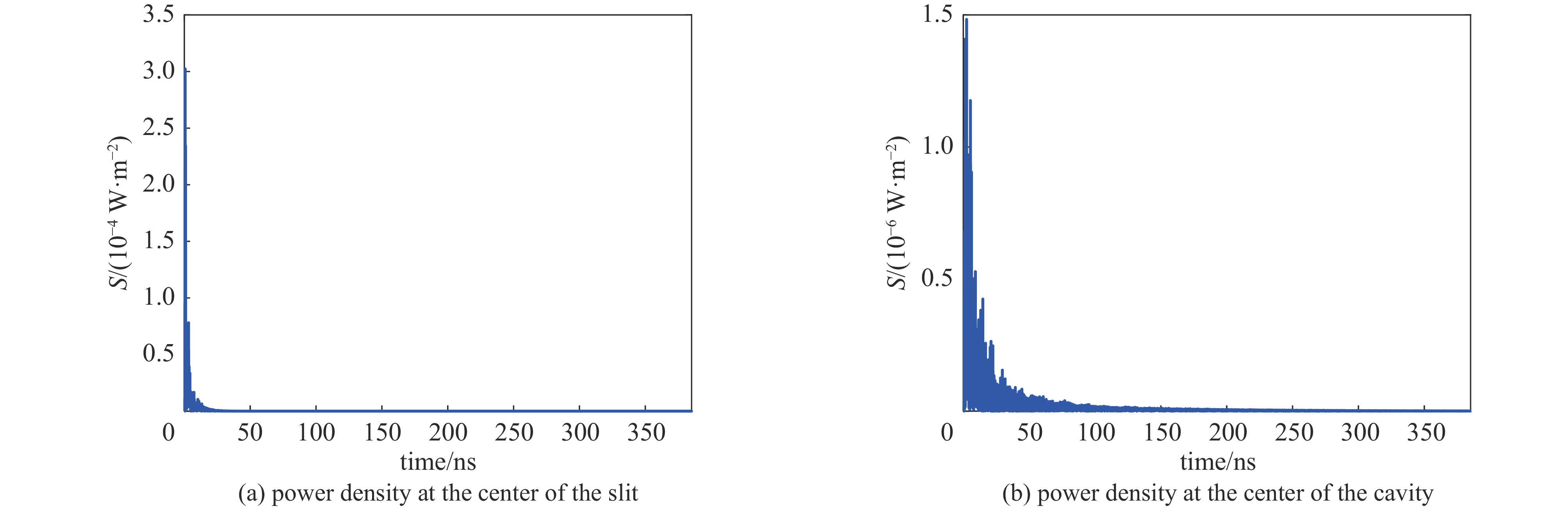
表 1 不同时间段电场与功率密度峰值
Table 1. Peak values of electric field and power density at different time periods
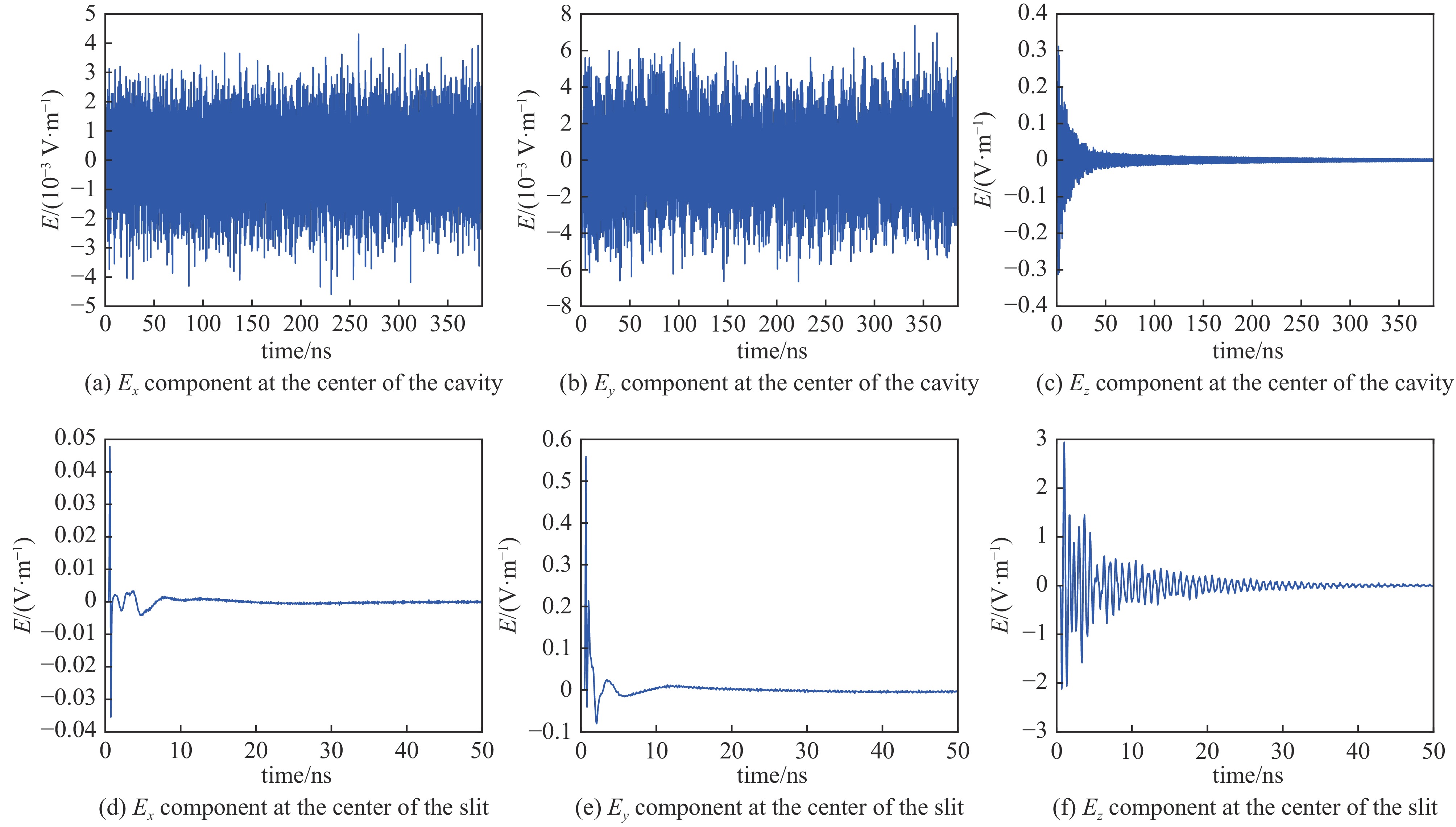
time period/ns peak value of the electric field Ez component/(V·m−1) peak value of power density/(W·m−2) center of the slit center of the cavity center of the slit center of the cavity 0～50 3.7375 0.4344 3.0241 ×10−41.4830 ×10−650～100 0.0260 0.0429 5.0991 ×10−85.8427 ×10−8100～150 0.0082 0.0246 7.9147 ×10−91.8574 ×10−8150～200 0.0063 0.0181 3.4811 ×10−91.0960 ×10−8200～250 0.0050 0.0144 2.1121 ×10−96.1948 ×10−9250～300 0.0039 0.0112 1.5757 ×10−93.8135 ×10−9300～350 0.0031 0.0090 1.0266 ×10−92.2787 ×10−9
下载: 导出CSV
表 2 腔体中心与狭缝中心时域图峰值
Table 2. Peak values of time domain diagrams at the center of the cavity and the center of the slit
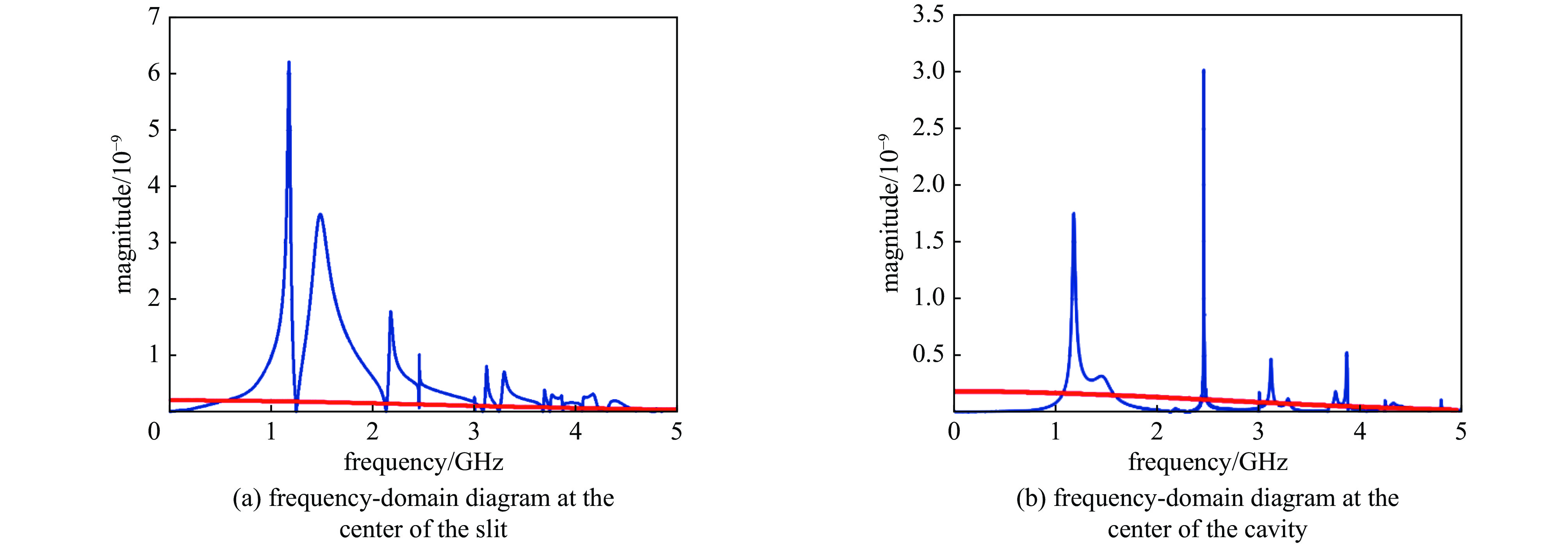
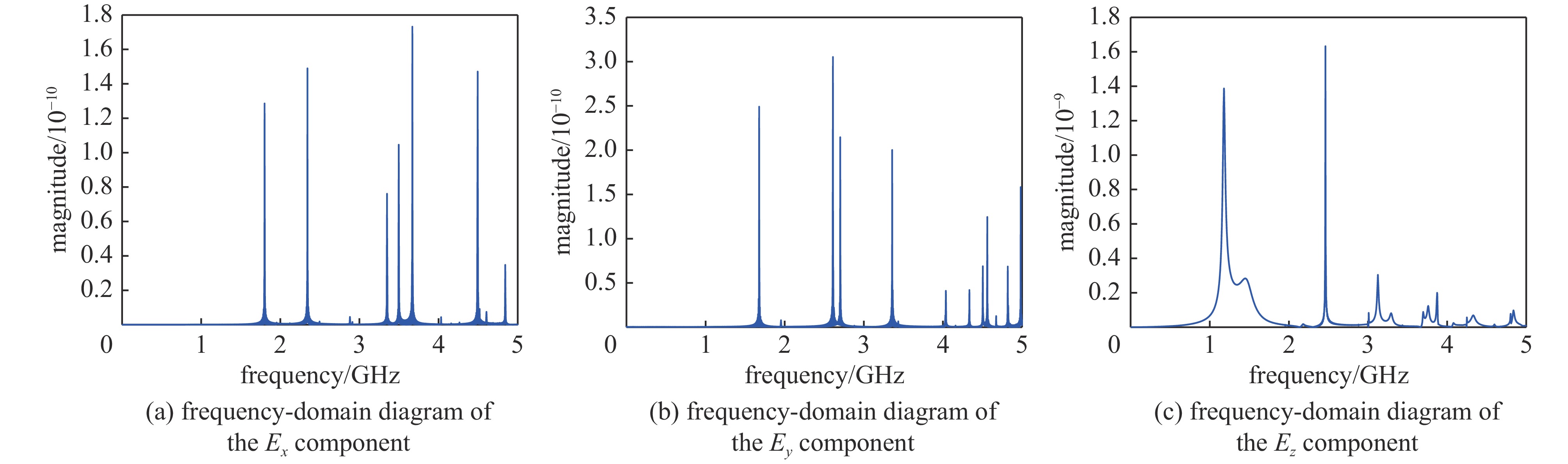
sampling point Ex/(V·m−1) Ey/(V·m−1) Ez/(V·m−1) center of the slit 0.0478 0.5585 2.9415 center of the cavity 0.0043 0.0074 0.3114
下载: 导出CSV
表 3 腔体中心电场第一个共振峰频率与谐振腔低次模频率
Table 3. First resonance peak frequency of the electric field at the center of the cavity and the lower mode frequencies of the resonant cavity
Ex/TE011/GHz) Ey/TE101/GHz) Ez/TE110/GHz) first resonance peak frequency 1.8010 1.6771 1.1793 resonant frequency of the cavity 1.8028 1.6771 1.2500
下载: 导出CSV
表 4 不同数量脉冲激励下腔体中心电场峰值
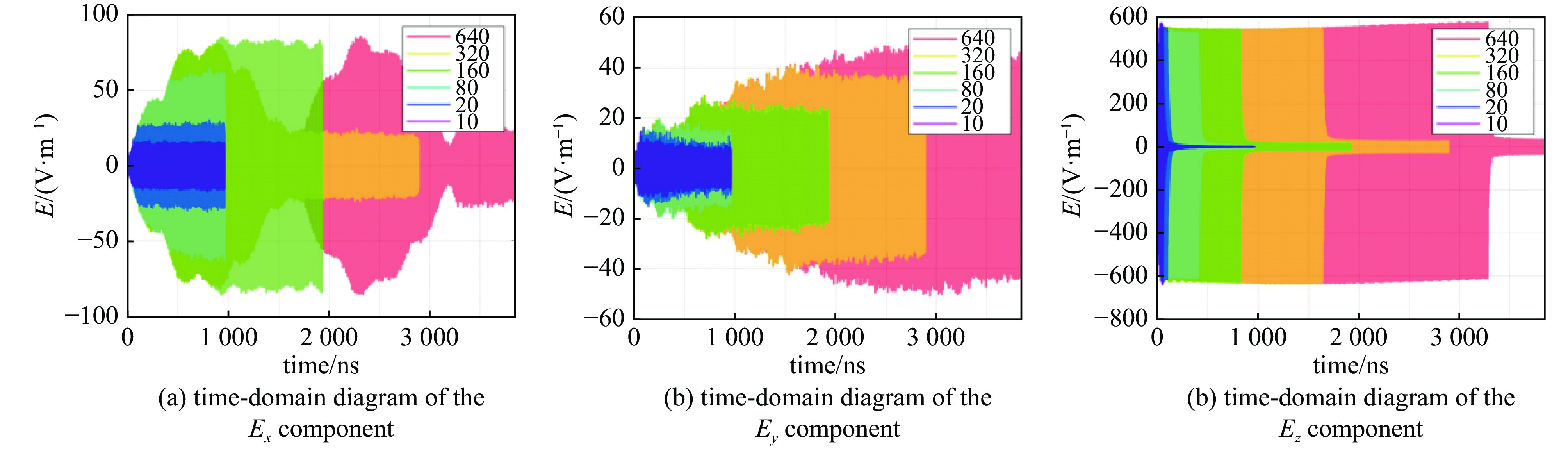
Table 4. Peak values of the electric field at the center of the cavity under excitation by different numbers of pulses
number of incident
pulsespulse
duration/nspeak value of
Ex/(V·m−1)peak value of
Ey/(V·m−1)peak value of
Ez/(V·m−1)peak value of power
density/(W·m−2)10 51 16.1543 14.1553 573.4260 72.6571 20 102 30.3846 15.9893 573.4340 72.6292 80 410 65.0853 19.7964 561.0220 68.3825 160 820 84.8765 28.9687 573.4880 72.6366 320 1639 80.9581 41.0330 573.4640 72.7335 640 3279 85.4996 52.3679 576.6630 72.6639
下载: 导出CSV
表 5 不同间隔脉冲群激励下腔体中心电场峰值
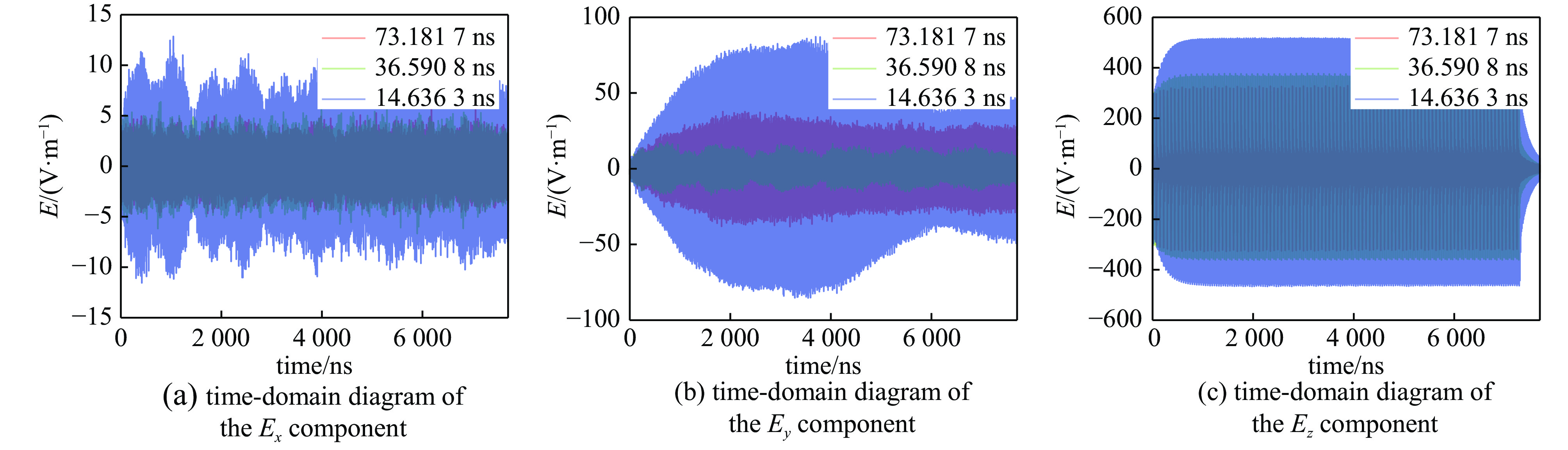
Table 5. Peak values of the electric field at the center of the cavity under excitation by pulse groups with different intervals
pulse
interval/nspulse
duration/nspeak value of
Ex/(V·m−1)peak value of
Ey/(V·m−1)peak value of
Ez/(V·m−1)peak value of power
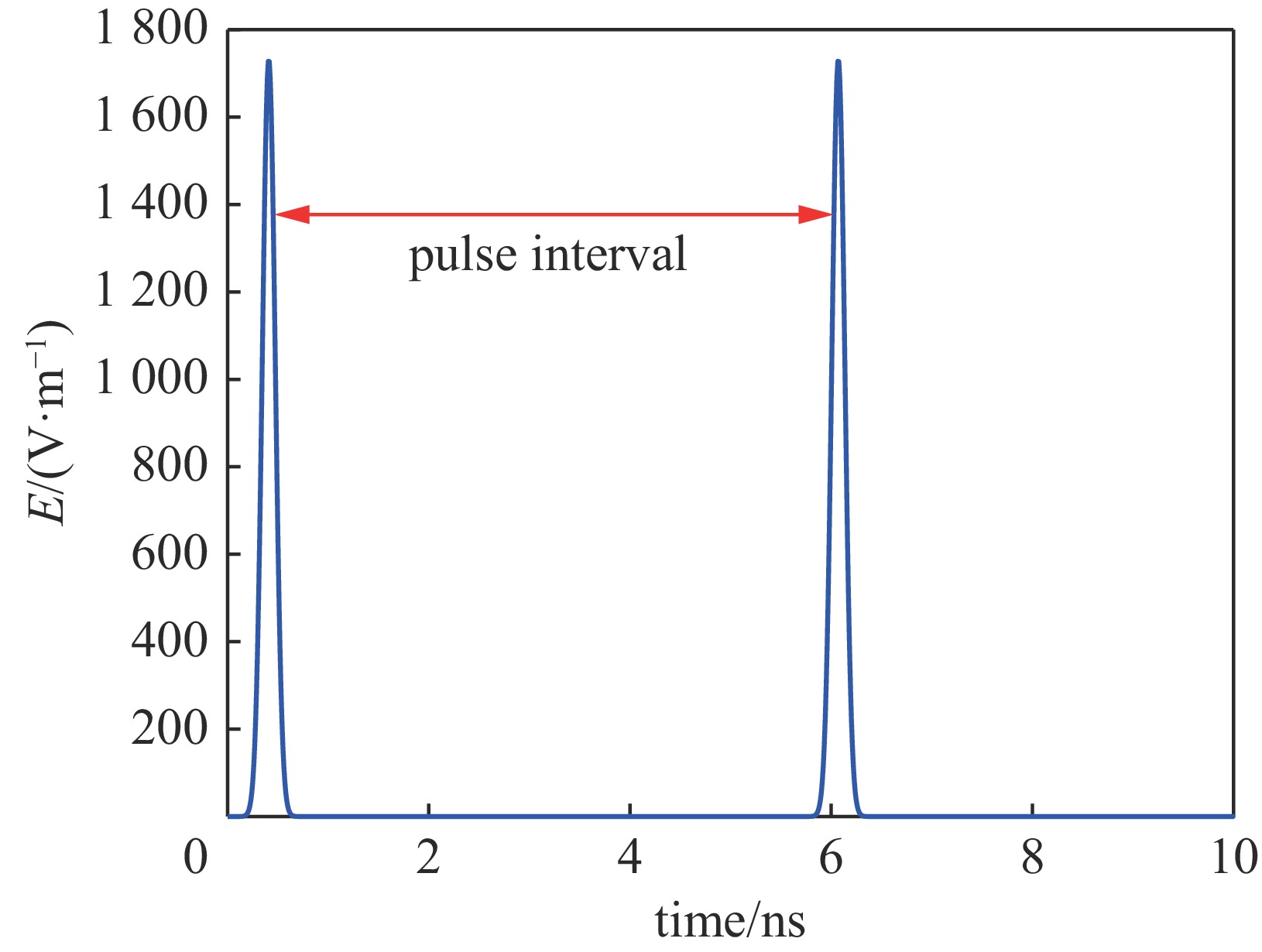
density/(W·m−2)14.6363 7318 12.8499 87.0833 518.7520 85.3471 36.5908 7318 6.3700 17.4389 377.0730 34.8544 73.1817 7318 5.6504 37.6508 331.4450 33.2875
下载: 导出CSV
-
[1] 冯溪溪, 赵景涛, 曹垒. 典型后门耦合目标回波信号特性分析[J]. 强激光与粒子束, 2024, 36: 043008 doi: 10.11884/HPLPB202436.230272Feng Xixi, Zhao Jingtao, Cao Lei. Characteristic analysis of echo signal of typical backdoor coupling target[J]. High Power Laser and Particle Beams, 2024, 36: 043008 doi: 10.11884/HPLPB202436.230272 [2] IEC 61000-4-21, Electromagnetic compatibility (EMC) - Part 4-21: testing and measurement techniques - Reverberation chamber test methods[S]. [3] GJB 8810-2015, 小屏蔽体屏蔽效能测量方法[S]. [4] Bethe H A. Theory of diffraction by small holes[J]. Physical Review, 1944, 66(7/8): 163-182. [5] Solin J R. Formula for the field excited in a rectangular cavity with an aperture and lossy walls[J]. IEEE Transactions on Electromagnetic Compatibility, 2015, 57(2): 203-209. doi: 10.1109/TEMC.2014.2368124 [6] 张亚普, 达新宇, 祝杨坤, 等. 电大开孔箱体屏蔽效能分析解析模型[J]. 物理学报, 2014, 63: 234101 doi: 10.7498/aps.63.234101Zhang Yapu, Da Xinyu, Zhu Yangkun, et al. Formulation for shielding effectiveness analysis of a rectangular enclosure with an electrically large aperture[J]. Acta Physica Sinica, 2014, 63: 234101 doi: 10.7498/aps.63.234101 [7] Robinson M P, Benson T M, Christopoulos C, et al. Analytical formulation for the shielding effectiveness of enclosures with apertures[J]. IEEE Transactions on Electromagnetic Compatibility, 1998, 40(3): 240-248. doi: 10.1109/15.709422 [8] Po'ad F A, Jenu M Z M, Christopoulos C, et al. Analytical and experimental study of the shielding effectiveness of a metallic enclosure with off-centered apertures[C]//Proceedings of the 17th International Zurich Symposium on Electromagnetic Compatibility. 2006. [9] Shi Dan, Lv Na, Gao Yougang. Shielding effectiveness estimation of a metallic enclosure with an off-center aperture for obliquely incident & arbitrary polarized plane wave[J]. ACES Journal, 2017, 32(4): 352-357. [10] Ren Dan, Du Ping’an, He Yin, et al. A fast calculation approach for the shielding effectiveness of an enclosure with numerous small apertures[J]. IEEE Transactions on Electromagnetic Compatibility, 2016, 58(4): 1033-1041. doi: 10.1109/TEMC.2016.2547739 [11] 王建国, 刘国治, 周金山. 微波孔缝线性耦合函数研究[J]. 强激光与粒子束, 2003, 15(11): 1093-1099Wang Jianguo, Liu Guozhi, Zhou Jinshan. Investigations on function for linear coupling of microwaves into slots[J]. High Power Laser and Particle Beams, 2003, 15(11): 1093-1099 [12] Chen Juan, Wang Jianguo. A three-dimensional HIE-PSTD scheme for simulation of thin slots[J]. IEEE Transactions on Electromagnetic Compatibility, 2013, 55(6): 1239-1249. doi: 10.1109/TEMC.2013.2265037 [13] 倪勤, 魏志勇, 强鹏, 等. 电磁脉冲与腔体孔缝耦合多峰共振特性研究[J]. 核电子学与探测技术, 2014, 34(7): 855-860,865 doi: 10.3969/j.issn.0258-0934.2014.07.012Ni Qin, Wei Zhiyong, Qiang Peng, et al. Investigation on multi- peak resonant electromagnetic pulse coupling into the cavity with a narrow slot[J]. Nuclear Electronics & Detection Technology, 2014, 34(7): 855-860,865 doi: 10.3969/j.issn.0258-0934.2014.07.012 [14] 李智慧, 唐靖宇, 张伦. 有限积分理论(FIT)及其在腔体计算中的应用[J]. 强激光与粒子束, 2002, 14(1): 156-160Li Zhihui, Tang Jingyu, Zhang Lun. Finite integral theory and its application on cavity simulation[J]. High Power Laser and Particle Beams, 2002, 14(1): 156-160 [15] 吴刚, 张新刚, 刘波. 有孔矩形金属腔体屏蔽效能的估算[J]. 强激光与粒子束, 2011, 23(3): 743-748 doi: 10.3788/HPLPB20112303.0743Wu Gang, Zhang Xingang, Liu Bo. Prediction for shielding effectiveness of rectangular metallic enclosure with aperture[J]. High Power Laser and Particle Beams, 2011, 23(3): 743-748 doi: 10.3788/HPLPB20112303.0743 [16] 安静, 武俊峰, 吴一辉. 孔缝对内置电路板壳体屏蔽效能的影响[J]. 微波学报, 2011, 27(2): 34-37An Jing, Wu Junfeng, Wu Yihui. Influence of apertures on shielding effectiveness for shell of loaded PCB[J]. Journal of Microwaves, 2011, 27(2): 34-37 [17] Araneo R, Lovat G. Analysis of the shielding effectiveness of metallic enclosures excited by internal sources through an efficient method of moment approach[J]. ACES Journal, 2010, 25(7): 600-611. [18] Schröder A, Rasek G A, Brüns H D, et al. Analysis of high intensity radiated field coupling into aircraft using the method of moments[J]. IEEE Transactions on Electromagnetic Compatibility, 2014, 56(1): 113-122. doi: 10.1109/TEMC.2013.2278208 [19] 肖金石, 刘文化, 张世英, 等. 超宽带电磁脉冲对腔体孔缝耦合效应的数值模拟[J]. 强激光与粒子束, 2010, 22(12): 2959-2963 doi: 10.3788/HPLPB20102212.2959Xiao Jinshi, Liu Wenhua, Zhang Shiying, et al. Numerical simulation on coupling effects of ultra wide band electromagnetic pulse into slots in a cavity[J]. High Power Laser and Particle Beams, 2010, 22(12): 2959-2963 doi: 10.3788/HPLPB20102212.2959 -
点击查看大图
计量
- 文章访问数: 8
- HTML全文浏览量: 2
- PDF下载量: 0
- 被引次数: 0
