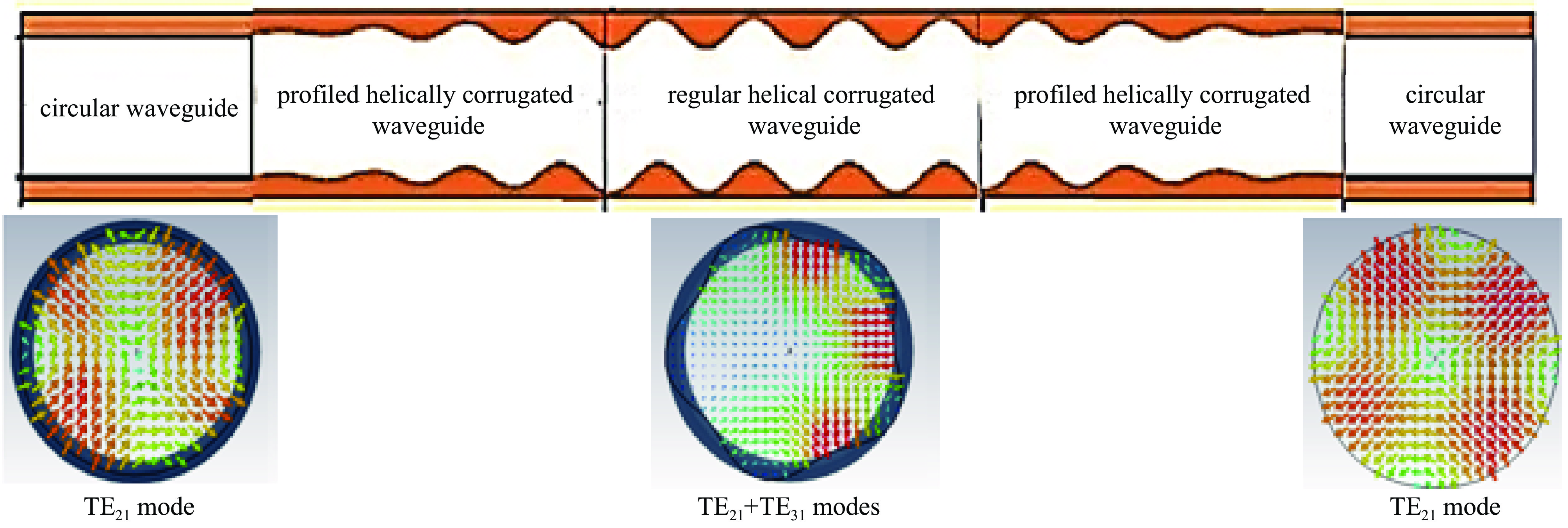
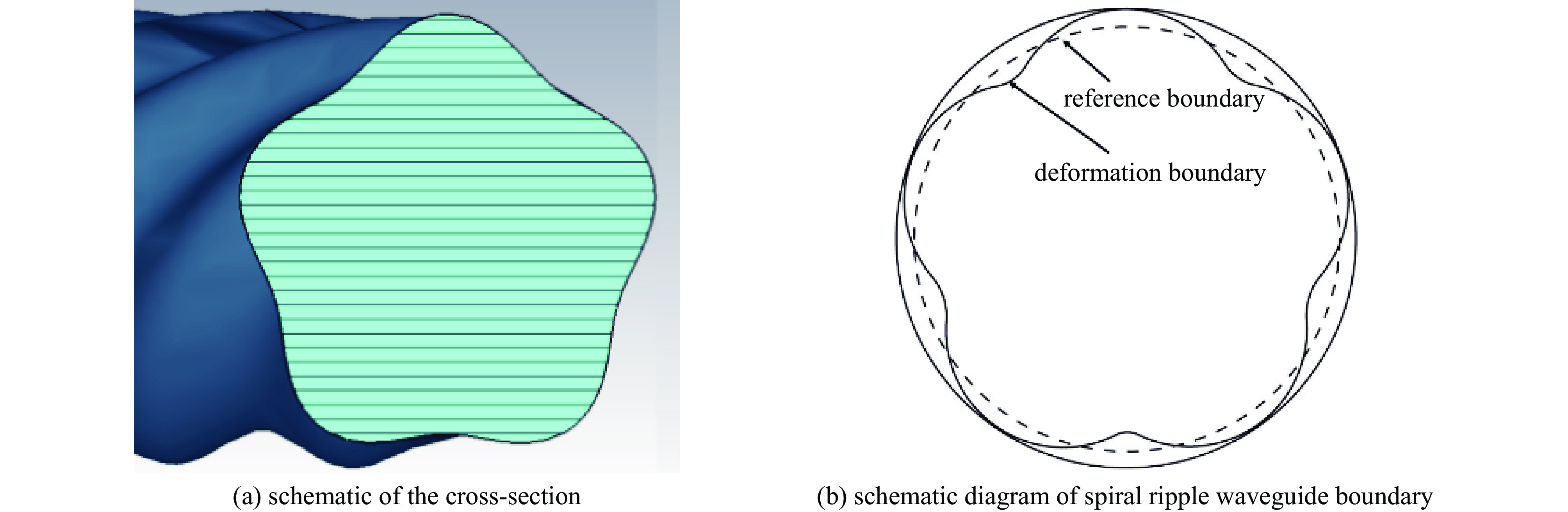
Study on the dispersion characteristics of a five-fold helical corrugated waveguide
-
摘要: 回旋行波管在毫米波雷达、通信、电子对抗、深空探测等方面有重要应用。对于大回旋状态下的电子注，只与
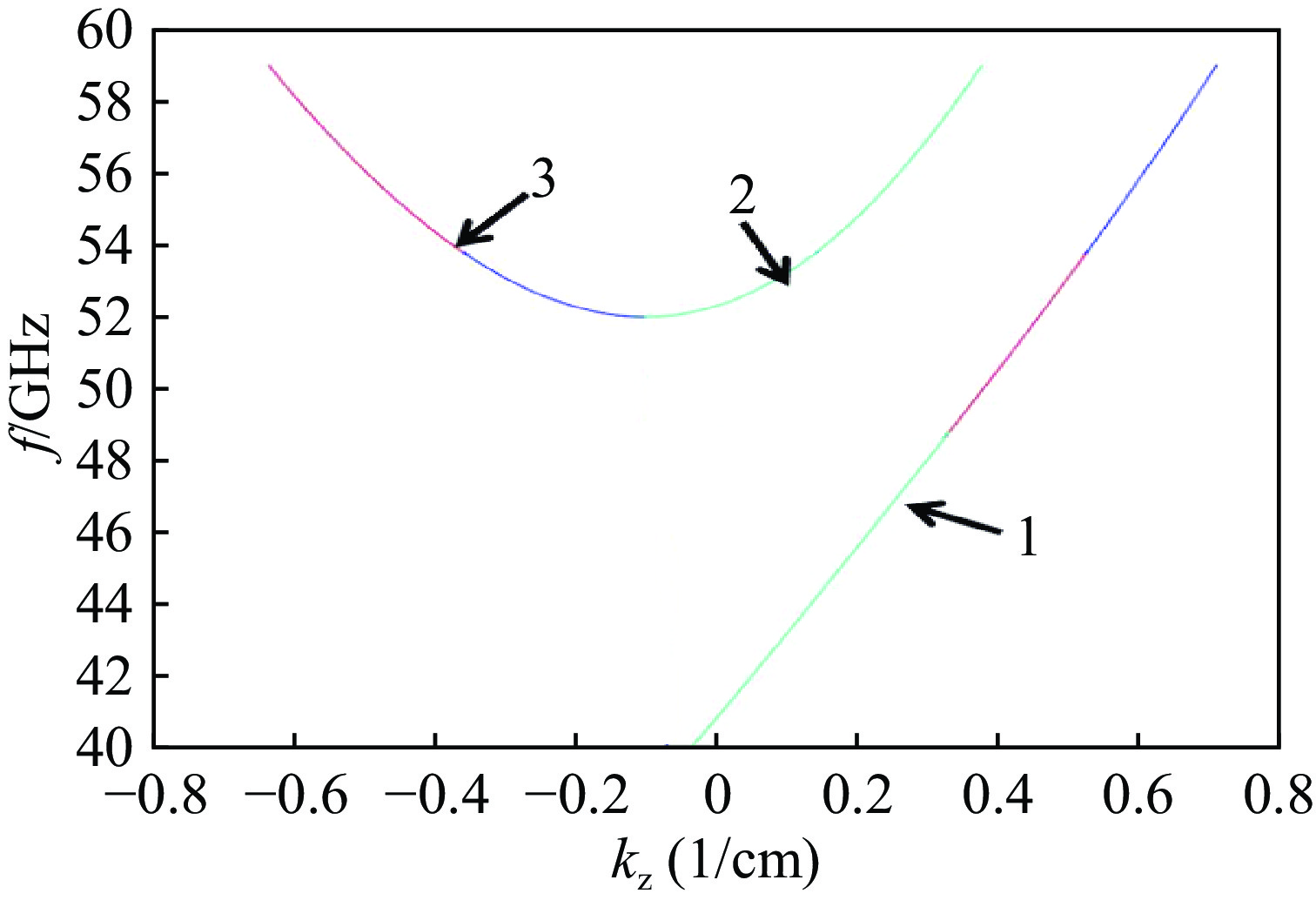
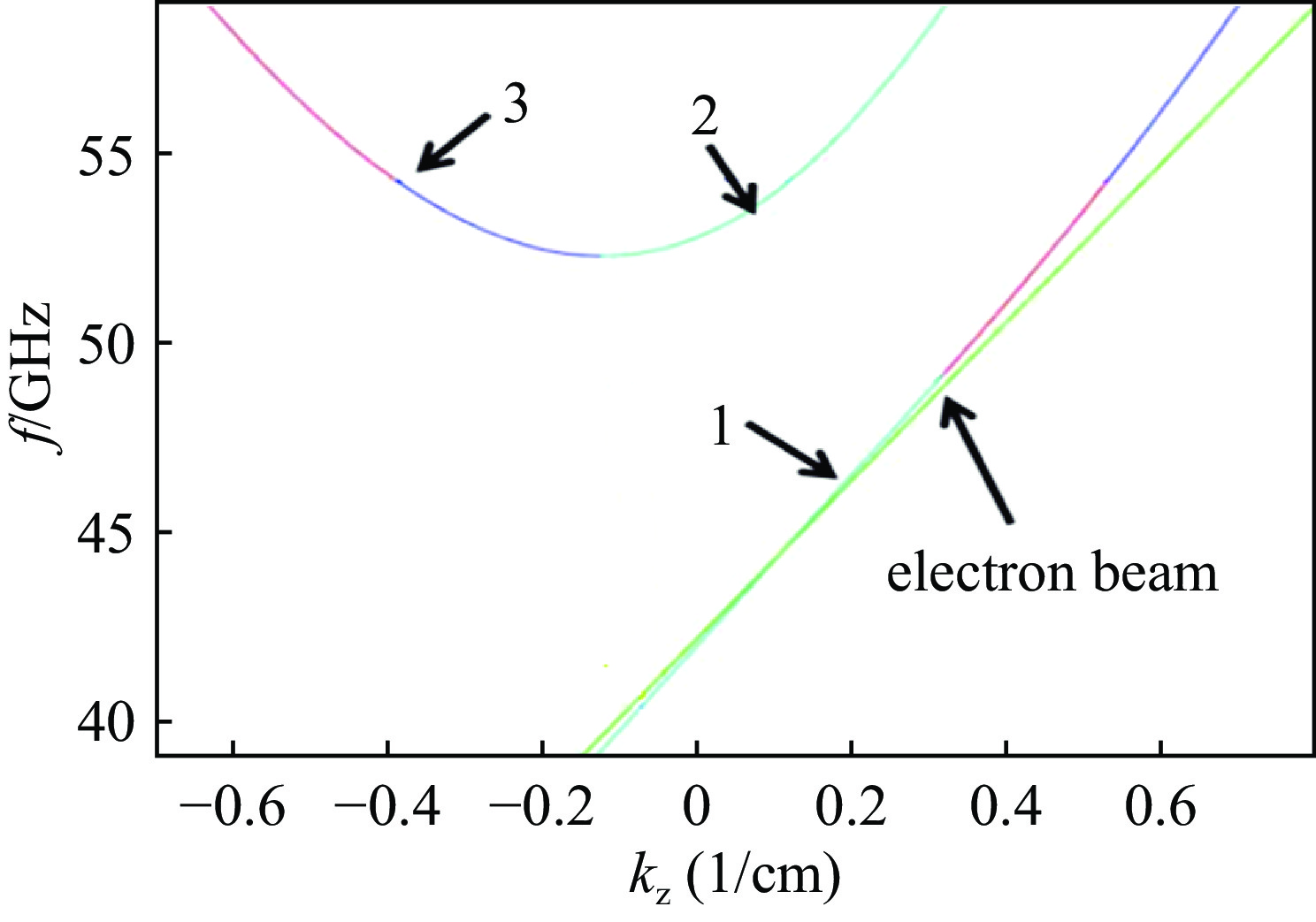
$ \mathit{s}=\mathit{m} $ 的模式相互作用，其中，s为谐波次数，m为模式的角向指标，利于模式竞争的抑制。为了研究螺纹起伏参数和螺纹周期的改变对于工作模式1曲线的影响，本文利用阻抗微绕法，通过波耦合方程，得到五折叠Q波段螺旋波纹波导的传输耦合方程，分析了五折叠Q波段螺旋波纹波导模式耦合规则，并给出其色散方程，对色散方程进行数值求解，得到五折叠Q波段螺旋波纹波导的色散曲线，通过分析色散特性可知，在波导中有3个本征模式，模式1和2、3模基本完全分离，选取模式1为工作模式，在42～47 GHz的范围内和电子注模式可以在较宽的范围内相切，不仅极大地拓展了互作用带宽，还可抑制模式竞争。Abstract: Gyrotron traveling wave tube (gyro-TWT) hold significant applications in millimeter-wave radar, communications, electronic warfare, and deep-space exploration. For electron beams operating in the large-orbit regime, interaction occurs exclusively with modes satisfying$ s=m $ , where s denotes the harmonic number and m represents the azimuthal index of the mode. This selective interaction favors the suppression of mode competition. To investigate the effects of variations in thread fluctuation parameters and thread period on the dispersion characteristics of operating mode 1, this study investigates the dispersion characteristics of a five-fold helical corrugated waveguide operating in the Q-band using the impedance perturbation technique combined with wave coupling theory. The transmission coupling equations are derived, and the mode coupling behavior within the waveguide is systematically characterized. Based on the established coupling model, the dispersion equation is formulated and subsequently solved through numerical methods to obtain the dispersion curves. The analysis reveals the presence of three intrinsic eigenmodes, among which Mode 1 exhibits strong isolation from Modes 2 and 3. Mode 1 is therefore selected as the primary operating mode. Within the 42–47 GHz frequency range, favorable phase synchronism is achieved between Mode 1 and the large-orbit electron beam, enabling broadband beam–wave interaction. This configuration not only substantially enhances the interaction bandwidth but also provides effective suppression of mode competition. -
图 1 五折叠螺旋波纹波导截面示意图及螺旋波纹波导边界示意图
Figure 1. Schematic of the cross-section of a five-folded spiral corrugated waveguide and schematic diagram of spiral ripple waveguide boundary
图 2 五折叠螺旋波纹波导高频结构示意图及场分布图
Figure 2. Schematic diagram and field distribution of high-frequency structure of five-folded spiral corrugated waveguide
图 3 Q波段五折叠螺旋波纹波导色散曲线图
Figure 3. Dispersion diagram of Q-band spiral ripple waveguide gyratory traveling wave tube
图 4 Q波段五折叠螺旋波纹波导色散曲线图与电子注回旋模式图
Figure 4. Dispersion diagram of Q-band spiral ripple waveguide gyratory traveling wave tube
表 1 螺旋波纹波导模式耦合结果
Table 1. Coupling results of spiral ripple waveguide modes
Coupling results in waveguide TE21(m1=−2)
left-handed forward waveTE31(m2=3) right-handed forward wave TE31(m2=3) right-handed backward wave 
下载: 导出CSV
-
[1] 胡银富, 冯进军. 用于雷达的新型真空电子器件[J]. 雷达学报, 2016, 5(4): 350-360 doi: 10.12000/JR16078Hu Yinfu, Feng Jinjun. New vacuum electronic devices for radar[J]. Journal of Radars, 2016, 5(4): 350-360 doi: 10.12000/JR16078 [2] 郑新, 刘超, 杨明. 大功率毫米波雷达及器件新技术研究[J]. 微波学报, 2020, 36(1): 62-66Zheng Xin, Liu Chao, Yang Ming. Research on new technology of high power millimeter wave radar and devices[J]. Journal of Microwaves, 2020, 36(1): 62-66 [3] Thumm M. History, presence and future of gyrotrons[C]//2009 IEEE International Vacuum Electronics Conference. 2009: 37-40. [4] Yang Jintao, Wang Efeng, Lei Chaojun, et al. Research on a Ka-band large-orbit gyro-TWT with periodic dielectric-loaded structure[J]. Electronics Letters, 2024, 60: e13068. doi: 10.1049/ell2.13068 [5] 杨锦涛. Ka波段大回旋电子注周期性介质加载结构回旋行波管研究[D]. 北京: 中国电子科技集团公司电子科学研究院, 2024Yang Jintao. Research on a a Ka-band large-orbit gyro-TWT with periodic dielectric-loaded structure[D]. Beijing: Institute of Electronic Science and Technology of China Electronics Technology Group Corporation, 2024 [6] Lei Z, Wang E, Yang J, et al. The comparative study of Gyro-TWT in large-orbit and small-orbit at second harmonic at Ka-band[C]//2024 IEEE International Conference on Plasma Science (ICOPS). 2024: 1. [7] Denisov G G, Bratman V L, Phelps A D R, et al. Gyro-TWT with a Helical operating waveguide: new possibilities to enhance efficiency and frequency bandwidth[C]//Proc. 21st Int Con infrared and Millimeter Waves. 1997: 289-290. [8] Denisov G G, Bratman V L, Cross A W, et al. Gyrotron traveling wave amplifier with a helical interaction waveguide[J]. Physical Review Letters, 1998, 81(25): 5680-5683. doi: 10.1103/PhysRevLett.81.5680 [9] 王峨锋. 螺旋波纹波导回旋行波管[D]. 成都: 电子科技大学, 2006Wang Efeng. Gyrotron traveling wave tube amplifier with the helical wave guide[D]. Chengdu: University of Electronic Science and Technology, 2006 [10] 黄宏嘉. 微波原理(卷Ⅰ)[M]. 北京: 科学出版社, 1963: 69-110Huang Hongjia. Microwave principles (Volume I)[M]. Beijing: Science Press, 1963: 69-110 [11] 王峨锋, 李宏福, 李浩, 等. 螺旋波纹波导研究[J]. 物理学报, 2005, 54(11): 5339-5343 doi: 10.3321/j.issn:1000-3290.2005.11.061Wang Efeng, Li Hongfu, Li Hao, et al. Study of the helical wave-guide[J]. Acta Physica Sinica, 2005, 54(11): 5339-5343 doi: 10.3321/j.issn:1000-3290.2005.11.061 [12] 钱景仁. 缓变参数不规则波导理论的补充及其应用[J]. 电子学报, 1963(1): 43-50Qian Jingren. Supplement to the theory of slow-varying number of irregular waveguides and its applications[J]. Acta Electronica Sinica, 1963(1): 43-50 [13] 钱景仁, 来芒, 黄宏嘉. 阻抗微扰概念在计算中继圆波导不规则性中的应用[J]. 电子学报, 1965(1): 67-72Qian Jingren, Lai Mang, Huang Hongjia. The concept of impedance-perturbation as applied to geometrical imperfections in circular waveguides in radio relay system[J]. Acta Electronica Sinica, 1965(1): 67-72 [14] 王哲远. Q波段无超导五折叠螺旋波纹波导回旋行波管研究[D]. 2022Wang Zheyuan. Q-band superconductivity-free five-fold spiral corrugated waveguide rotary traveling wave tube[D]. 2022 -
点击查看大图
计量
- 文章访问数: 4
- HTML全文浏览量: 3
- PDF下载量: 0
- 被引次数: 0
