X射线辐照典型材料出射电子特征规律研究

韩立会; 朱金辉; 王建国; 牛胜利; 刘利; 左应红

doi:10.11884/HPLPB202537.250215

X射线辐照典型材料出射电子特征规律研究

doi: 10.11884/HPLPB202537.250215

西北核技术研究所，西安 710024

基金项目: 国家重点研发计划资助项目(2020YFA0709800)

详细信息

作者简介:
韩立会，hanlihui@nint.ac.cn

通讯作者:
王建国，wangjianguo@nint.ac.cn。

中图分类号: O571.33
计量
- 文章访问数: 8
- HTML全文浏览量: 4
- PDF下载量: 0
- 被引次数: 0
出版历程
- 收稿日期: 2025-07-15
- 修回日期: 2025-08-21
- 录用日期: 2025-08-19
- 网络出版日期: 2025-09-02

Investigation of emitted electron characteristics from typical materials under X-ray irradiation

Northwest Institute of Nuclear Technology, P. O. Box 69-12, Xi'an 710024, China

摘要

摘要: 电子发射参数是研究X射线辐照下腔体结构产生系统电磁脉冲(SGEMP)效应的关键电流源项。采用基于浓缩历史方法与单事件方法建立的电子输运模块开展光子-电子耦合输运蒙特卡罗模拟计算。通过分析光子、电子与物质相互作用特点，系统分析了不同能量X射线正入射辐照典型材料时产生的背向及前向电子发射特性，包括电子能谱、角分布规律。建立基于光子平均自由程的背向电子产额计算方法，提出了饱和产额计算公式与饱和厚度；针对前向电子产额，结合光子衰减规律和电子最大射程建立了计算模型，并引入累积因子进行修正，进一步提升了准确性。在SGEMP关注的X射线能量范围及典型材料厚度范围内进行验证，结果显示，与蒙特卡罗直接模拟相比，计算公式给出的背向、前向电子产额相对偏差在10%以内，研究结果为SGEMP的电子产额计算提供了一种高效便捷的求解方法。
- X射线 /
- 光电子 /
- 康普顿散射电子 /
- 蒙特卡罗 /
- 系统电磁脉冲 /
- 111111 /
- 111111
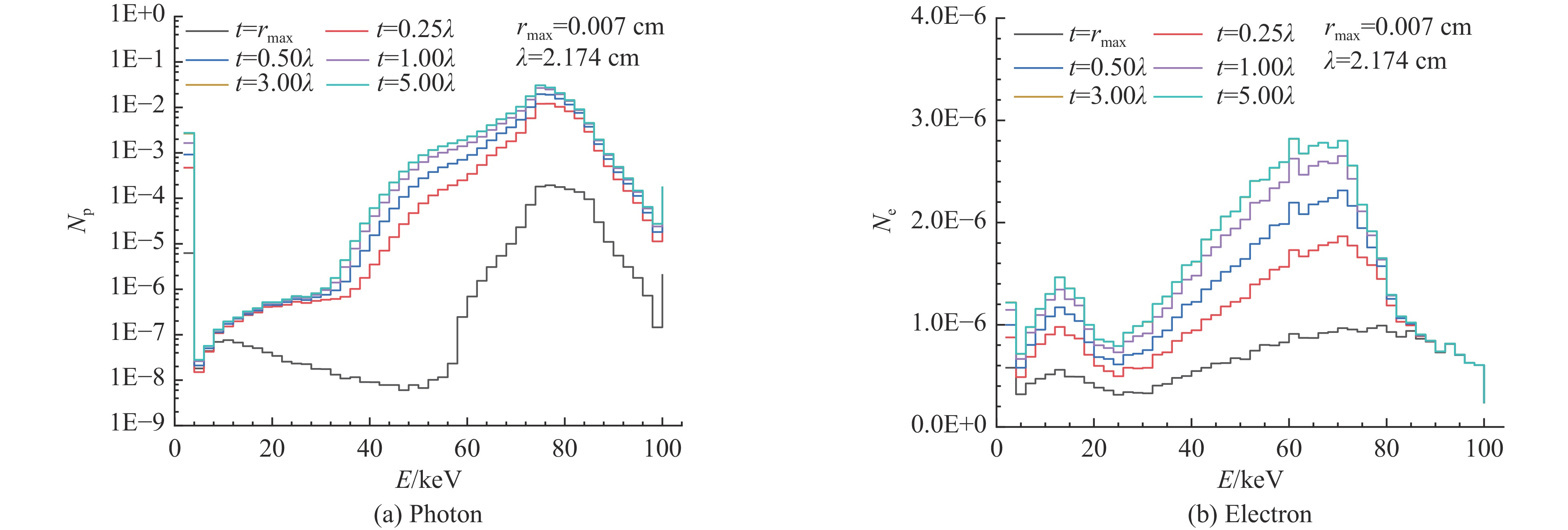
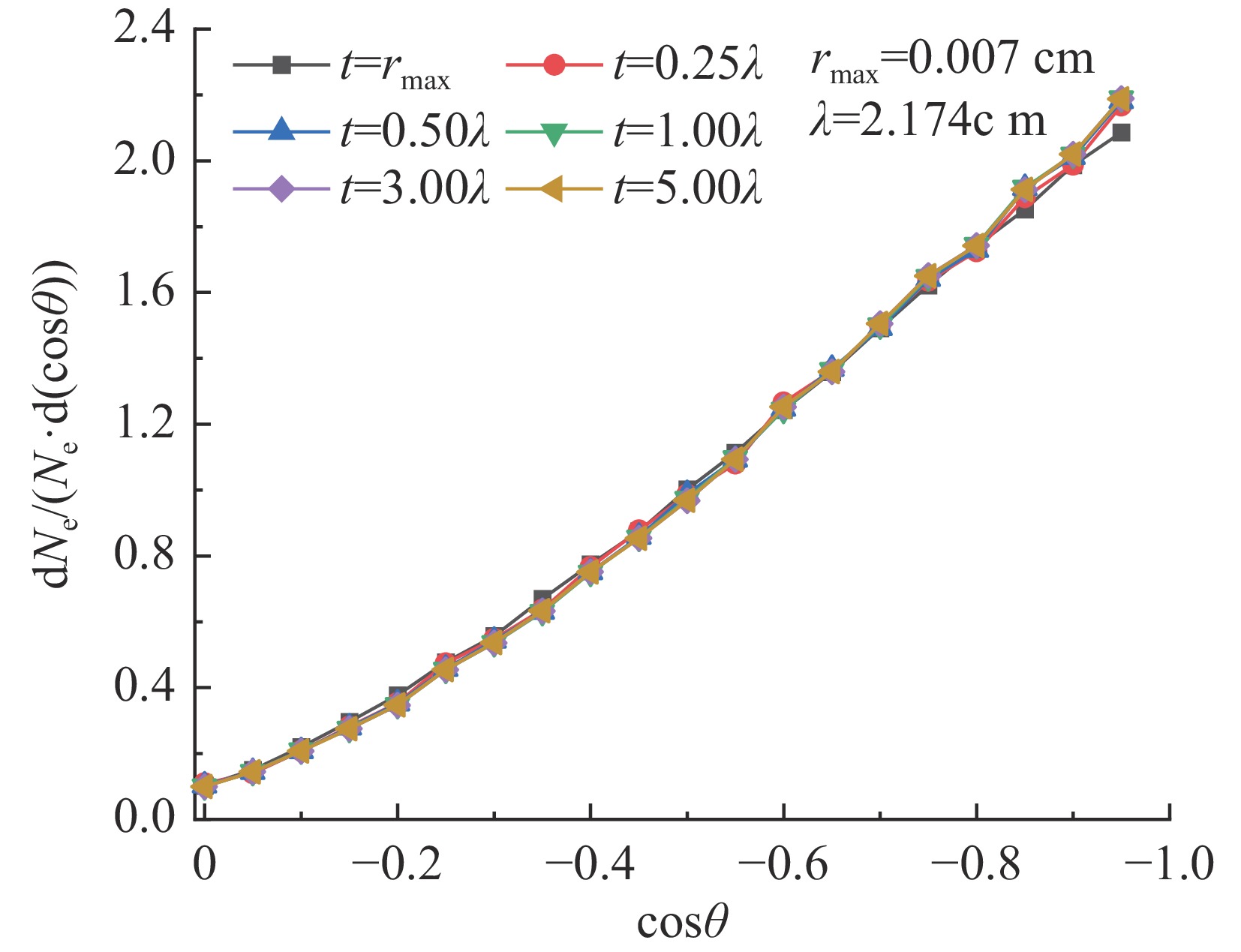
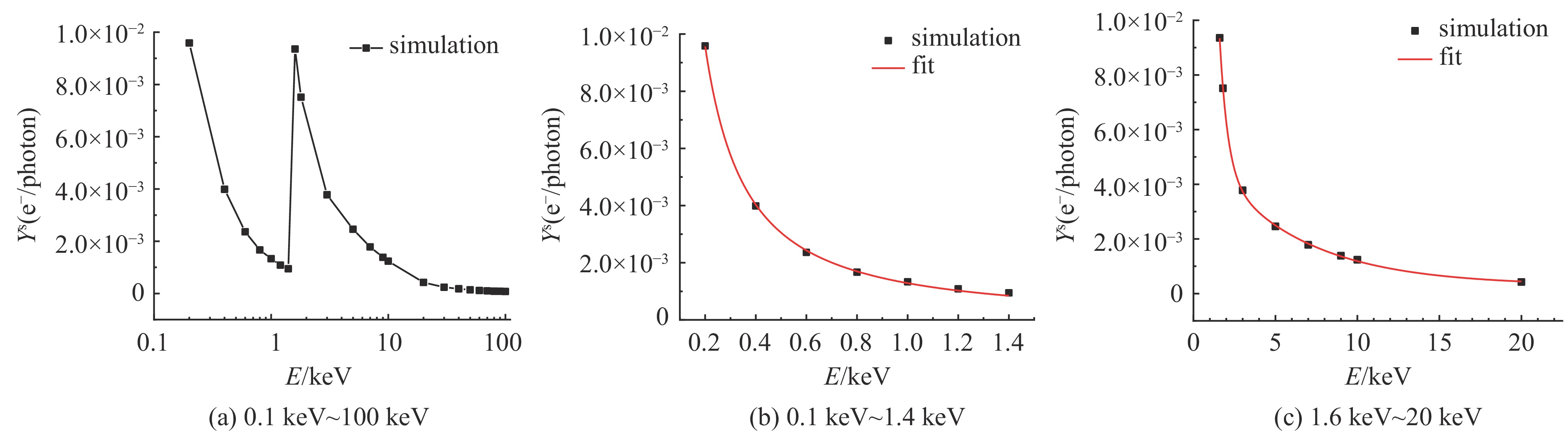
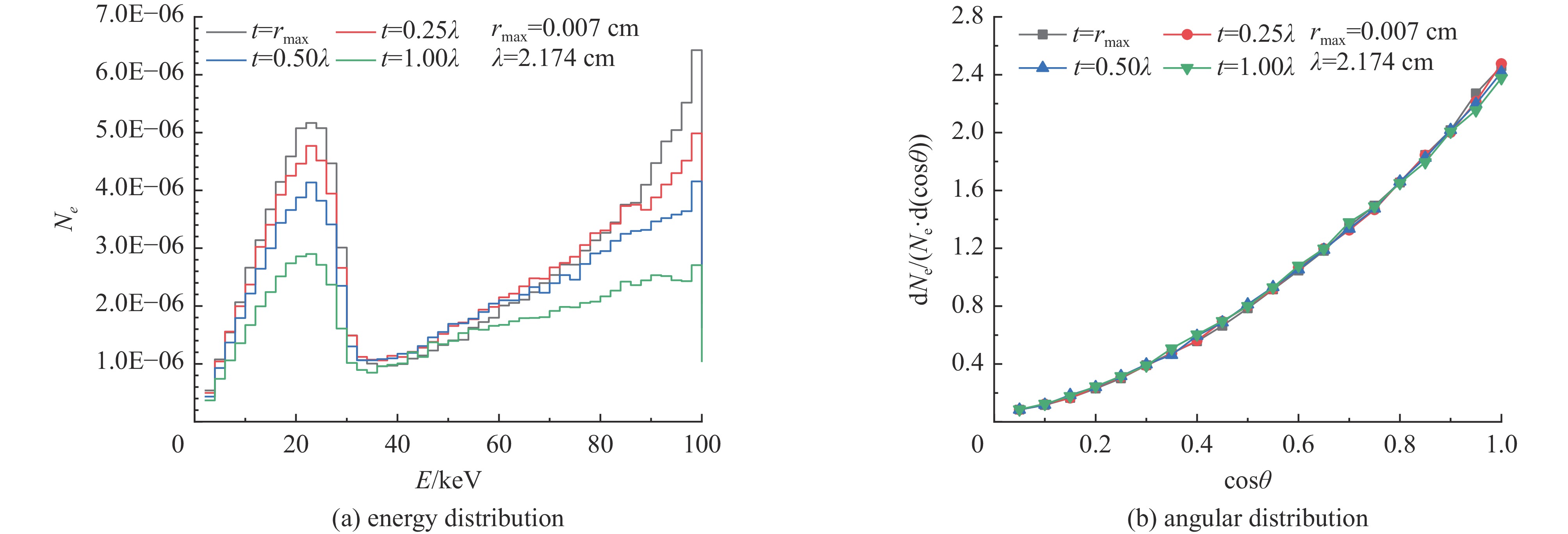
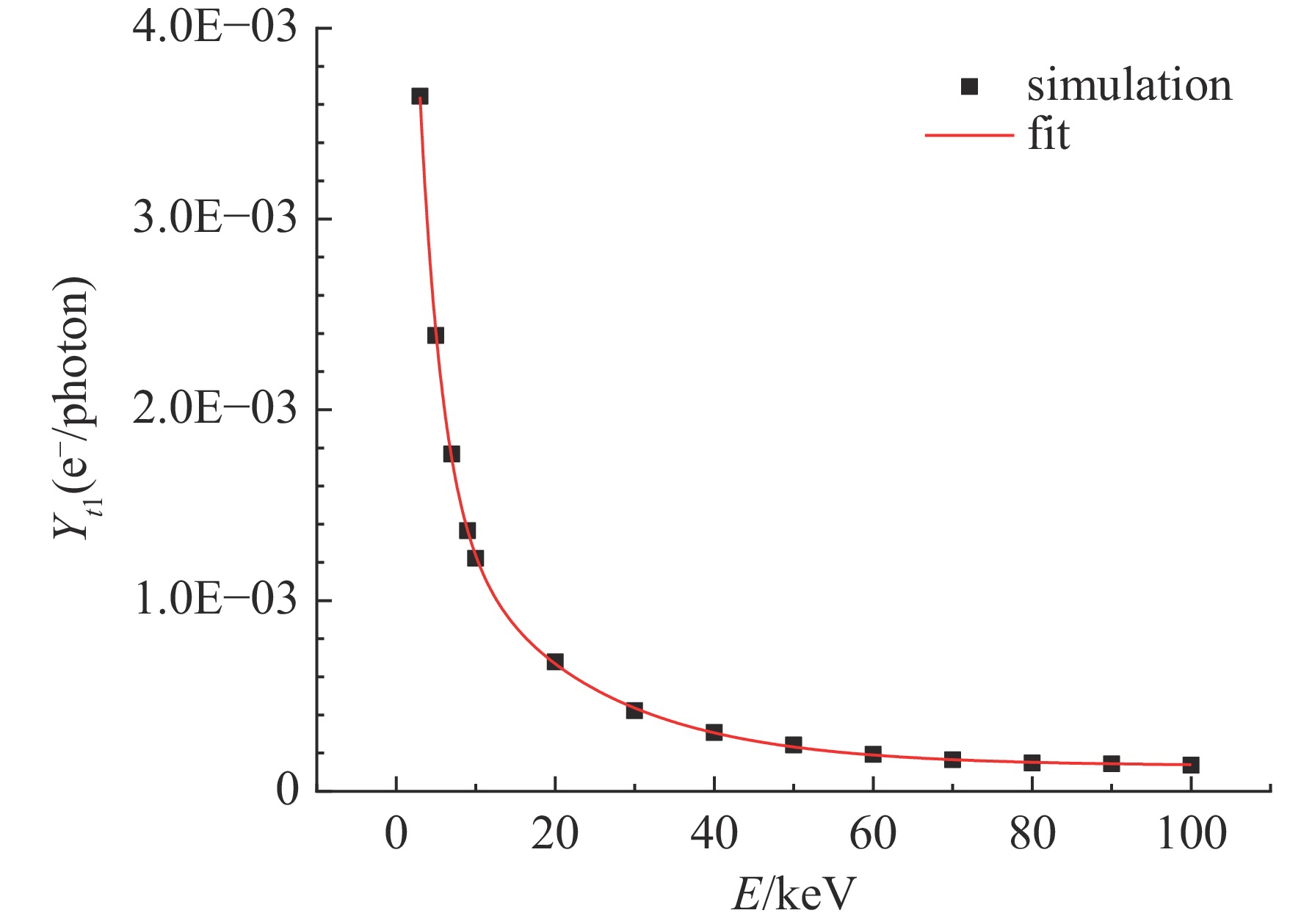
Abstract: Background
System-generated electromagnetic pulse (SGEMP) effects induced by X-ray irradiation pose a significant threat to electronic systems in aerospace and nuclear environments. Accurate quantification of electron emission parameters, which are critical current sources for SGEMP simulation, remains challenging because of the complex coupled photon-electron transport processes involved.
Purpose
This study aims to systematically investigate the characteristics of backward- and forward-emitted electrons from typical materials (e.g., aluminum) under X-ray irradiation and develop efficient analytical models for predicting electron yields without relying on computationally intensive Monte Carlo (MC) simulations for each new scenario.
Methods
Photon-electron coupled transport simulations were performed using a Monte Carlo module combining the condensed history and single-event methods. The energy and angular distributions of emitted electrons were analyzed for X-rays (0.1–100 keV) normally incident on aluminum plates of varying thicknesses. Analytical models for backward and forward electron yields were derived based on photon mean free path, electron maximum range, and attenuation laws, with a cumulative correction factor introduced to improve forward yield accuracy.
Results
Backward electron energy spectra exhibited a double-peak structure (Compton and photoelectron peaks), with angular distributions following a cosine law. A saturation thickness of～3 photon mean free paths was identified for backward yield, beyond which yields remained constant. For forward emission, yields peaked at the electron maximum range thickness and decreased with further increasing plate thickness. The proposed analytical formulas for both backward and forward yields achieved relative errors within 10% compared to direct MC simulations across the studied energy and thickness ranges.
Conclusions
The derived analytical models provide efficient and accurate predictions of electron emission coefficients for SGEMP source terms, reducing the need for repeated MC simulations. The methodology is generalizable to other materials and supports rapid assessment of X-ray-induced electron emission in complex systems. Future work will explore machine learning techniques to further enhance computational efficiency for broader applications.
- X-ray /
- photoelectron /
- Compton electron /
- Monte Carlo simulation /
- system-generated electromagnetic pulse /
- electron yield /
- analytical model

HTML全文

图 1 计算模型示意图

Figure 1. Schematic diagram of the computational model

下载: 全尺寸图片幻灯片

图 2 光子与铝原子的相互作用参数

Figure 2. Photon interaction parameters with aluminum atoms

下载: 全尺寸图片幻灯片

图 3 电子在铝介质中的射程图

Figure 3. Electron range in aluminum medium

下载: 全尺寸图片幻灯片

图 4 平板内部对表面出射电子有贡献的区域示意图

Figure 4. Schematic of regions contributing to surface-emitted electrons within the plate

下载: 全尺寸图片幻灯片

图 5 背向出射光子、电子能谱

Figure 5. Energy distributions of backward-emitted photons and electrons

下载: 全尺寸图片幻灯片

图 6 背向出射电子角分布

Figure 6. Angular Distribution of Backward-Emitted Electrons

下载: 全尺寸图片幻灯片

图 7 不同能量X射线入射背向出射电子的饱和产额

Figure 7. Saturation yields of backward-emitted electrons under X-rays of varying energies

下载: 全尺寸图片幻灯片

图 8 前向出射电子特征

Figure 8. Characteristics of forward-emitted electrons

下载: 全尺寸图片幻灯片

图 9 前向最大电子产额

Figure 9. Maximum forward electron yield

下载: 全尺寸图片幻灯片

图 10 累积因子修正函数曲线

Figure 10. Cumulative factor correction function curve

下载: 全尺寸图片幻灯片

表 1 不同能量X射线入射不同厚度铝板背向出射电子产额

Table 1. Backward electron yields for aluminum plates of varying thicknesses under different X-ray energies

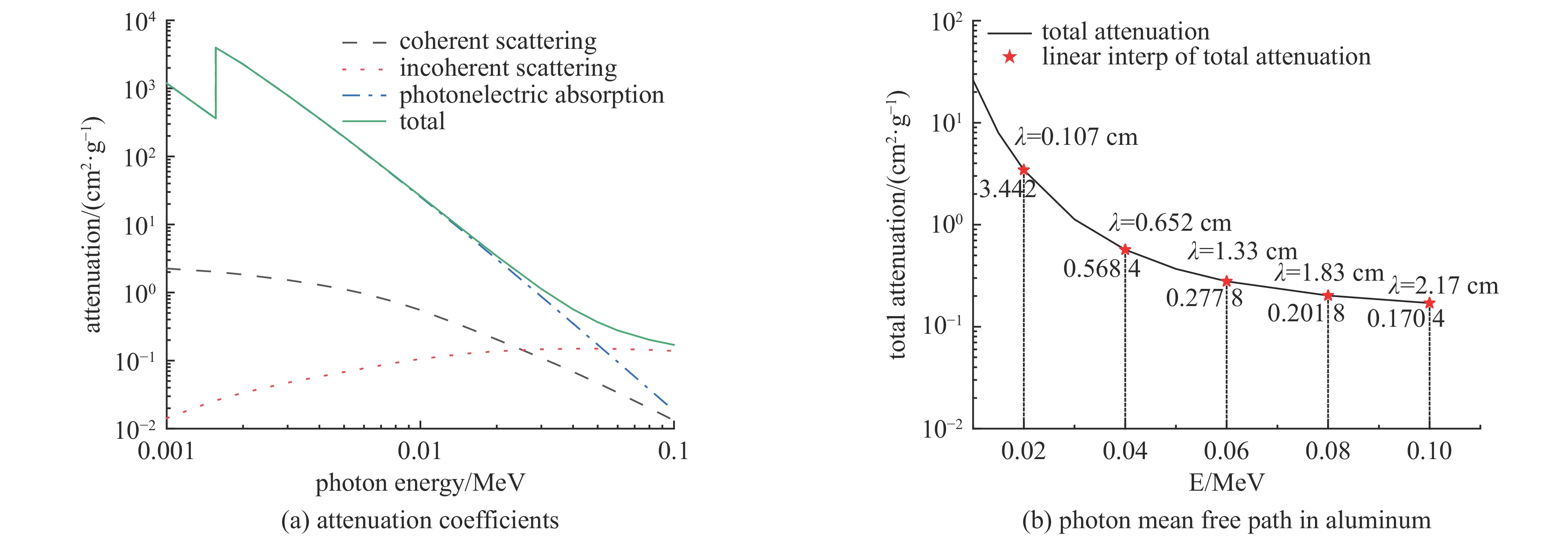
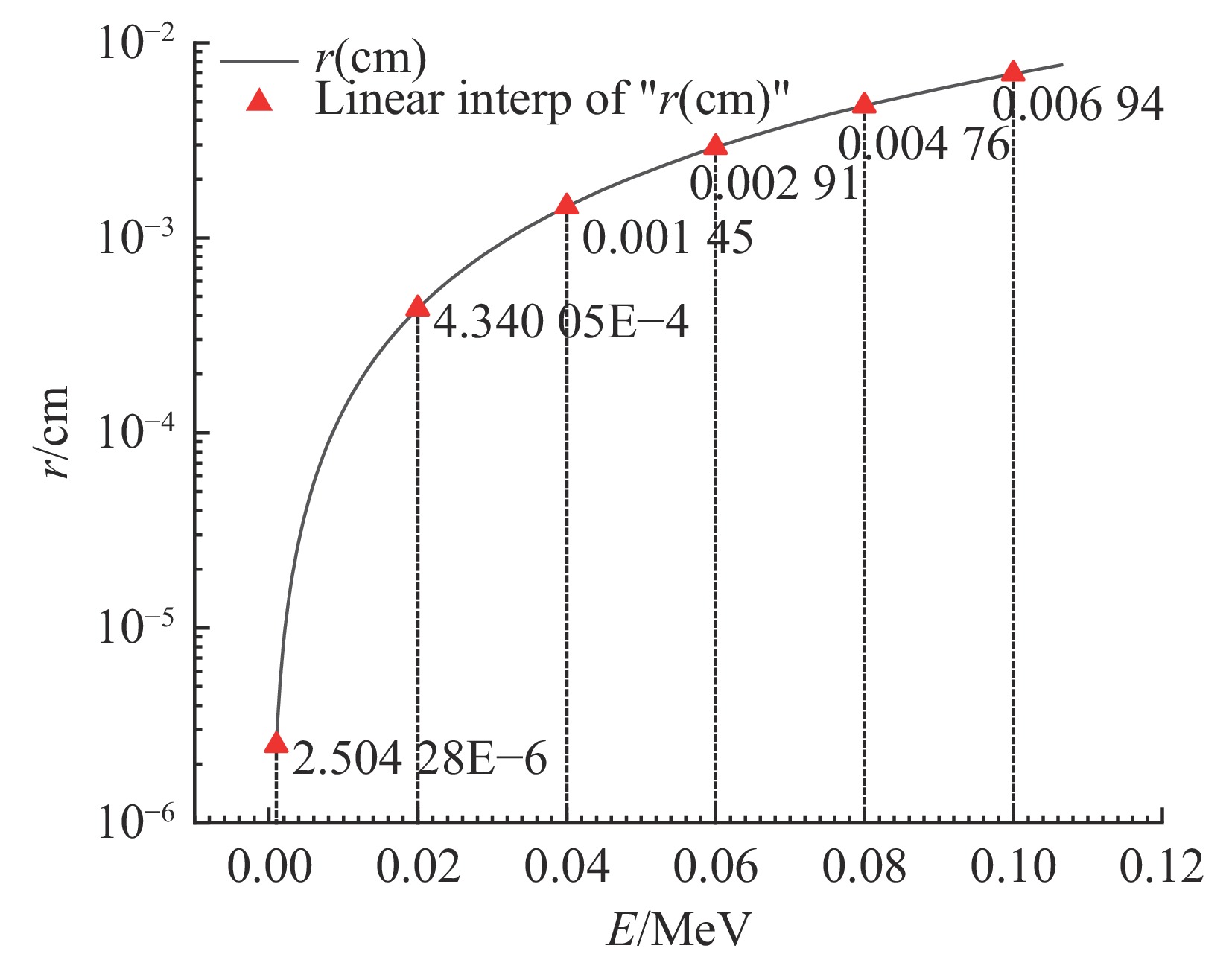
E/keV	r_max/cm	$ \lambda ({\text{cm}}) $	$ {Y_{{r_{\max }}}} $	$ {Y_{0.25\lambda }} $	$ {Y_{0.5\lambda }} $	$ {Y_{0.75\lambda }} $	$ {Y_\lambda } $	$ {Y_{3\lambda }} $	$ {Y_{5\lambda }} $
1	2.93×10⁻⁶	3.13×10⁻⁴	1.33×10⁻³	1.33×10⁻³	1.33×10⁻³	1.33×10⁻³	1.33×10⁻³	1.33×10⁻³	1.33×10⁻³
5	4.05×10⁻⁵	1.92×10⁻³	2.45×10⁻³	2.46×10⁻³	2.46×10⁻³	2.46×10⁻³	2.46×10⁻³	2.46×10⁻³	2.46×10⁻³
10	1.31×10⁻⁴	1.41×10⁻²	1.23×10⁻³	1.24×10⁻³	1.24×10⁻³	1.24×10⁻³	1.24×10⁻³	1.24×10⁻³	1.24×10⁻³
20	4.34×10⁻⁴	1.08×10⁻¹	4.12×10⁻⁴	4.18×10⁻⁴	4.21×10⁻⁴	4.22×10⁻⁴	4.23×10⁻⁴	4.24×10⁻⁴	4.24×10⁻⁴
40	1.44×10⁻³	6.52×10⁻¹	1.50×10⁻⁴	1.67×10⁻⁴	1.73×10⁻⁴	1.77×10⁻⁴	1.78×10⁻⁴	1.80×10⁻⁴	1.80×10⁻⁴
60	2.91×10⁻³	1.33	7.42×10⁻⁵	9.43×10⁻⁵	1.04×10⁻⁴	1.10×10⁻⁴	1.12×10⁻⁴	1.16×10⁻⁴	1.16×10⁻⁴
80	4.76×10⁻³	1.84	4.53×10⁻⁵	6.58×10⁻⁵	7.52×10⁻⁵	7.98×10⁻⁵	8.25×10⁻⁵	8.62×10⁻⁵	8.65×10⁻⁵
100	6.94×10⁻³	2.17	3.13×10⁻⁵	5.33×10⁻⁵	6.43×10⁻⁵	7.08×10⁻⁵	7.40×10⁻⁵	7.88×10⁻⁵	7.88×10⁻⁵

下载: 导出CSV

表 2 给定能量、平板厚度条件下背向产额的蒙卡模拟值与计算公式对比

Table 2. Comparison between Monte Carlo simulations and analytical formula predictions for backward electron yields at given energies and plate thicknesses

E/keV	Y_MC	Y_Eq	RE/%	Y_MC	Y_Eq	RE/%	Y_MC	Y_Eq	RE/%
E/keV	t=0.075mm			t=0.5mm			t=2.5mm
0.5	2.99×10⁻³	3.07×10⁻³	2.78	2.99×10⁻³	3.07×10⁻³	2.78	2.99×10⁻³	3.07×10⁻³	−2.71
3	3.78×10⁻³	3.74×10⁻³	−1.06	3.78×10⁻³	3.74×10⁻³	−1.06	3.78×10⁻³	3.74×10⁻³	−1.06
6	2.09×10⁻³	2.13×10⁻³	1.73	2.09×10⁻³	2.13×10⁻³	1.72	2.09×10⁻³	2.13×10⁻³	1.72
9	1.38×10⁻³	1.36×10⁻³	−1.44	1.38×10⁻³	1.36×10⁻³	−1.51	1.38×10⁻³	1.36×10⁻³	−1.51
15	6.24×10⁻⁴	6.58×10⁻⁴	5.35	6.29×10⁻⁴	6.58×10⁻⁴	4.64	6.29×10⁻⁴	6.58×10⁻⁴	4.61
35	1.84×10⁻⁴	1.95×10⁻⁴	6.03	1.90×10⁻⁴	2.01×10⁻⁴	5.33	2.02×10⁻⁴	2.15×10⁻⁴	5.98
55	8.86×10⁻⁵	8.59×10⁻⁵	−3.07	9.39×10⁻⁵	8.95×10⁻⁵	−4.72	1.07×10⁻⁴	1.02×10⁻⁴	−4.61
75	5.17×10⁻⁵	5.05×10⁻⁵	−2.38	5.50×10⁻⁵	5.31×10⁻⁵	−3.37	6.61×10⁻⁵	6.36×10⁻⁵	−3.80
95	3.47×10⁻⁵	3.83×10⁻⁵	10.11	3.75×10⁻⁵	4.04×10⁻⁵	7.67	4.66×10⁻⁵	4.91×10⁻⁵	5.57

下载: 导出CSV

表 3 40keV光子入射不同厚度平板三种方式得到前向出射电子产额结果对比

Table 3. Comparison of forward electron yields obtained via three methods for 40 keV photons incident on plates of varying thicknesses

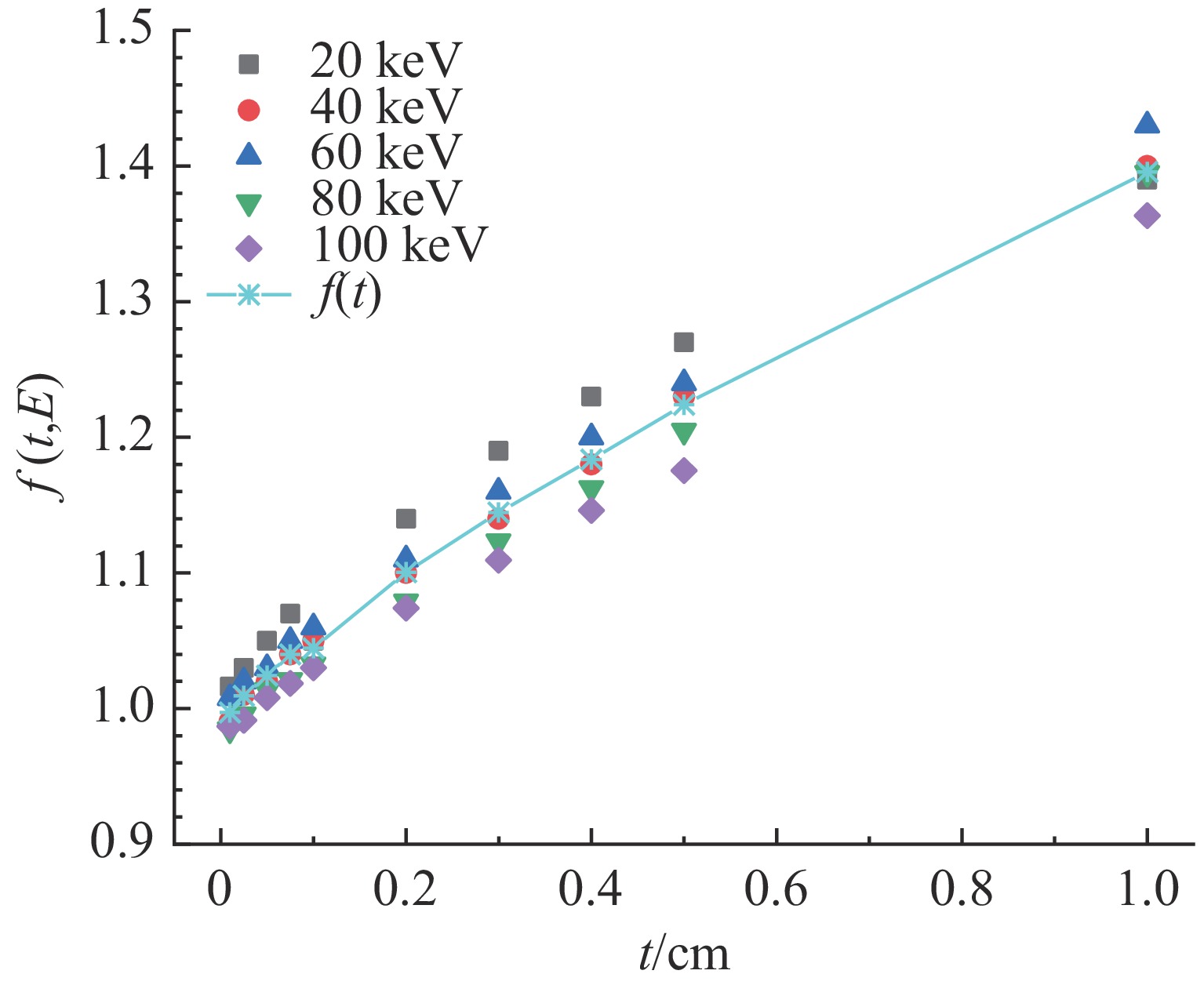
t/mm	Y_MC	Y_Eq6	RE/%	Y_Eq8	RE/%
0.10	3.01×10⁻⁴	3.03×10⁻⁴	0.96	3.04×10⁻⁴	1.10
0.25	2.98×10⁻⁴	2.96×10⁻⁴	−0.55	2.99×10⁻⁴	0.37
0.50	2.92×10⁻⁴	2.85×10⁻⁴	−2.18	2.92×10⁻⁴	0.01
0.75	2.85×10⁻⁴	2.75×10⁻⁴	−3.51	2.84×10⁻⁴	−0.11
1.00	2.77×10⁻⁴	2.64×10⁻⁴	−4.73	2.77×10⁻⁴	−0.16
2.00	2.49×10⁻⁴	2.27×10⁻⁴	−8.95	2.49×10⁻⁴	−0.14
3.00	2.22×10⁻⁴	1.94×10⁻⁴	−12.41	2.22×10⁻⁴	0.08
4.00	1.97×10⁻⁴	1.67×10⁻⁴	−15.57	1.98×10⁻⁴	0.11
5.00	1.75×10⁻⁴	1.43×10⁻⁴	−18.44	1.75×10⁻⁴	0.01
10.00	9.30×10⁻⁵	6.64×10⁻⁵	−28.63	9.26×10⁻⁵	−0.44

下载: 导出CSV

表 4 给定能量、平板厚度条件下前向电子产额的蒙卡模拟值与计算公式对比

Table 4. Comparison between Monte Carlo simulations and analytical formula predictions for forward electron yields at given energies and plate thicknesses

E/keV	Y_MC(e-)	Y_eq	RE/%	Y_MC	Y_eq	RE/%	Y_MC	Y_eq	RE/%
E/keV	t=0.075 mm			t=0.5 mm			t=2.5 mm
3	0	4.42×10⁻¹⁰	−	0	2.40×10⁻⁴⁹	−	0	0	−
6	1.98×10⁻⁴	1.99×10⁻⁴	0.86	0	3.66×10⁻¹⁰	−	0	3.65×10⁻³⁷	−
9	6.79×10⁻⁴	6.36×10⁻⁴	−6.41	8.80×10⁻⁶	8.05×10⁻⁶	−8.52	0	9.37×10⁻¹⁵	−
15	8.18×10⁻⁴	7.40×10⁻⁴	−9.56	3.40×10⁻⁴	3.04×10⁻⁴	−10.79	4.88×10⁻⁶	4.53×10⁻⁶	−7.21
35	3.57×10⁻⁴	3.58×10⁻⁴	0.32	3.43×10⁻⁴	3.32×10⁻⁴	−3.19	2.45×10⁻⁴	2.30×10⁻⁴	−6.08
55	2.12×10⁻⁴	2.08×10⁻⁴	−1.82	2.09×10⁻⁴	2.05×10⁻⁴	−2.02	1.94×10⁻⁴	1.89×10⁻⁴	−2.64
75	1.56×10⁻⁴	1.58×10⁻⁴	1.20	1.58×10⁻⁴	1.58×10⁻⁴	−0.02	1.54×10⁻⁴	1.53×10⁻⁴	−0.25
95	1.40×10⁻⁴	1.42×10⁻⁴	1.21	1.41×10⁻⁴	1.42×10⁻⁴	0.99	1.37×10⁻⁴	1.41×10⁻⁴	3.07

下载: 导出CSV

参考文献(23)

[1]	孟萃. 瞬态电离辐射激励强电磁脉冲[M]. 北京: 清华大学出版社, 2022: 85 Meng Cui. Transient ionizing radiation induced intense electromagnetic pulse[M]. Beijing: Tsinghua University Press, 2022: 85
[2]	王建国, 刘利, 牛胜利, 等. 高空核爆炸环境数值模拟[J]. 现代应用物理, 2023, 14: 010101 doi: 10.12061/j.issn.2095-6223.2023.010101 Wang Jianguo, Liu Li, Niu Shengli, et al. Numerical simulations of environmental parameters of high-altitude nuclear explosion[J]. Modern Applied Physics, 2023, 14: 010101 doi: 10.12061/j.issn.2095-6223.2023.010101
[3]	Wang Jianguo, Liu Li, Zuo Yinghong, et al. Research progress in numerical simulation of environmental parameters generated by the high-altitude nuclear explosions[J]. IEEE Transactions on Nuclear Science, 2025, 72(3): 884-900. doi: 10.1109/TNS.2025.3530013
[4]	陈剑楠, 陶应龙, 牛胜利. X射线辐照圆柱腔体SGEMP电子发射参数的计算[J]. 现代应用物理, 2020, 11: 010501 doi: 10.12061/j.issn.2095-6223.2020.010501 Chen Jiannan, Tao Yinglong, Niu Shengli. Calculation of electron emission parameter of SGEMP in cylinder cavity irradiated by X-rays[J]. Modern Applied Physics, 2020, 11: 010501 doi: 10.12061/j.issn.2095-6223.2020.010501
[5]	Dolan K W. X-ray-induced electron emission from metals[J]. Journal of Applied Physics, 1975, 46(6): 2456-2463. doi: 10.1063/1.322229
[6]	Bernstein M J, Paschen K W. Forward and backward photoemission yields from metals at various X-ray angles of incidence[J]. IEEE Transactions on Nuclear Science, 1973, 20(6): 111-116. doi: 10.1109/TNS.1973.4327380
[7]	Chadsey W L, Wilson C W, Pine V W. X-ray photoemission calculations[J]. IEEE Transactions on Nuclear Science, 1975, 22(6): 2345-2350. doi: 10.1109/TNS.1975.4328131
[8]	Dellin T A, MacCallum C J. Photo-Compton currents emitted from a surface[J]. Journal of Applied Physics, 1975, 46(7): 2924-2934. doi: 10.1063/1.322022
[9]	Dellin T A, Huddleston R E, MacCallum C J. Second generation analytical photo-Compton current methods[J]. IEEE Transactions on Nuclear Science, 1975, 22(6): 2549-2555. doi: 10.1109/TNS.1975.4328166
[10]	朱金辉, 左应红, 刘利, 等. 蒙特卡罗方法在核爆辐射环境模拟中的应用与发展[J]. 现代应用物理, 2023, 14: 030104 Zhu Jinhui, Zuo Yinghong, Liu Li, et al. Application and development of Monte Carlo method in simulation of nuclear explosion radiation environment[J]. Modern Applied Physics, 2023, 14: 030104
[11]	张含天, 陈剑楠, 周前红, 等. 系统电磁脉冲建模与数值模拟研究进展[J]. 电波科学学报, 2024, 39(5): 797-807 doi: 10.12265/j.cjors.2024034 Zhang Hantian, Chen Jiannan, Zhou Qianhong, et al. Progress in modeling and numerical simulation of system generated electromagnetic pulse[J]. Chinese Journal of Radio Science, 2024, 39(5): 797-807 doi: 10.12265/j.cjors.2024034
[12]	孙会芳, 易涛, 董志伟, 等. 神光装置辐照腔体系统电磁脉冲的数值模拟[J]. 强激光与粒子束, 2024, 36: 043024 doi: 10.11884/HPLPB202436.230273 Sun Huifang, Yi Tao, Dong Zhiwei, et al. Simulation of cavity system generated electromagnetic pulse radiated by SG-facility[J]. High Power Laser and Particle Beams, 2024, 36: 043024 doi: 10.11884/HPLPB202436.230273
[13]	李进玺, 吴伟, 郭景海, 等. “闪光二号”环境中系统电磁脉冲计算模型的验证[J]. 现代应用物理, 2016, 7: 030503 doi: 10.3969/j.issn.2095-6223.2016.03.005 Li Jinxi, Wu Wei, Guo Jinghai, et al. Verification of numerical simulation model for SGEMP generated in flash-Ⅱ accelerator environment[J]. Modern Applied Physics, 2016, 7: 030503 doi: 10.3969/j.issn.2095-6223.2016.03.005
[14]	陈剑楠, 陶应龙, 陈再高, 等. 系统电磁脉冲模拟中的发射电子参数计算[J]. 现代应用物理, 2018, 9: 040501 doi: 10.12061/j.issn.2095-6223.2018.040501 Chen Jiannan, Tao Yinglong, Chen Zaigao, et al. Calculation of emission electron parameter in simulation of SGEMP[J]. Modern Applied Physics, 2018, 9: 040501 doi: 10.12061/j.issn.2095-6223.2018.040501
[15]	Chen Jiannan, Wang Jianguo, Tao Yinglong, et al. Simulation of SGEMP using particle-in-cell method based on conformal technique[J]. IEEE Transactions on Nuclear Science, 2019, 66(5): 820-826. doi: 10.1109/TNS.2019.2911933
[16]	Bradford J N. X-ray induced electron emission II[J]. IEEE Transactions on Nuclear Science, 1973, 20(6): 105-110. doi: 10.1109/TNS.1973.4327379
[17]	Woods A J, Wenaas E P. Photon source SGEMP spectrum evaluations[R]. Sandia National Laboratories, 1978.
[18]	Storm L, Israel H I. Photon cross sections from 1 keV to 100 MeV for elements Z=1 to Z=100[J]. Atomic Data and Nuclear Data Tables, 1970, 7(6): 565-681. doi: 10.1016/S0092-640X(70)80017-1
[19]	Berger M J. Monte Carlo calculation of the penetration and diffusion of fast charged particles[M]//Alder B, Fernbach S, Rotenberg M. Methods in Computational Physics, Vol. 1. New York: Academic Press, 1963: 135.
[20]	Seltzer S M. Cross sections for bremsstrahlung production and electron-impact ionization[M]//Jenkins T M, Nelson W R, Rindi A. Monte Carlo Transport of Electrons and Photons. Boston: Springer, 1988: 81.
[21]	夏益华. 高等电离辐射防护教程[M]. 哈尔滨: 哈尔滨工程大学出版社, 2010: 87 Xia Yihua. Advanced course on ionizing radiation protection[M]. Harbin: Harbin Engineering University Press, 2010: 87
[22]	乔海亮, 谢海燕, 刘钰. 基于人工神经网络的HEMP-E1环境快速预测模型[J]. 现代应用物理, 2025, 16: 011318 doi: 10.12061/j.issn.2095-6223.202501011 Qiao Hailiang, Xie Haiyan, Liu Yu. A fast prediction model for HEMP-E1 environment based on artificial neural network[J]. Modern Applied Physics, 2025, 16: 011318 doi: 10.12061/j.issn.2095-6223.202501011
[23]	游检卫, 张嘉男, 刘彻, 等. 智能计算电磁学及其超材料智能设计应用[J]. 现代应用物理, 2025, 16: 011301 doi: 10.12061/j.issn.2095-6223.202412045 You Jianwei, Zhang Jianan, Liu Che, et al. Intelligent computational electromagnetics and its applications in intelligent design of metamaterials[J]. Modern Applied Physics, 2025, 16: 011301 doi: 10.12061/j.issn.2095-6223.202412045