Rhodotron加速器工业CT检测高密度工件的高分辨重建算法研究

李奉笑; 杨润; 孙志强; 钟国威; 刘成峰; 何小中; 阳庆国; 周日峰

doi:10.11884/HPLPB202537.250263

Rhodotron加速器工业CT检测高密度工件的高分辨重建算法研究

doi: 10.11884/HPLPB202537.250263

1.
重庆大学光电技术及系统教育部重点实验室 ICT研究中心，重庆 400044
2.
中国工程物理研究院流体物理研究所，四川绵阳 621900

基金项目: 国家自然科学基金重大科研仪器研制项目（11827809）；冲击波物理与爆轰物理全国重点实验室基金项目（2024CXPJGFJJ06411）

详细信息

作者简介:
李奉笑，lfx@cqu.edu.cn

通讯作者:
周日峰，zhou65112401@cqu.edu.cn。

中图分类号: TP391
计量
- 文章访问数: 43
- HTML全文浏览量: 23
- PDF下载量: 4
- 被引次数: 0
出版历程
- 收稿日期: 2025-08-18
- 修回日期: 2025-10-11
- 录用日期: 2025-10-08
- 网络出版日期: 2025-10-23

High-resolution reconstruction algorithm for high-density workpiece inspection in rhodotron-based industrial CT

1.
Engineering Research Center of Industrial Computed Tomography Nondestructive Testing, Ministry of Education, Chongqing University, Chongqing 400044, China
2.
Institute of Fluid Physics, CAEP, Mianyang 621900, China

摘要

摘要: Rhodotron加速器因其微焦点特性，为工业计算机断层扫描（CT）系统实现高空间分辨率检测提供了硬件基础。然而，在检测航空航天等领域常用的高密度、大尺寸工件时，X射线的强衰减会导致投影数据信噪比严重降低，常规重建算法难以兼顾噪声抑制与细节保持，限制了系统分辨能力的发挥。针对此问题，旨在提出一种能够在强噪声背景下实现高保真重建的算法。本研究提出一种基于双边总变分正则化凸集投影（POCS-BTV）的高分辨迭代重建算法。该算法在POCS框架内，创新性地引入具有优越边缘保持能力的BTV作为正则项，通过迭代优化有效分离图像结构与噪声。通过仿真实验和基于Rhodotron加速器CT系统的实际物理模体实验对算法性能进行验证，并与SIRT、POCS-TV及POCS-RTV等算法进行对比。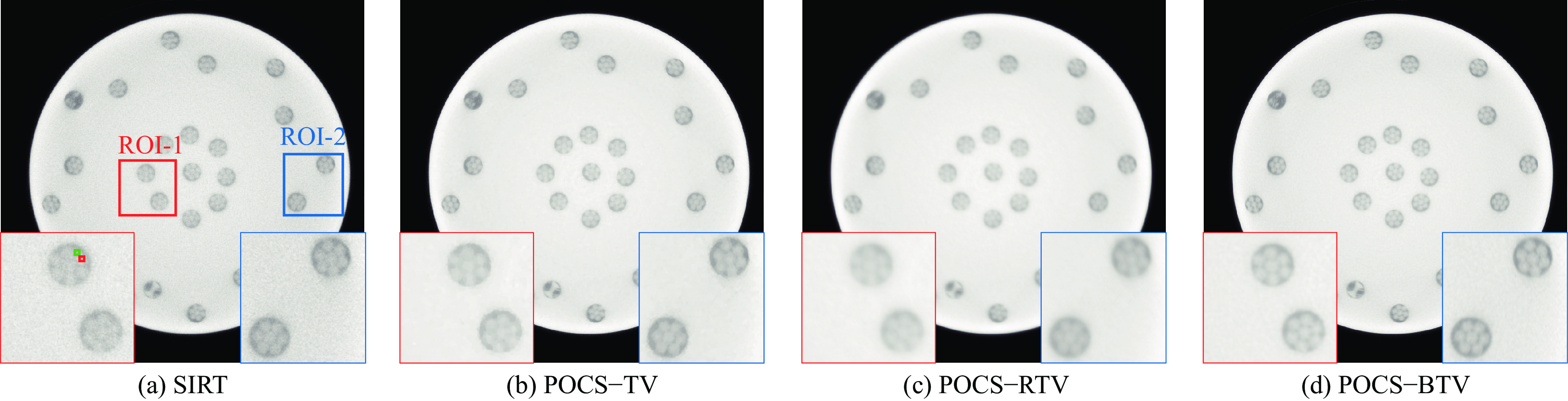仿真实验结果表明，所提POCS-BTV算法重建的Shepp-Logan头模图像峰值信噪比（PSNR）达到30.76，结构相似性（SSIM）为0.8405，在各项评价指标上均表现出显著优势。针对直径70 mm高强度钢丝缆绳模体的实际数据重建，POCS-BTV算法的重建图像能够清晰分辨钢丝间的微小缝隙，有效避免了其他算法中出现的结构混叠与边缘模糊现象。研究证实，POCS-BTV算法能充分利用Rhodotron加速器的硬件优势，在强噪声背景下实现高密度工件内部微观结构的高分辨、高保真重建，为关键工业部件的精密无损检测提供了可靠的解决方案。
- Rhodotron加速器 /
- 工业计算机断层扫描 /
- CT图像重建 /
- 双边总变分 /
- 无损检测
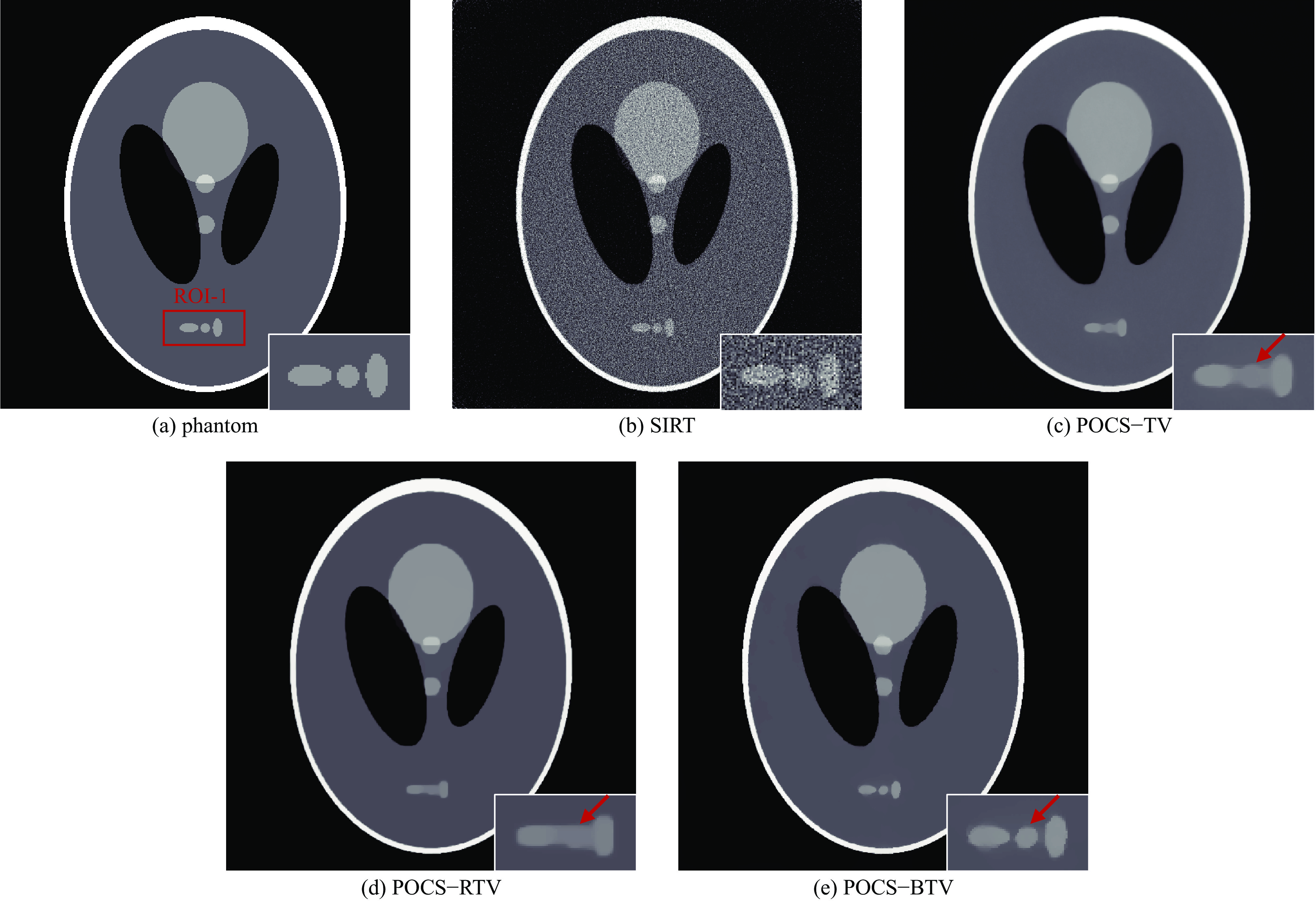
Abstract: Background
High-resolution industrial computed tomography (CT) is crucial for the non-destructive testing (NDT) of critical components, particularly in the aerospace industry where high-density materials are common. The Rhodotron accelerator, with its micro-focus capability, offers a hardware advantage for achieving high spatial resolution over traditional linear accelerators. However, its potential is severely hampered when inspecting large, high-density workpieces. The strong X-ray attenuation leads to projection data with a very low signal-to-noise ratio (SNR), causing conventional reconstruction algorithms to either produce noisy images or oversmooth critical details, thereby limiting the system's effective resolution.
Purpose
This study aims to develop and validate a reconstruction algorithm capable of overcoming the low-SNR challenge inherent in Rhodotron CT scans of high-density objects. The primary objective is to achieve high-resolution, high-fidelity image reconstruction that effectively suppresses noise while preserving the fine structural edges essential for accurate defect detection.
Methods
A novel iterative algorithm, termed Projections Onto Convex Sets regularized by Bilateral Total Variation (POCS-BTV), is proposed. The algorithm integrates BTV, a regularizer known for its superior edge-preservation properties, into the POCS framework to constrain the solution during iterations. The performance of POCS-BTV was evaluated against the Simultaneous Iterative Reconstruction Technique (SIRT), POCS-TV, and POCS-RTV algorithms. The evaluation involved two stages: a simulation experiment using a Shepp-Logan phantom with added Poisson-Gaussian noise to mimic low-SNR conditions, and a physical experiment using a 70 mm diameter high-strength steel wire rope phantom scanned by a 9 MeV Rhodotron accelerator CT system.
Results
In the simulation experiment, the POCS-BTV algorithm demonstrated superior quantitative performance, achieving a Peak Signal-to-Noise Ratio (PSNR) of 30.76 and a Structural Similarity Index (SSIM) of 0.8405, which were significantly better than the comparison algorithms. In the real data experiment, visual analysis of the reconstructed images showed that POCS-BTV successfully resolved the fine gaps between individual steel wires. This was in stark contrast to other methods, which suffered from structural aliasing and blurred edges due to noise.
Conclusions
The POCS-BTV algorithm effectively unlocks the high-resolution potential of the Rhodotron accelerator hardware, even in challenging low-SNR scenarios. By achieving an optimal balance between noise suppression and detail preservation, it provides a robust and reliable solution for the precision NDT of critical high-density industrial components, demonstrating significant value for practical engineering applications.
- Rhodotron accelerator /
- Industrial computed tomography /
- CT image reconstruction /
- Bilateral total variation /
- Non-destructive testing

HTML全文

图 1 Rhodotron加速器示意图

Figure 1. Schematic diagram of the Rhodotron accelerator

下载: 全尺寸图片幻灯片

图 2 RTV和BTV对图像结构边缘影响对比

Figure 2. Comparison of the impact of RTV and BTV on image structural edges

下载: 全尺寸图片幻灯片

图 3 Shepp-Logan头模原始图像与各算法重建图像

Figure 3. Shepp-Logan head mode original image and each algorithm reconstruction image

下载: 全尺寸图片幻灯片

图 4 不同算法重建图像的灰度变化曲线

Figure 4. Gray-scale change curves of images reconstructed by different algorithms

下载: 全尺寸图片幻灯片

图 5 高强度钢丝缆绳模体实物图

Figure 5. Physical image of high strength steel wire cable mold

下载: 全尺寸图片幻灯片

图 6 不同重建算法的CT图像及其ROI图像

Figure 6. CT images and ROI images of different reconstruction algorithms

下载: 全尺寸图片幻灯片

图 7 Rhodotron加速器与常规电子直线加速器的CT重建结果对比

Figure 7. Comparison of CT reconstruction results between the Rhodotron accelerator and a conventional electron linear accelerator

下载: 全尺寸图片幻灯片

表 1 POCS-BTV重建算法主要步骤

Table 1. The main steps of the POCS-BTV reconstruction algorithm

No.	main steps	detailed process
①	set initial reconstruction parameters	Projection data g, initial value of reconstructed image ${{\boldsymbol{f}}^{\left( 0 \right)}}$, number of iterations ${N_{{\mathrm{iteration}}}}$, number of BTV iterations ${N_{{\mathrm{BTV}}}}$, number of BTV inner iterations t_max, stability parameter $ \zeta $, regularization parameter $\lambda $, spatial weighting parameter ${\delta _k}$, intensity weighting parameter ${\delta _r}$.
②	POCS reconstruction	Obtain intermediate image ${{\boldsymbol{f}}^{\left( {n + {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}} \right)}}$ using Eq. (10) based on projection data and current initial iteration value.
③	BTV regularization	Apply regularization constraints to intermediate image ${{\boldsymbol{f}}^{\left( {n + {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}} \right)}}$ using Eq. (16) to obtain reconstructed image $ {{\boldsymbol{f}}^{\left( {n + 1} \right)}} $.
④	termination check	If stopping criteria are satisfied (reaching maximum iterations ${N_{{\mathrm{BTV}}}}$), output reconstructed image $ {{\boldsymbol{f}}^{\left( {n + 1} \right)}} $; Otherwise, set result as new initial value and continue iteration.

下载: 导出CSV

表 2 Rhodotron加速器CT仿真扫描参数

Table 2. CT simulation scanning parameters of the Rhodotron accelerator

distance from radiation source to rotation center/mm	distance from radiation source to detector/mm	number of scanning divisions	number of detector units	detector pixel width/mm
75	1800	1200	2000	0.139

下载: 导出CSV

表 3 不同重建算法的定量评价指标结果

Table 3. Quantitative evaluation index results of different reconstruction algorithms

algorithms	PSNR↑	SSIM↑	NMSE↓	FSIM↑
SIRT	20.68	0.1121	0.0758	0.6391
POCS-TV	28.87	0.6788	0.0115	0.9565
POCS-RTV	28.97	0.7958	0.0112	0.9715
POCS-BTV	30.76	0.8405	0.0074	0.9707

下载: 导出CSV

表 4 高强度钢丝缆绳模体的Rhodotron加速器CT扫描参数

Table 4. CT scanning parameters of high strength steel wire cable mold by Rhodotron accelerator

number of scanning divisions	distance from radiation source to rotation center/mm	distance from radiation source to detector/mm	number of detector units	detector pixel width/mm
1200	985	3940	4256	0.139

下载: 导出CSV

参考文献(22)

[1]	Withers P J, Bouman C, Carmignato S, et al. X-ray computed tomography[J]. Nature Reviews Methods Primers, 2021, 1: 18. doi: 10.1038/s43586-021-00015-4
[2]	He Xiaozhong, Liao Shuqing, Long Jidong, et al. A proposal of using improved Rhodotron as a high dose rate micro-focused X-ray source[C]//Proceedings of the 13th Symposium on Accelerator Physics (SAP 17). 2017: 28-30.
[3]	He Xiaozhong, Yang Liu, Liao Shuqing, et al. Rhodotron and rotating target: a solution towards micro-spot for high energy and high dose rate bremsstrahlung sources[J]. Applied Radiation and Isotopes, 2022, 189: 110446. doi: 10.1016/j.apradiso.2022.110446
[4]	Balda M, Hornegger J, Heismann B. Ray contribution masks for structure adaptive sinogram filtering[J]. IEEE Transactions on Medical Imaging, 2012, 31(6): 1228-1239. doi: 10.1109/TMI.2012.2187213
[5]	Xie Q, Zeng D, Zhao Q, et al. Robust low-dose CT sinogram preprocessing via exploiting noise-generating mechanism[J]. IEEE Transactions on Medical Imaging, 2017, 36(12): 2487-2498. doi: 10.1109/TMI.2017.2767290
[6]	Gui Zhiguo, Liu Yi. Noise reduction for low-dose X-ray computed tomography with fuzzy filter[J]. Optik, 2012, 123(13): 1207-1211. doi: 10.1016/j.ijleo.2011.07.052
[7]	蔡玉芳, 陈桃艳, 王珏, 等. 基于自适应滤波系数的非局部均值计算机层析成像的图像降噪方法[J]. 光学学报, 2020, 40: 071001 Cai Yufang, Chen Taoyan, Wang Jue, et al. Image noise reduction in computed tomography with non-local means algorithm based on adaptive filtering coefficients[J]. Acta Optica Sinica, 2020, 40: 071001
[8]	龙超, 金恒, 黎玲, 等. 基于特征融合的非局部均值CT图像降噪[J]. 光学学报, 2022, 42: 1134024 doi: 10.3788/AOS202242.1134024 Long Chao, Jin Heng, Li Ling, et al. CT image denoising with non-local means based on feature fusion[J]. Acta Optica Sinica, 2022, 42: 1134024 doi: 10.3788/AOS202242.1134024
[9]	Dabov K, Foi A, Katkovnik V, et al. Image denoising by sparse 3-D transform-domain collaborative filtering[J]. IEEE Transactions on Image Processing, 2007, 16(8): 2080-2095. doi: 10.1109/TIP.2007.901238
[10]	Zhong Hua, Ma Ke, Zhou Yang. Modified BM3D algorithm for image denoising using nonlocal centralization prior[J]. Signal Processing, 2015, 106: 342-347. doi: 10.1016/j.sigpro.2014.08.014
[11]	Sidky E Y, Pan Xiaochuan. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization[J]. Physics in Medicine & Biology, 2008, 53(17): 4777-4807.
[12]	Sidky E Y, Duchin Y, Pan Xiaochuan, et al. A constrained, total-variation minimization algorithm for low-intensity X-ray CT[J]. Medical Physics, 2011, 38(S1): S117-S125. doi: 10.1118/1.3560887
[13]	Xu Li, Yan Qiong, Xia Yan, et al. Structure extraction from texture via relative total variation[J]. ACM Transactions on Graphics, 2012, 31: 139.
[14]	Gong Changcheng, Zeng Li. Adaptive iterative reconstruction based on relative total variation for low-intensity computed tomography[J]. Signal Processing, 2019, 165: 149-162. doi: 10.1016/j.sigpro.2019.06.031
[15]	He Lei, Xie Yongfang, Xie Shiwen, et al. Structure-preserving texture smoothing via scale-aware bilateral total variation[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2023, 33(4): 1493-1506. doi: 10.1109/TCSVT.2022.3214219
[16]	Chen Hongchi, Li Qiuxia, Zhou Lazhen, et al. Deep learning-based algorithms for low-dose CT imaging: a review[J]. European Journal of Radiology, 2024, 172: 111355. doi: 10.1016/j.ejrad.2024.111355
[17]	Ma Limin, Yao Yudong, Teng Yueyang. Iterator-net: sinogram-based CT image reconstruction[J]. Mathematical Biosciences and Engineering, 2022, 19(12): 13050-13061. doi: 10.3934/mbe.2022609
[18]	Combettes P L, Wajs V R. Signal recovery by proximal forward-backward splitting[J]. Multiscale Modeling & Simulation, 2005, 4(4): 1168-1200.
[19]	Hale E T, Yin Wotao, Zhang Yin. Fixed-point continuation for ℓ₁-minimization: methodology and convergence[J]. SIAM Journal on Optimization, 2008, 19(3): 1107-1130. doi: 10.1137/070698920
[20]	Tian Zhen, Jia Xun, Yuan Kehong, et al. Low-dose CT reconstruction via edge-preserving total variation regularization[J]. Physics in Medicine & Biology, 2011, 56(18): 5949-5967.
[21]	Krishnan D, Szeliski R. Multigrid and multilevel preconditioners for computational photography[J]. ACM Transactions on Graphics (TOG), 2011, 30(6): 1-10.
[22]	Liu Yan, Ma Jianhua, Fan Yi, et al. Adaptive-weighted total variation minimization for sparse data toward low-dose x-ray computed tomography image reconstruction[J]. Physics in Medicine & Biology, 2012, 57(23): 7923-7956.