High-precision control of nanoparticles using fractional-order vortex laser beams
-
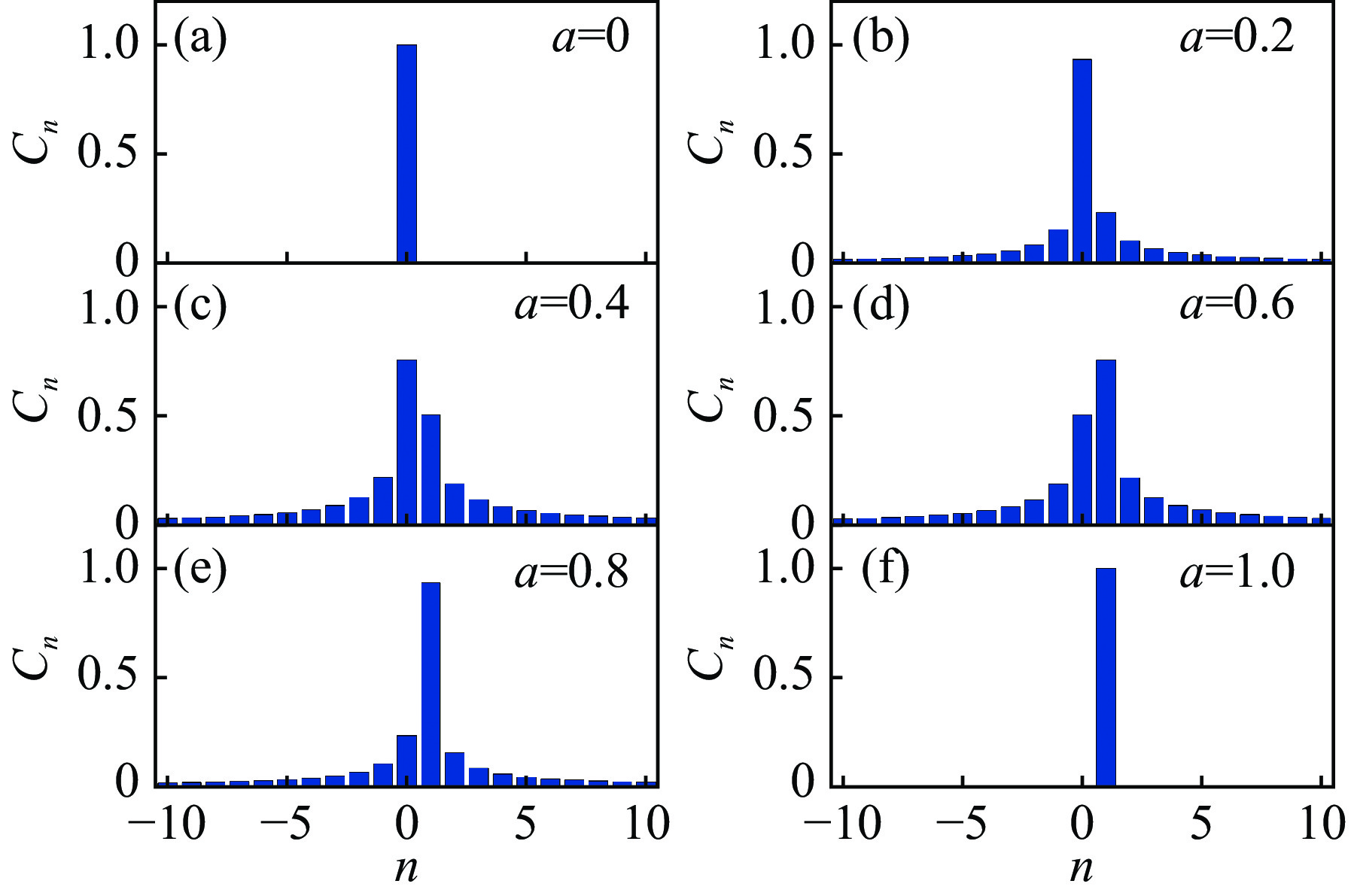
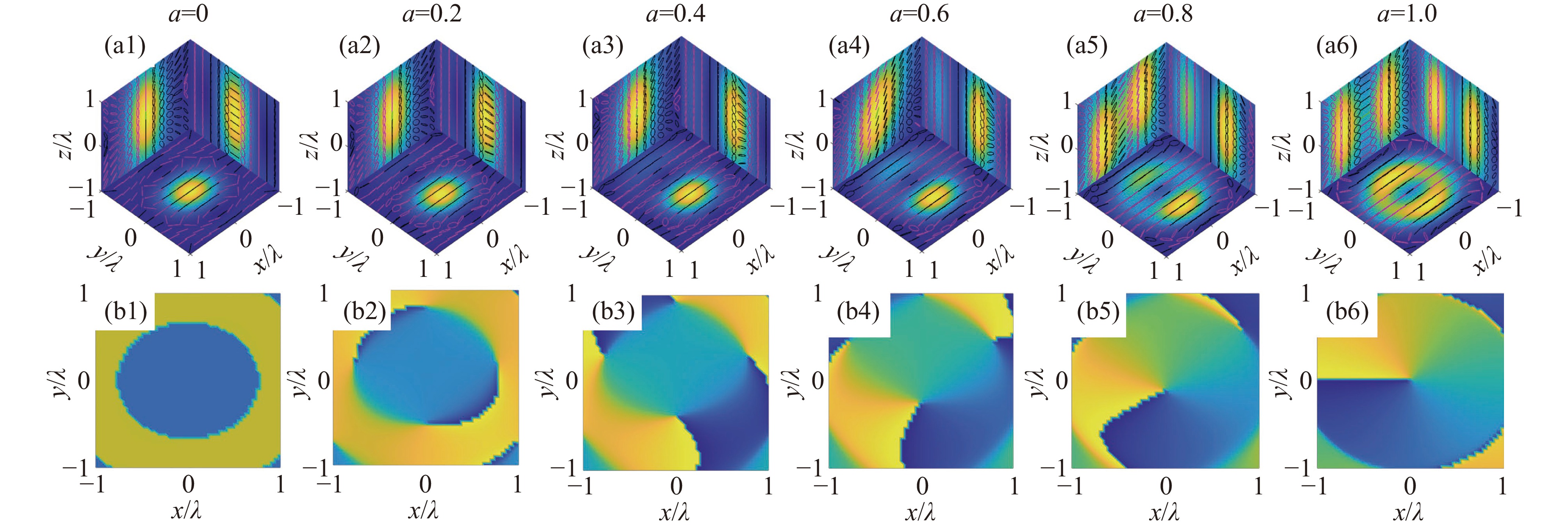
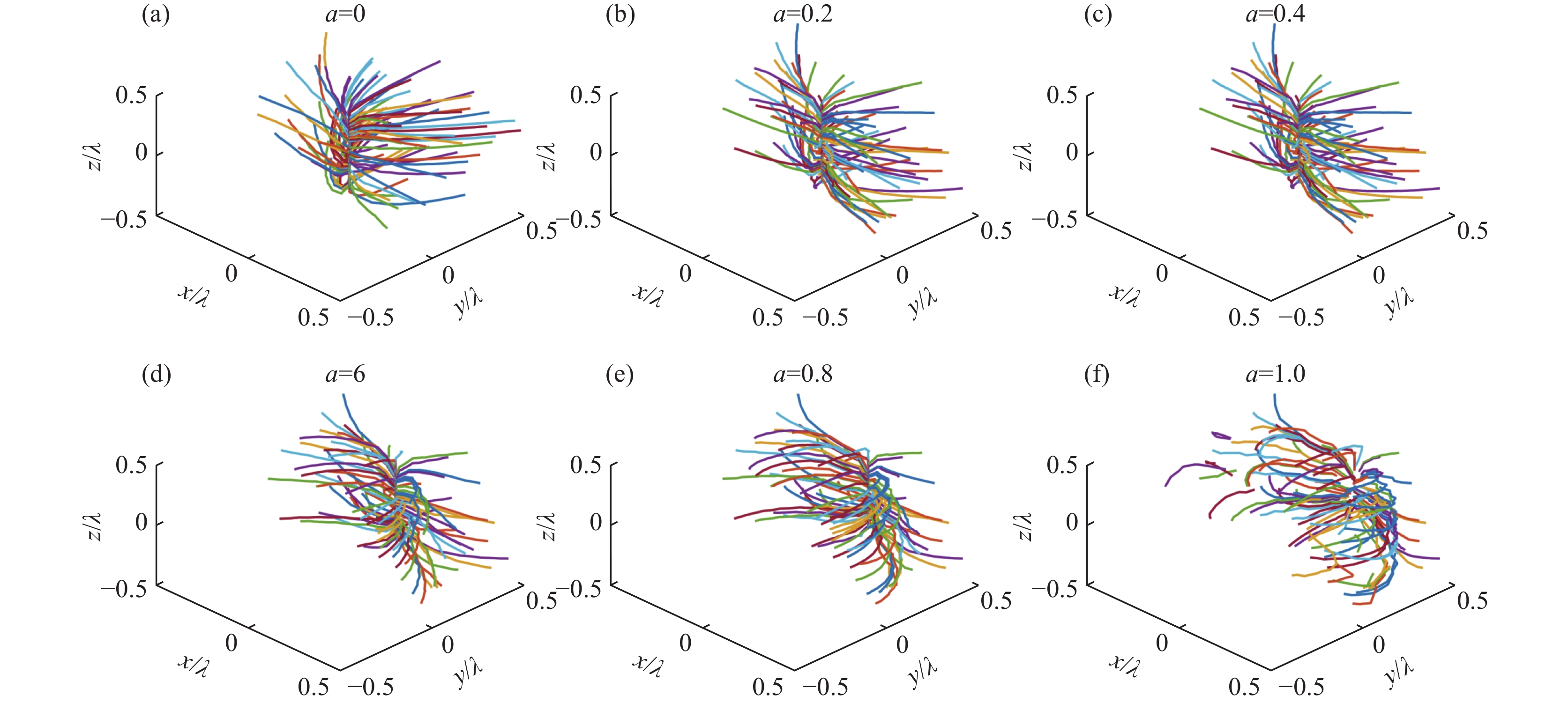
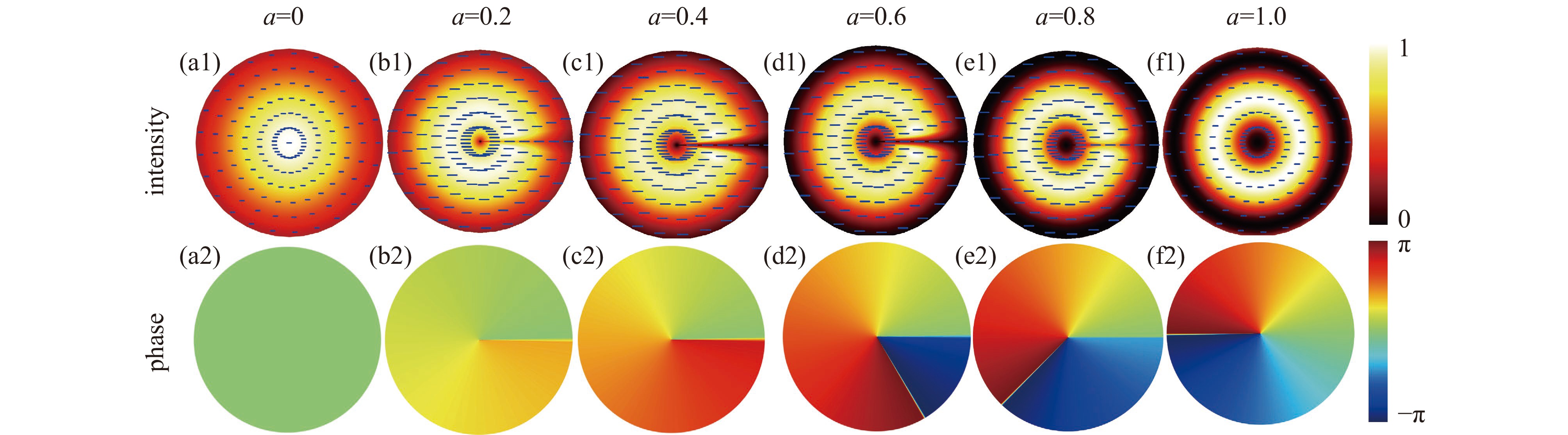
摘要: 提出了一种基于分数阶涡旋光束的纳米粒子三维操控方法。通过建立分数阶涡旋光束的矢量衍射模型，揭示了拓扑系数与光场相位奇异性之间的映射关系。数值模拟结果表明，分数阶涡旋光束的焦场可视为整数阶模式的相干叠加，且其权重分布呈现显著的非对称特性。此外，还建立了基于分数阶涡旋光束捕获纳米粒子的光力模型。研究表明，通过调节分数阶涡旋光束的拓扑系数，可以实现对球形纳米粒子的精确操控。粒子在横向平面上的捕获位置与拓扑系数之间呈线性依赖关系。与传统的整数阶光束相比，该方法通过连续调节拓扑系数，实现了横向捕获位置的精确连续调控。理论计算与Langevin动力学模拟的结果进一步验证了该技术在三维空间内能够实现纳米粒子的多自由度协同操控。Abstract:
Background Optical manipulation based on integer-order vortex beams is widely used in nanotechnology, yet their discrete nature restricts continuous and precise transverse control of nanoparticles.Purpose This study aims to overcome this limitation by proposing a novel approach using fractional-order vortex beams (FVBs), with the goal of achieving continuous and precise transverse optical trapping and manipulation of nanoparticles.Methods We developed a vector diffraction model to characterize the focal field of FVBs, revealing it as a coherent superposition of integer-order modes with a highly asymmetric weight distribution. Additionally, an optical force model was established to analyze the trapping behavior of spherical nanoparticles. Theoretical calculations and Langevin dynamics simulations were employed to evaluate the three-dimensional trapping stability and multi-degree-of-freedom manipulation capability.Results The transverse trapping position exhibits a linear dependence on the fractional topological charge. By continuously tuning the topological charge, nanoparticles can be displaced precisely and continuously in the transverse plane with sub-wavelength accuracy—a capability not achievable with conventional integer-order vortex beams. Simulations further confirm the stability of the three-dimensional trap and the feasibility of coordinated multi-degree-of-freedom manipulation.Conclusions This work demonstrates that fractional-order vortex beams offer a superior alternative for high-precision optical manipulation. They provide a powerful and novel technique for applications in microfluidics, nanofabrication, and lab-on-a-chip devices. -
图 1 具有不同拓扑系数的线偏振涡旋光束的入射光强、偏振态以及相位分布情况
Figure 1. The incident intensity, polarization state, and phase distributions of linearly polarized vortex beams with different topological charges
图 2 具有不同拓扑系数的分数阶线偏振涡旋光束与整数阶涡旋光束的关系图
Figure 2. The diagram illustrating the relationship between fractional-order linearly polarized vortex beams and integer-order vortex beams
图 3 紧聚焦的分数阶线偏振涡旋光束在焦场范围内的归一化强度、偏振态的三维投影及相位分布情况
Figure 3. (a)The normalized intensity, three-dimensional polarization projections, and (b) phase distribution of tightly focused fractional-order linearly polarized vortex beams within the focal region
图 4 紧聚焦的分数阶线偏振涡旋光束捕获球形纳米粒子时，粒子在焦场范围内受到的光力分布(a)Fxy、(b)Fxz和(c)Fyz
Figure 4. The optical force distributions experienced by spherical nanoparticles captured by tightly focused fractional-order linearly polarized vortex beams within the focal region: (a)Fxy、(b)Fxz和(c)Fyz
图 5 分数阶线偏振涡旋光束捕获球形纳米粒子时，粒子在三维焦场中的运动轨迹
Figure 5. The trajectory of spherical nanoparticles within the three-dimensional focal field when captured by fractional-order linearly polarized vortex beams
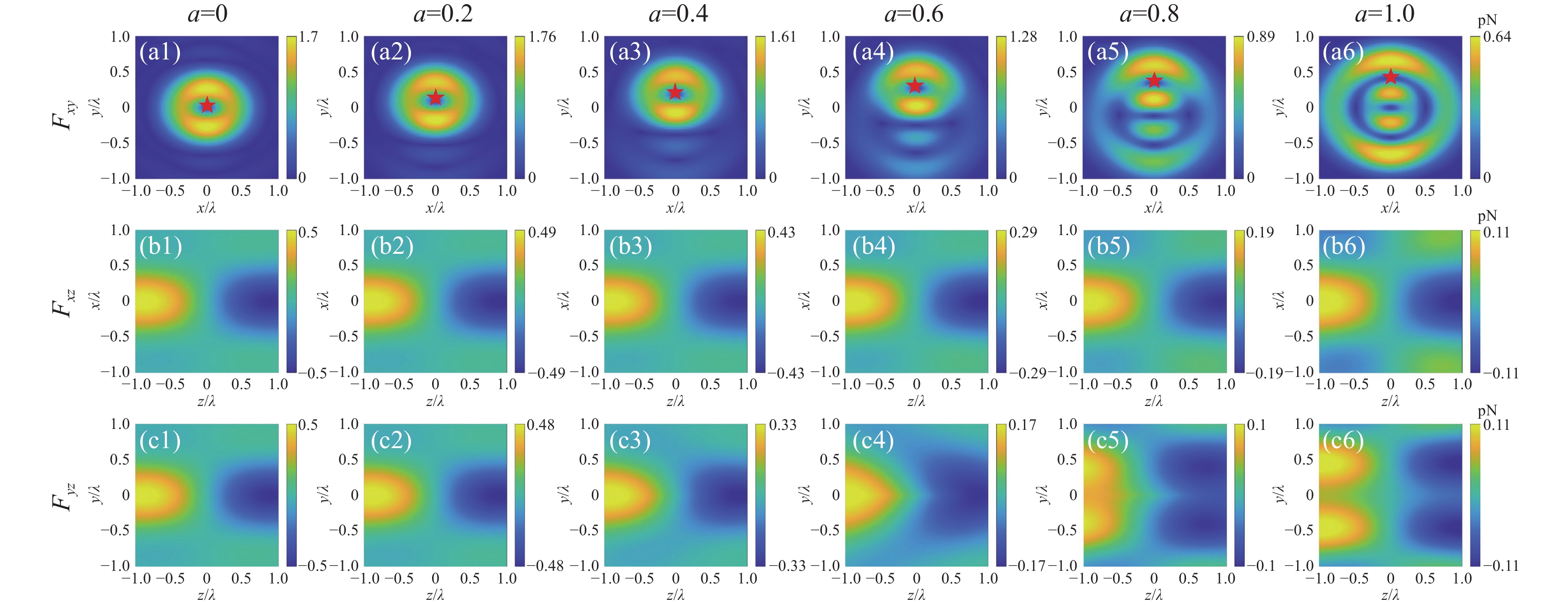
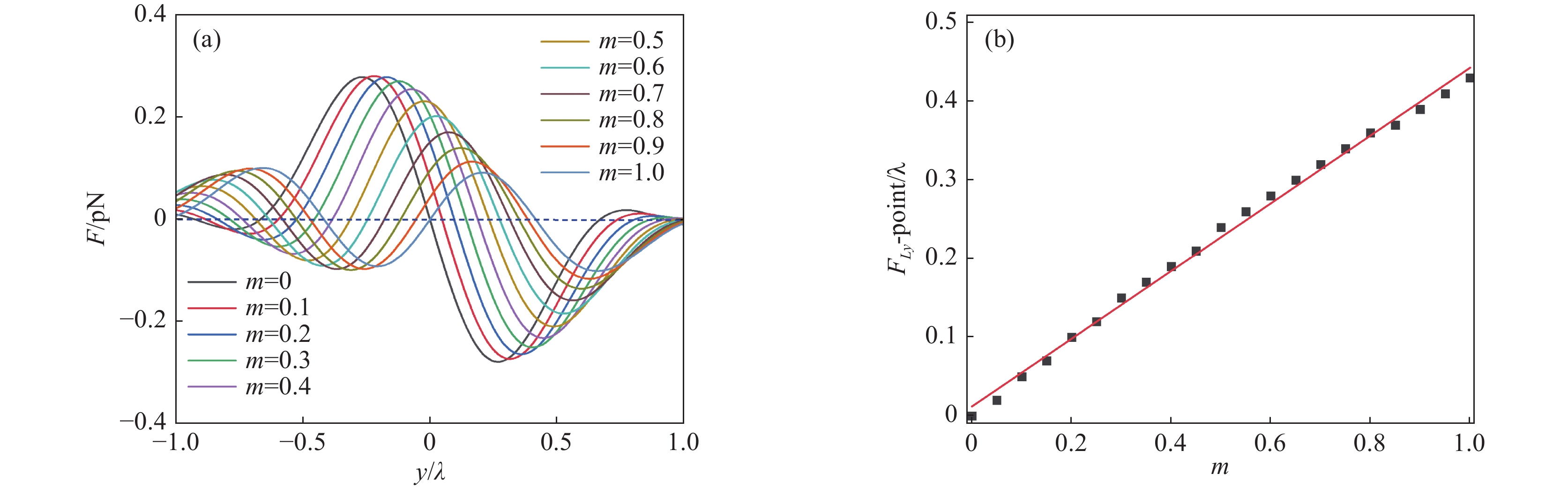
图 6 分数阶线偏振涡旋光束捕获球形纳米粒子时，粒子在y方向上的(a)横向光力和(b)稳定捕获位置与拓扑系数a之间的依赖关系
Figure 6. The dependence of (a) the lateral optical force in the y-direction and (b) the stable trapping position on the topological coefficient a when spherical nanoparticles are captured by fractional-order linearly polarized vortex beams
-
[1] Stoev I D, Seelbinder B, Erben E, et al. Highly sensitive force measurements in an optically generated, harmonic hydrodynamic trap[J]. eLight, 2021, 1(1): 7. doi: 10.1186/s43593-021-00007-7 [2] Ashkin A, Dziedzic J M, Bjorkholm J E, et al. Observation of a single-beam gradient force optical trap for dielectric particles[J]. Optics Letters, 1986, 11(5): 288-290. doi: 10.1364/OL.11.000288 [3] Obrzud E, Rainer M, Harutyunyan A, et al. A microphotonic astrocomb[J]. Nature Photonics, 2019, 13(1): 31-35. doi: 10.1038/s41566-018-0309-y [4] 童唯扬, 王正岭. 考虑光镊效应的飞秒激光双光子加工线宽[J]. 强激光与粒子束, 2018, 30(3): 034102Tong Weiyang, Wang Zhengling. Linewidth of femtosecond laser two-photon processing considering optical tweezers[J]. High Power Laser and Particle Beams, 2018, 30(3): 034102 [5] Zhu Runlin, Shen Tianci, Gu Zhaoqi, et al. Amphibious hybrid laser tweezers for fluid and solid domains[J]. ACS Nano, 2024, 18(34): 23232-23242. doi: 10.1021/acsnano.4c05970 [6] Ji Zhaoqi, Jiang Chunlei, Chen Peng, et al. Radial rotation of cell-pair under beam mode coupling effect of microcavity cascaded single fiber optical tweezers[J]. Nanophotonics, 2025, 14(9): 1405-1414. doi: 10.1515/nanoph-2025-0033 [7] Sneh T, Corsetti S, Notaros M, et al. Optical tweezing of microparticles and cells using silicon-photonics-based optical phased arrays[J]. Nature Communications, 2024, 15(1): 8493. doi: 10.1038/s41467-024-52273-x [8] Kabi S, Alinezhad H G, Langari A, et al. Impact of a laser magnetic field on optical trapping[J]. Optica, 2024, 11(9): 1295-1302. doi: 10.1364/OPTICA.528850 [9] Peng Miao, Xiao Guangzong, Chen Xinlin, et al. Optical trapping-enhanced probes designed by a deep learning approach[J]. Photonics Research, 2024, 12(5): 959-968. doi: 10.1364/PRJ.517547 [10] Lee J, Arita Y, Toyoshima S, et al. Photopolymerization with light fields possessing orbital angular momentum: generation of helical microfibers[J]. ACS Photonics, 2018, 5(10): 4156-4163. doi: 10.1021/acsphotonics.8b00959 [11] Terno D R. Two roles of relativistic spin operators[J]. Physical Review A, 2003, 67(1): 014102. [12] Zhang Xiaohe, Rui Guanghao, He Jun, et al. Nonlinear accelerated orbiting motions of optical trapped particles through two-photon absorption[J]. Optics Letters, 2021, 46(1): 110-113. doi: 10.1364/OL.411216 [13] Brunet C, Rusch L A. Optical fibers for the transmission of orbital angular momentum modes[J]. Optical Fiber Technology, 2017, 35: 2-7. doi: 10.1016/j.yofte.2016.09.016 [14] Toyoda K, Miyamoto K, Aoki N, et al. Using optical vortex to control the chirality of twisted metal nanostructures[J]. Nano Letters, 2012, 12(7): 3645-3649. doi: 10.1021/nl301347j [15] Gu Liangliang, Cao Qian, Zhan Qiwen. Spatiotemporal optical vortex wavepackets with phase singularities embedded in multiple domains [Invited][J]. Chinese Optics Letters, 2023, 21(8): 080003. doi: 10.3788/COL202321.080003 [16] Shahabadi V, Abdollahpour D. Dual-plane multiple-trapping by tightly focused petal-like circular Airy beam in an aqueous medium[J]. Journal of Quantitative Spectroscopy & Radiative Transfer, 2021, 272: 107771. [17] Chen Y F, Huang K F, Lai H C, et al. Observation of vector vortex lattices in polarization states of an isotropic microcavity laser[J]. Physical Review Letters, 2003, 90(5): 053904. doi: 10.1103/PhysRevLett.90.053904 [18] Berry M V. Optical vortices evolving from helicoidal integer and fractional phase steps[J]. Journal of Optics A: Pure and Applied Optics, 2004, 6(2): 259-268. doi: 10.1088/1464-4258/6/2/018 [19] Leach J, Yao E, Padgett M J. Observation of the vortex structure of a non-integer vortex beam[J]. New Journal of Physics, 2004, 6: 71. doi: 10.1088/1367-2630/6/1/071 [20] Alperin S N, Siemens M F. Angular momentum of topologically structured darkness[J]. Physical Review Letters, 2017, 119(20): 203902. doi: 10.1103/PhysRevLett.119.203902 [21] Tkachenko G, Chen Mingzhou, Dholakia K, et al. Is it possible to create a perfect fractional vortex beam?[J]. Optica, 2017, 4(3): 330-333. doi: 10.1364/OPTICA.4.000330 [22] Richards B, Wolf E. Electromagnetic diffraction in optical system. II. Structure of the image field in an aplanatic system[J]. Proceedings of the Royal Society A: Mathematical, Physical & Engineering Sciences, 1959, 253(1274): 358-379. [23] Youngworth K S, Brown T G. Focusing of high numerical aperture cylindrical-vector beams[J]. Optics Express, 2000, 7(2): 77-87. doi: 10.1364/OE.7.000077 [24] Gu Bing, Cui Yiping. Nonparaxial and paraxial focusing of azimuthal-variant vector beams[J]. Optics Express, 2012, 20(16): 17684-17694. doi: 10.1364/OE.20.017684 [25] Chaumet P C, Nieto-Vesperinas M. Time-averaged total force on a dipolar sphere in an electromagnetic field[J]. Optics Letters, 2000, 25(15): 1065-1067. doi: 10.1364/OL.25.001065 [26] Guo Min, Wu Yicong, Hobson C M, et al. Deep learning-based aberration compensation improves contrast and resolution in fluorescence microscopy[J]. Nature Communications, 2025, 16(1): 313. doi: 10.1038/s41467-024-55267-x [27] Sule N, Rice S A, Gray S K, et al. An electrodynamics-Langevin dynamics (ED-LD) approach to simulate metal nanoparticle interactions and motion[J]. Optics Express, 2015, 23(23): 29978-29992. doi: 10.1364/OE.23.029978 -
下载:
点击查看大图
计量
- 文章访问数: 16
- HTML全文浏览量: 9
- PDF下载量: 2
- 被引次数: 0
