| [1] |
王连杰, 孙伟, 夏榜样, 等. 球床先进高温堆堆芯设计研究[J]. 核动力工程, 2018, 39(s2): 87-91Wang Lianjie, Sun Wei, Xia Bangyang, et al. Research on core design of pebble bed advanced high temperature reactor[J]. Nuclear Power Engineering, 2018, 39(s2): 87-91
|
| [2] |
李睿, 任成, 杨星团, 等. 基于单元体理论的球床堆积结构与传热算法研究[J]. 核动力工程, 2016, 37(3): 39-42Li Rui, Ren Cheng, Yang Xingtuan, et al. Analysis of structures and heat transfer for packed beds[J]. Nuclear Power Engineering, 2016, 37(3): 39-42
|
| [3] |
丁旺. 基于CFD-DEM的颗粒流体两相耦合模型的研究[D]. 上海: 上海交通大学, 2021Ding Wang. Research on the particle-fluid two-phase coupling model based on CFD-DEM[D]. Shanghai: Shanghai Jiao Tong University, 2021
|
| [4] |
苏东升. 基于CFD-DEM耦合模拟方法的水流泥沙运动研究[D]. 天津: 天津大学, 2015Su Dongsheng. Investigation of fluid-sediment particle motion based on CFD-DEM coupling simulation method[D]. Tianjin: Tianjin University, 2015
|
| [5] |
姚鹏, 王远, 冒刘鹏, 等. CFD-DEM模型最优网格尺寸的理论推证[J]. 泥沙研究, 2023, 48(5): 1-7,34Yao Peng, Wang Yuan, Mao Liupeng, et al. Theoretical validation on the optimal mesh size of CFD-DEM model[J]. Journal of Sediment Research, 2023, 48(5): 1-7,34
|
| [6] |
Xie Zhouzun, Wang Shuai, Shen Yansong. A novel hybrid CFD-DEM method for high-fidelity multi-resolution modelling of cross-scale particulate flow[J]. Chemical Engineering Journal, 2023, 455: 140731. doi: 10.1016/j.cej.2022.140731
|
| [7] |
Wang Zekun, Liu Moubin. Semi-resolved CFD-DEM for thermal particulate flows with applications to fluidized beds[J]. International Journal of Heat and Mass Transfer, 2020, 159: 120150. doi: 10.1016/j.ijheatmasstransfer.2020.120150
|
| [8] |
杨星团, 刘志勇, 胡文平, 等. HTR-10堆芯球流运动的唯象学DEM模拟[J]. 原子能科学技术, 2013, 47(12): 2231-2237Yang Xingtuan, Liu Zhiyong, Hu Wenping, et al. DEM simulation of pebble flow in HTR-10 core by phenomenological method[J]. Atomic Energy Science and Technology, 2013, 47(12): 2231-2237
|
| [9] |
徐泳, 孙其诚, 张凌, 等. 颗粒离散元法研究进展[J]. 力学进展, 2003, 33(2): 251-260Xu Yong, Sun Qicheng, Zhang Ling, et al. Advances in discrete element methods for particulate materials[J]. Advances in Mechanics, 2003, 33(2): 251-260
|
| [10] |
Wang Zekun, Teng Yujun, Liu Moubin. A semi-resolved CFD-DEM approach for particulate flows with kernel based approximation and Hilbert curve based searching strategy[J]. Journal of Computational Physics, 2019, 384: 151-169. doi: 10.1016/j.jcp.2019.01.017
|
| [11] |
Pirker S, Kahrimanovic D, Goniva C. Improving the applicability of discrete phase simulations by smoothening their exchange fields[J]. Applied Mathematical Modelling, 2011, 35(5): 2479-2488. doi: 10.1016/j.apm.2010.11.066
|
| [12] |
Rycroft C H. Multiscale modeling in granular flow[D]. Cambridge: Massachusetts Institute of Technology, 2007.
|
| [13] |
严安, 孙喜明, 董玉杰. 球床式高温堆堆芯气固两相流耦合模拟研究[J]. 哈尔滨工程大学学报, 2022, 43(12): 1743-1749Yan An, Sun Ximing, Dong Yujie. Simulation study of gas-solid two-phase flow coupling of pebble-bed cores in a high-temperature reactor[J]. Journal of Harbin Engineering University, 2022, 43(12): 1743-1749
|
| [14] |
蔡国庆, 刁显锋, 杨芮, 等. 基于CFD-DEM的流-固耦合数值建模方法研究进展[J]. 哈尔滨工业大学学报, 2024, 56(1): 17-32Cai Guoqing, Diao Xianfeng, Yang Rui, et al. Research progress of fluid-solid coupling model based on CFD-DEM coupling[J]. Journal of Harbin Institute of Technology, 2024, 56(1): 17-32
|
| [15] |
Suikkanen H, Ritvanen J, Jalali P, et al. Discrete element modelling of pebble packing in pebble bed reactors[J]. Nuclear Engineering and Design, 2014, 273: 24-32. doi: 10.1016/j.nucengdes.2014.02.022
|
| [16] |
王晨洋. 颗粒堆积孔隙结构的统计性质研究[D]. 上海: 华东师范大学, 2024Wang Chenyang. A statistical study of the pore structures of granular packings[D]. Shanghai: East China Normal University, 2024
|
| [17] |
Kloss C, Goniva C, Hager A, et al. Models, algorithms and validation for opensource DEM and CFD–DEM[J]. Progress in Computational Fluid Dynamics, 2012, 12(2/3): 140-152. doi: 10.1504/PCFD.2012.047457
|
| [18] |
Di Felice R. The sedimentation velocity of dilute suspensions of nearly monosized spheres[J]. International Journal of Multiphase Flow, 1999, 25(4): 559-574. doi: 10.1016/S0301-9322(98)00084-6
|
| [19] |
Müller C R, Scott S A, Holland D J, et al. Validation of a discrete element model using magnetic resonance measurements[J]. Particuology, 2009, 7(4): 297-306. doi: 10.1016/j.partic.2009.04.002
|
| [20] |
Zhou Yandaizi, Wang Tielin, Zhu J. Investigation on minimum fluidization velocity in a modified Geldart’s diagram[J]. Chemical Engineering Journal, 2023, 453: 139984. doi: 10.1016/j.cej.2022.139984
|
| [21] |
Wu Hao, Zhao Houjian, Hao Zulong, et al. A non-linear transform approach for conduction-radiation heat transfer in the extended thermal discrete element method[J]. International Journal of Heat and Mass Transfer, 2021, 176: 121432. doi: 10.1016/j.ijheatmasstransfer.2021.121432
|
| [22] |
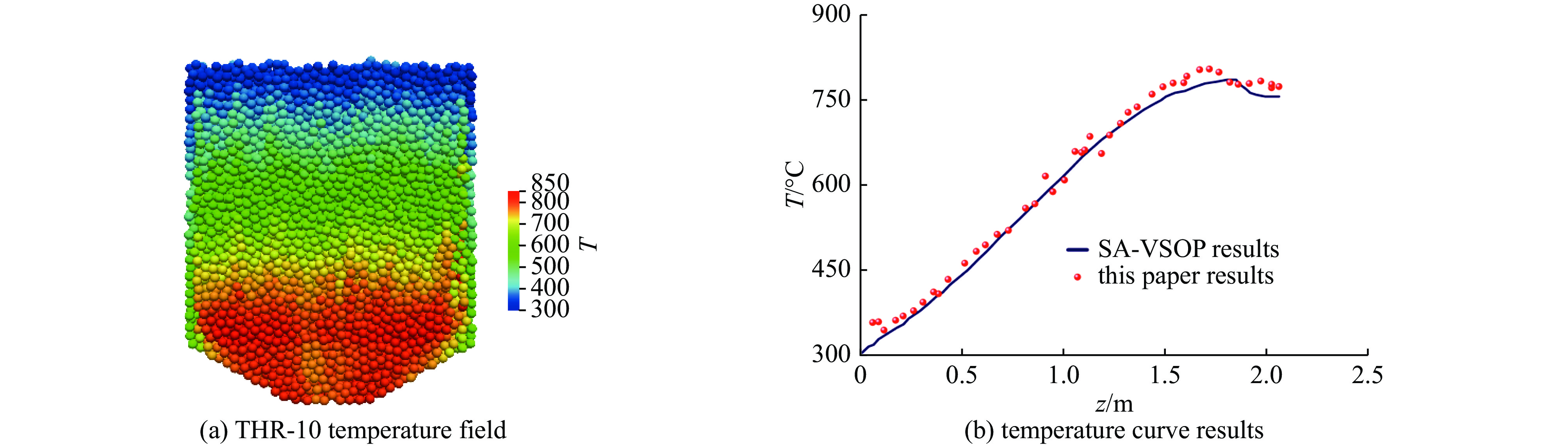
Chen Fubing, Dong Yujie, Zheng Yanhua, et al. Benchmark calculation for the steady-state temperature distribution of the HTR-10 under full-power operation[J]. Journal of Nuclear Science and Technology, 2009, 46(6): 572-580. doi: 10.1080/18811248.2007.9711564
|




 下载:
下载: