-
摘要: 激光器中的反应动力学常包含大量激发态物种。激发态物种之间的相互作用与由此导致的数值刚性是激光器数值模拟的一大挑战。通过神经网络建立激发态反应动力学关系回归可有效降低计算复杂度，为更加准确精细的激光器数值模拟提供可能。但激发态反应动力学的复杂性同样要求神经网络具有较强的回归性能。本研究引入了序列神经网络来在较低参数量的前提下提升网络复杂回归的能力，同时提出了统计网络框架来进一步增加网络输出的多样性。所提出的方法在包含16个物种和137个反应的氟化氢振动态反应机理中进行了验证。在验证过程中，同时发现了随机性对网络性能的影响。Abstract:
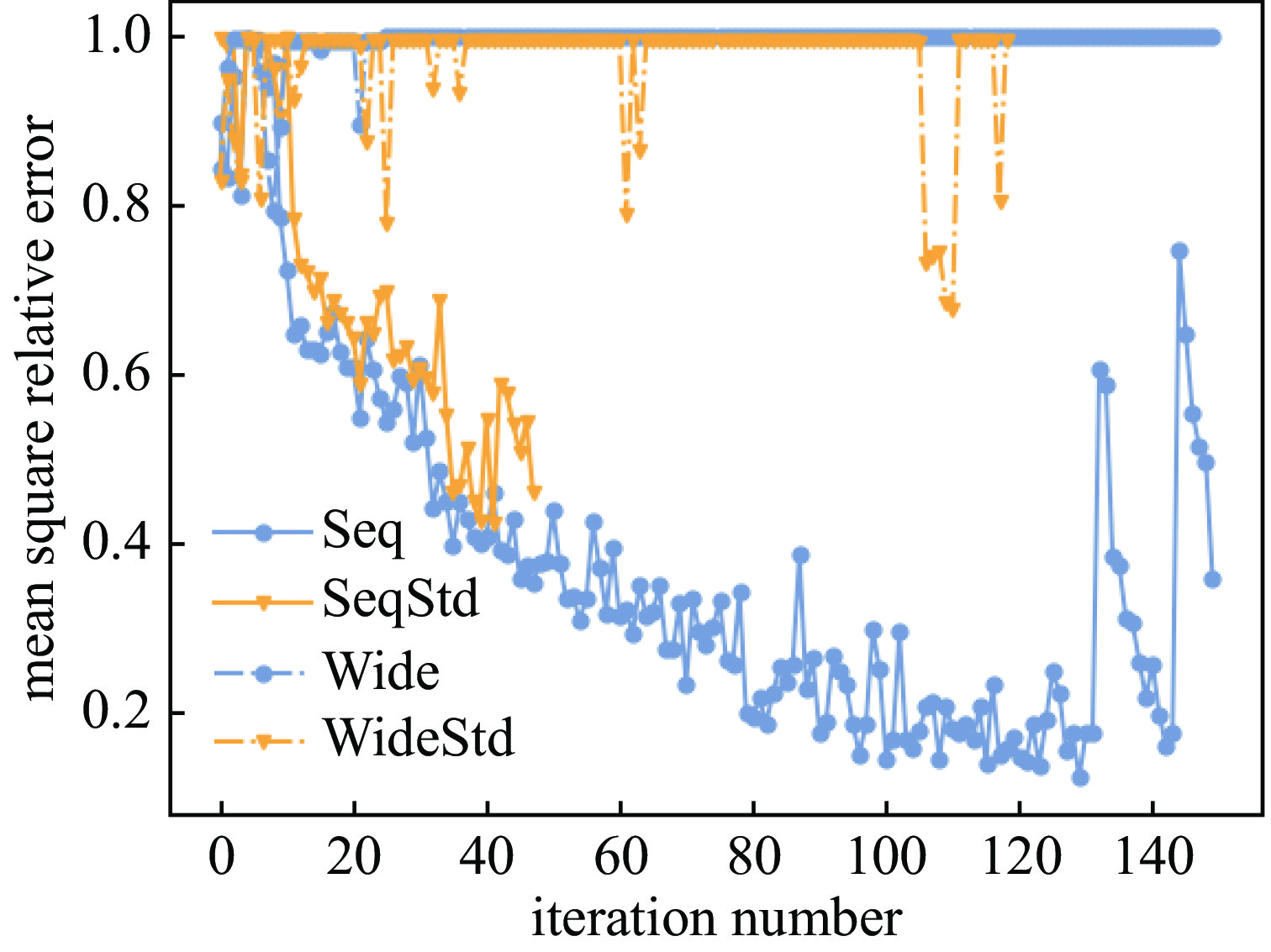
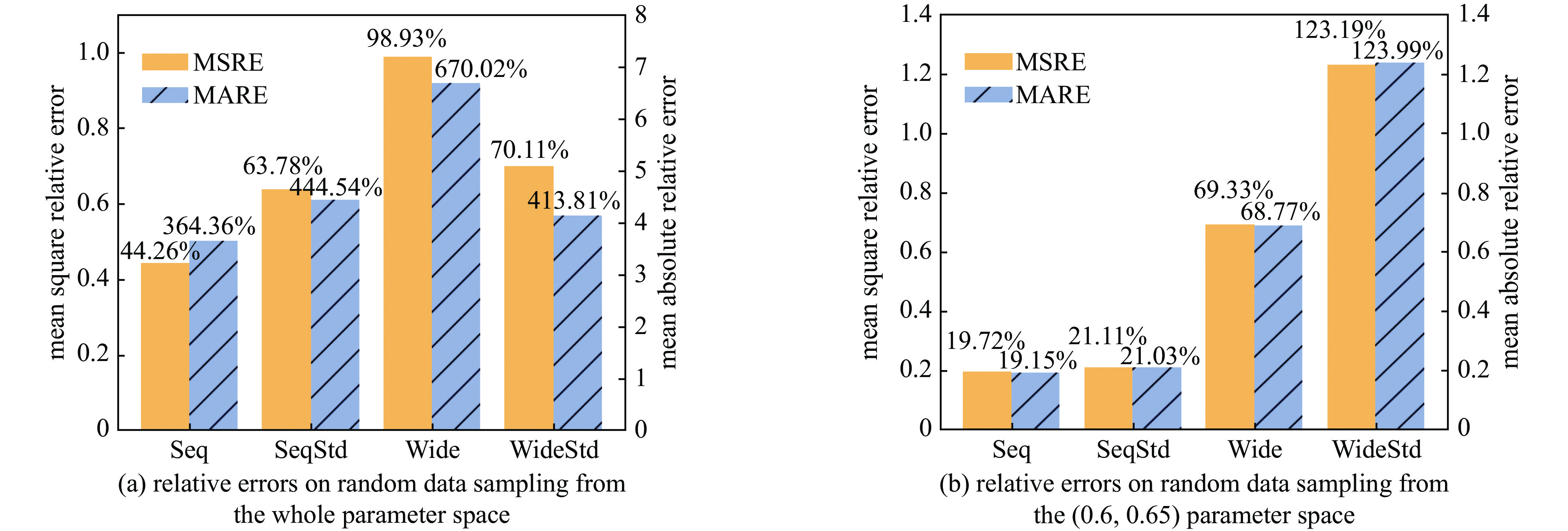
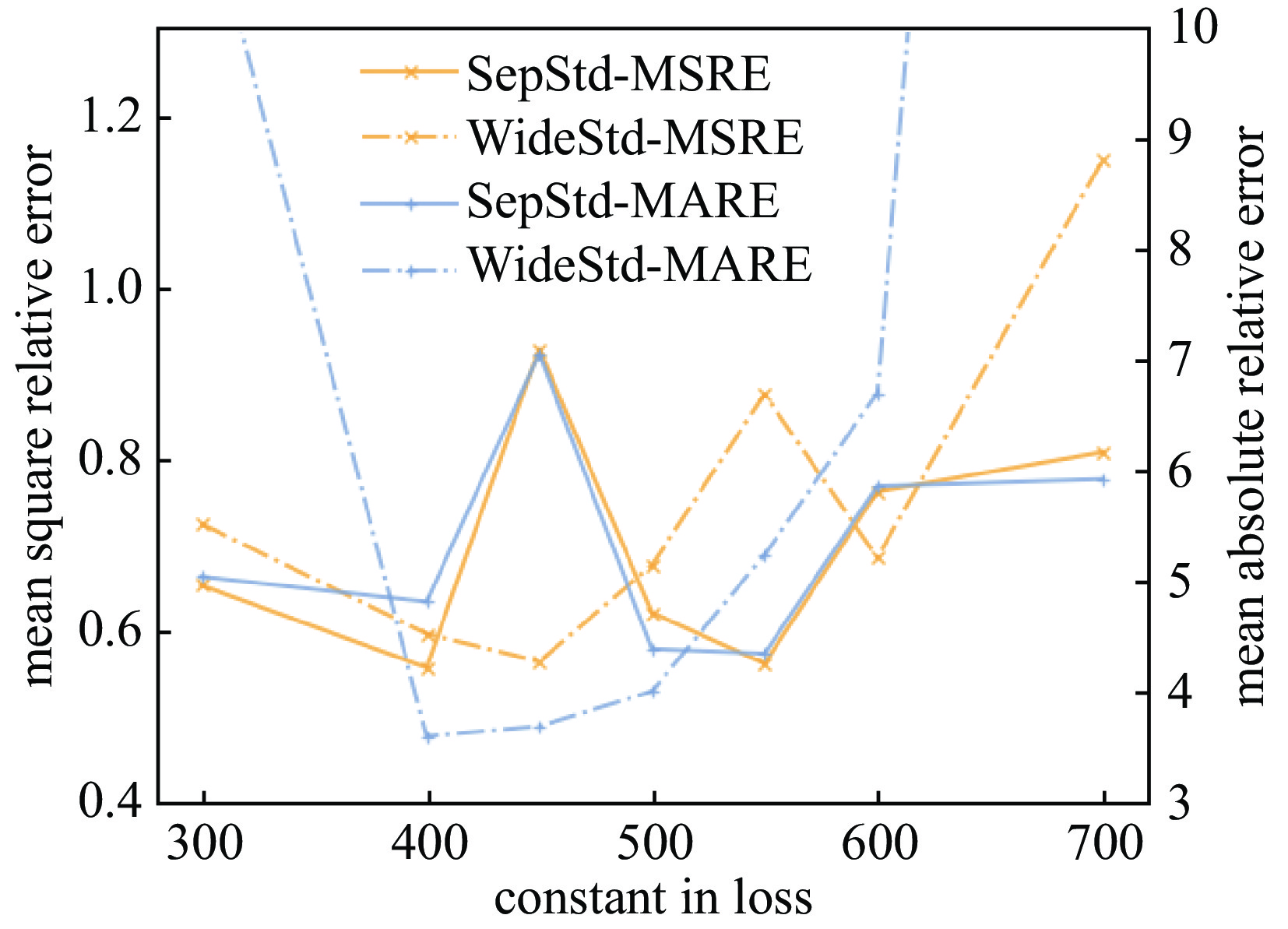
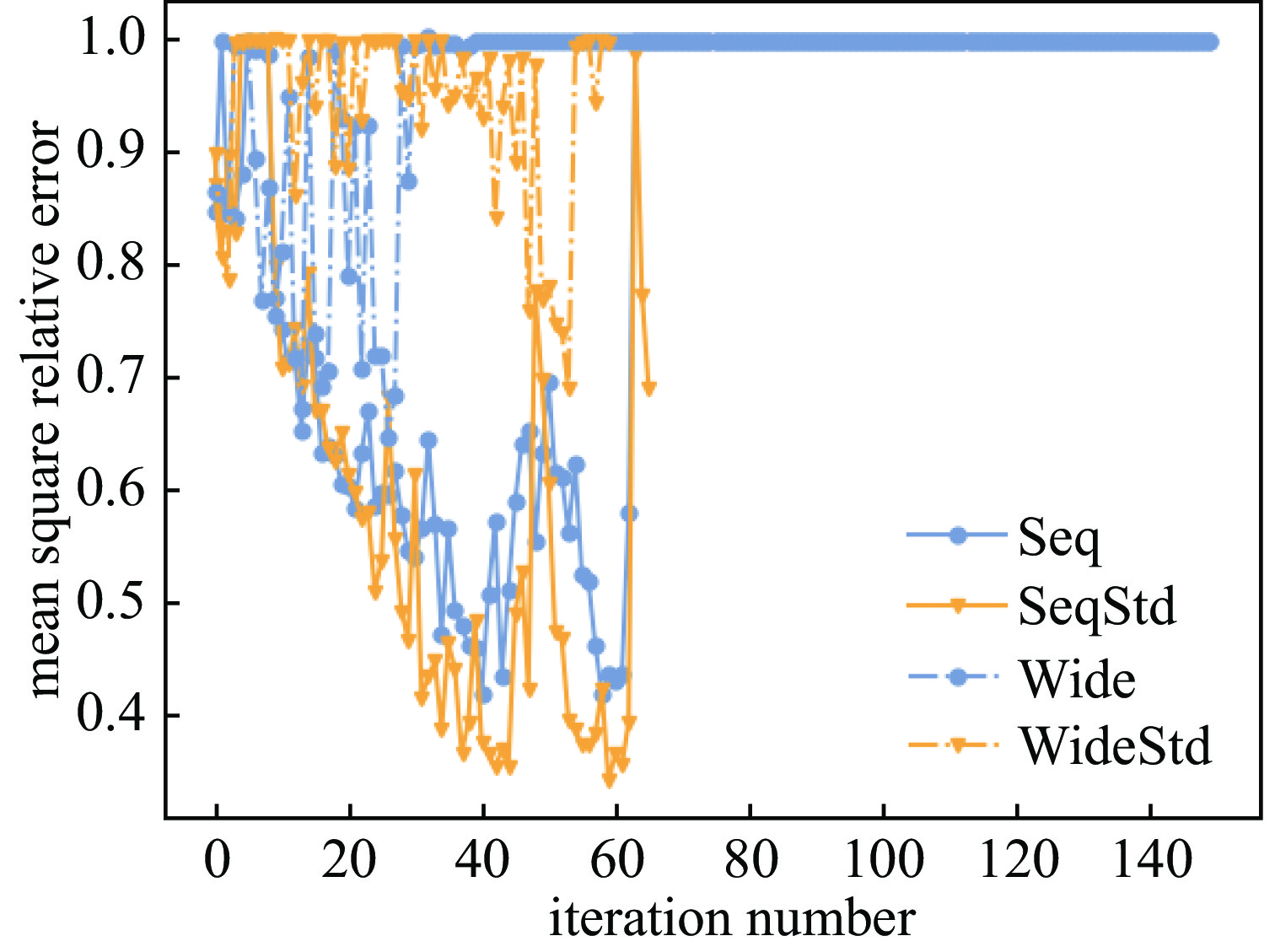
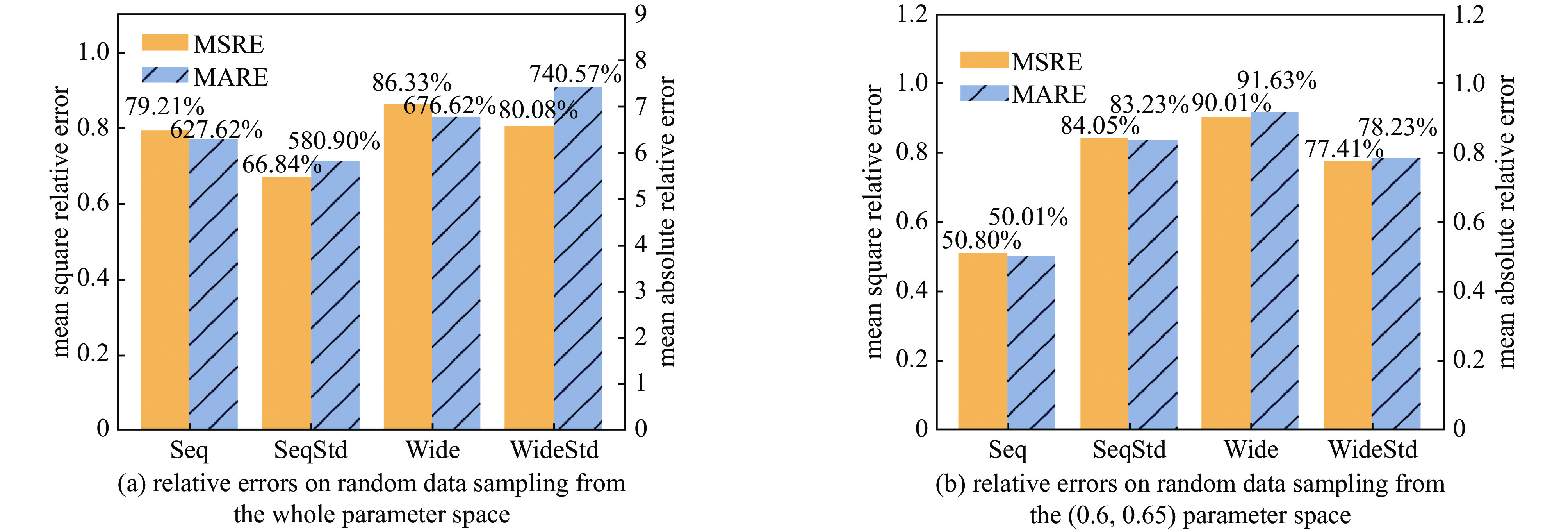
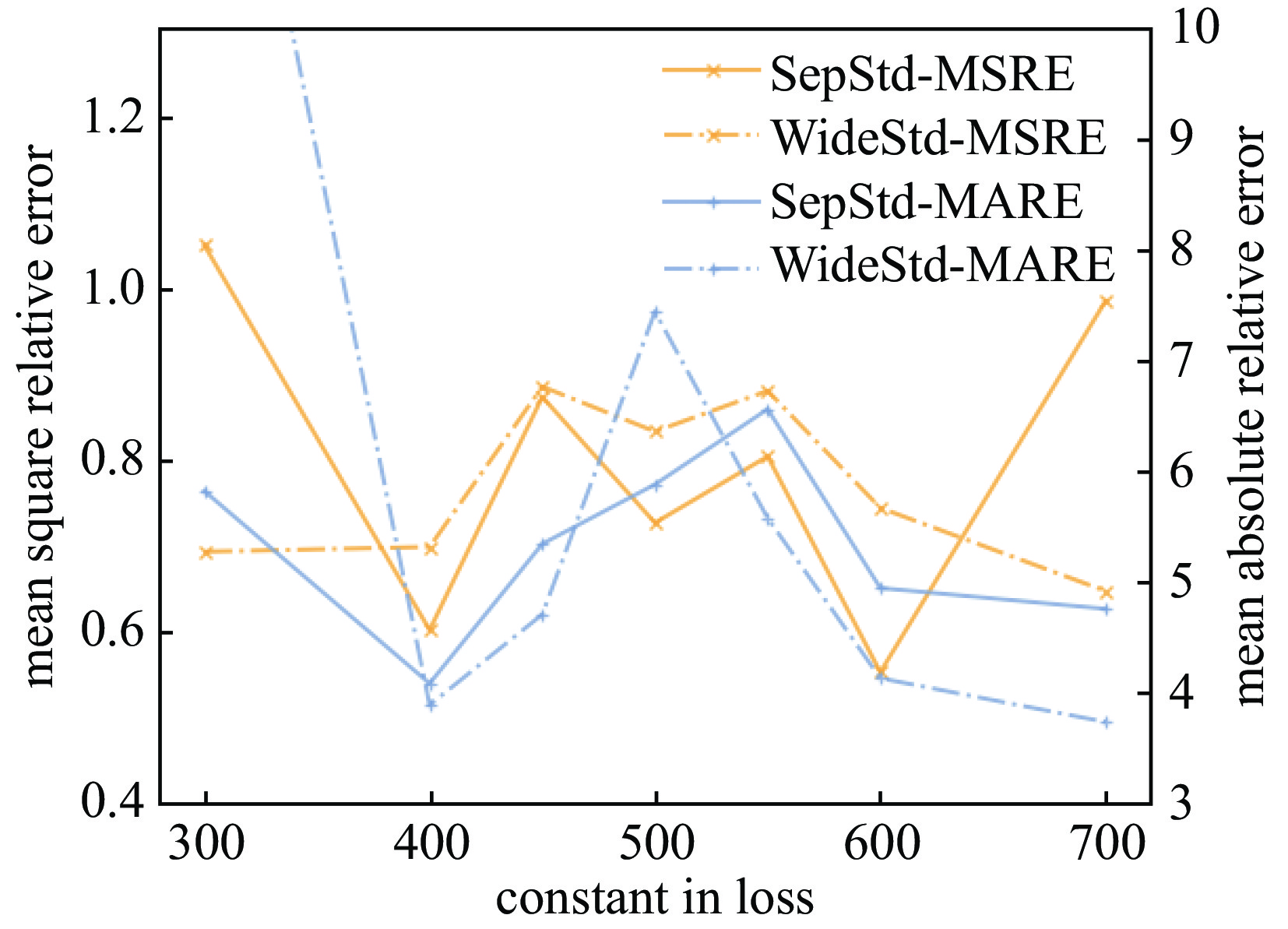
Background The reaction kinetics in lasers often involves a lots of excited state species. The mutual effects and numerical stiffness arising from the excited state species pose significant challenges in numerical simulations of lasers. The development of artificial intelligence has made Neural Networks (NNs) a promising approach to address the computational intensity and instability in Excited State Reaction Kinetics (ESRK).Purpose However, the complexity of ESRK poses challenges for NN training. These reactions involve numerous species and mutual effects, resulting in a high-dimensional variable space. This demands that the NN possess the capability to establish complex mapping relationships. Moreover, the significant change in state before and after the reaction leads to a broad variable space coverage, which amplifies the demand for NN's accuracy.Methods To address the aforementioned challenges, this study introduces the successful sequence-to-sequence learning from large language learning into ESRK to enhance prediction accuracy in complex, high-dimensional regression. Additionally, a statistical regularization method is proposed to improve the diversity of the outputs. NNs with different architectures were trained using randomly sampled data, and their capabilities were compared and analyzed.Results The proposed method is validated using a vibrational reaction mechanism for hydrogen fluoride, which involves 16 species and 137 reactions. The results demonstrate that the sequential model achieves lower training loss and relative error during training. Furthermore, experiments with different hyperparameters reveal that variation in the random seed can significantly impact model performance.Conclusions In this work, the introduction of the sequential model successfully reduced the parameter count of the conventional wide model without compromising accuracy. However, due to the intrinsic complexity of ESRK, there remains considerable room for improvement in NN-based regression tasks for this domain.-
Key words:
- excited state /
- reaction kinetics /
- sequence-to-sequence learning /
- complexity
-
Figure 5. The relative errors of neural networks with different constant in regularization
Figure 6. The mean square relative errors on test data of neural networks trained with another random seed
Figure 7. The relative errors on random sampling data of neural networks trained with another random seed
Figure 8. The relative errors of different constant regularized neural networks trained with another random seed
Table 1. The ranges of flow states as the neural network’s inputs
name T / K P / pa $ {Y}_{{{\mathrm{H}}_{2}}} $ $ {Y}_{{{\mathrm{H}}_{2}}\left(1\right)} $ $ {Y}_{\mathrm{H}} $ $ {Y}_{{{\mathrm{F}}_{2}}} $ $ {Y}_{\mathrm{F}} $ $ {Y}_{\text{DF}} $ $ {Y}_{\text{HF}\left(0\right)} $ lower limit $ 3.0\times {10}^{1} $ $ 1.0\times {10}^{2} $ $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ upper limit $ 1.0\times {10}^{3} $ $ 3.5\times {10}^{3} $ $ 5.0\times {10}^{-1} $ $ 5.0\times {10}^{-3} $ $ 1.2\times {10}^{-2} $ $ 3.0\times {10}^{-3} $ $ 3.0\times {10}^{-1} $ $ 5.0\times {10}^{-1} $ $ 2.0\times {10}^{-1} $ name $ {Y}_{\text{HF}\left(1\right)} $ $ {Y}_{\text{HF}\left(2\right)} $ $ {Y}_{\text{HF}\left(3\right)} $ $ {Y}_{\text{HF}\left(4\right)} $ $ {Y}_{\text{HF}\left(5\right)} $ $ {Y}_{\text{HF}\left(6\right)} $ $ {Y}_{\text{HF}\left(7\right)} $ $ {Y}_{\text{He}} $ $ {Y}_{{{\mathrm{N}}_{2}}} $ lower limit $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ $ 0.0\times {10}^{0} $ upper limit $ 7.5\times {10}^{-2} $ $ 1.5\times {10}^{-1} $ $ 4.0\times {10}^{-2} $ $ 3.0\times {10}^{-4} $ $ 2.0\times {10}^{-4} $ $ 1.5\times {10}^{-4} $ $ 1.0\times {10}^{-4} $ $ 9.0\times {10}^{-1} $ $ 2.0\times {10}^{-1} $ 
下载: 导出CSV
Table 2. The configurations of different neural networks
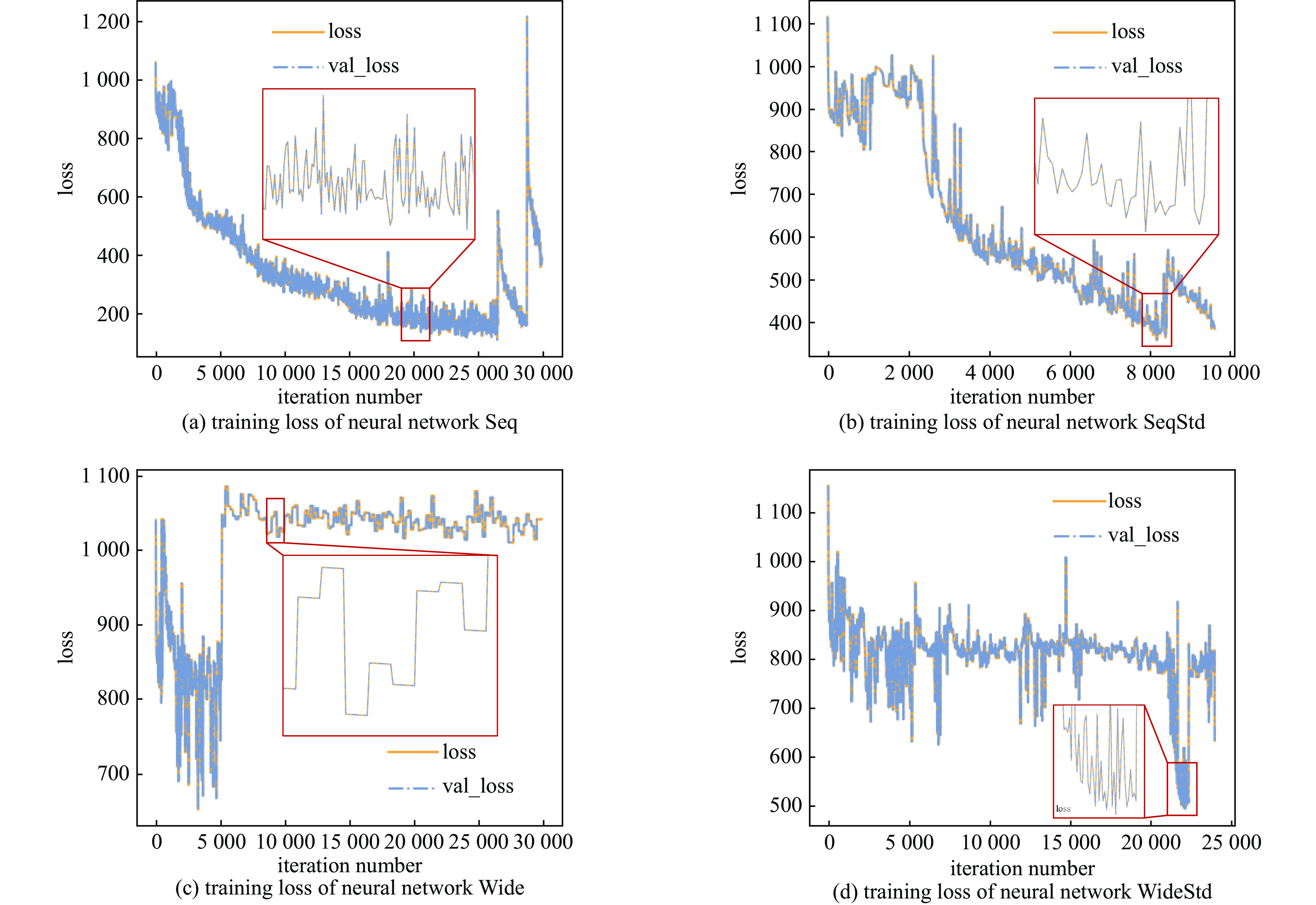
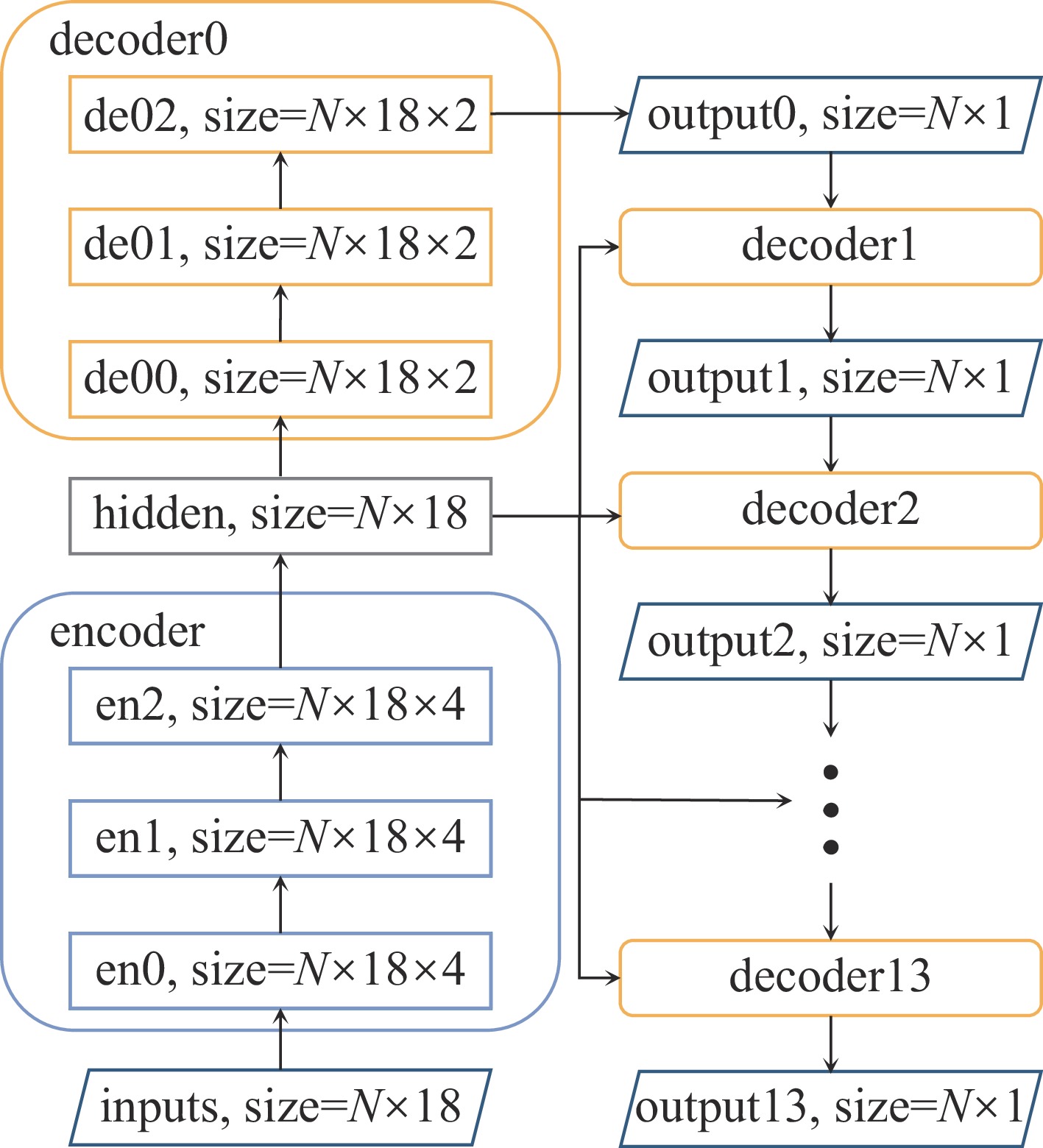
name structure loss total parameters Seq Serial decoders MAE 57631 SeqStd Serial decoders MAE+C 57631 Wide Parallel decoders MAE 467167 WideStd Parallel decoders MAE+C 467167
下载: 导出CSV
-
[1] Waichman K, Barmashenko B D, Rosenwaks S. Comparing modeling and measurements of the output power in chemical oxygen-iodine lasers: a stringent test of I2 dissociation mechanisms[J]. The Journal of Chemical Physics, 2010, 133: 084301. doi: 10.1063/1.3480397 [2] Li Hui, Zhao Tianliang, Li Jiaxu, et al. State-to-state chemical kinetic mechanism for HF chemical lasers[J]. Combustion Theory and Modelling, 2020, 24(1): 129-141. doi: 10.1080/13647830.2019.1662490 [3] D’Alessio G, Sundaresan S, Mueller M E. Automated and efficient local adaptive regression for principal component-based reduced-order modeling of turbulent reacting flows[J]. Proceedings of the Combustion Institute, 2023, 39(4): 5249-5258. doi: 10.1016/j.proci.2022.07.235 [4] Kochkov D, Smith J A, Alieva A, et al. Machine learning–accelerated computational fluid dynamics[J]. Proceedings of the National Academy of Sciences of the United States of America, 2021, 118: e2101784118. [5] Ding Tianjie, Readshaw T, Rigopoulos S, et al. Machine learning tabulation of thermochemistry in turbulent combustion: an approach based on hybrid flamelet/random data and multiple multilayer perceptrons[J]. Combustion and Flame, 2021, 231: 111493. doi: 10.1016/j.combustflame.2021.111493 [6] Ortega A G, Shirin A. Neural network-based descent control for Landers with sloshing and mass variation: a cascade and adaptive PID strategy[J]. Aerospace, 2024, 11: 1009. doi: 10.3390/aerospace11121009 [7] Zhang Shihong, Zhang Chi, Wang Bosen. CRK-PINN: a physics-informed neural network for solving combustion reaction kinetics ordinary differential equations[J]. Combustion and Flame, 2024, 269: 113647. doi: 10.1016/j.combustflame.2024.113647 [8] Hughes G. On the mean accuracy of statistical pattern recognizers[J]. IEEE Transactions on Information Theory, 1968, 14(1): 55-63. doi: 10.1109/TIT.1968.1054102 [9] Han Peilun, Shen Xiaoqian, Shen Boxiong. A simulation study on NOx reduction efficiency in SCR catalysts utilizing a modern C3-CNN algorithm[J]. Fuel, 2024, 363: 130985. doi: 10.1016/j.fuel.2024.130985 [10] Ihme M, Chung W T, Mishra A A. Combustion machine learning: principles, progress and prospects[J]. Progress in Energy and Combustion Science, 2022, 91: 101010. doi: 10.1016/j.pecs.2022.101010 [11] Shin J, Hansinger M, Pfitzner M, et al. A priori analysis on deep learning of filtered reaction rate[J]. Flow, Turbulence and Combustion, 2022, 109(2): 383-409. doi: 10.1007/s10494-022-00330-0 [12] Zhang Tianhan, Yi Yuxiao, Xu Yifan, et al. A multi-scale sampling method for accurate and robust deep neural network to predict combustion chemical kinetics[J]. Combustion and Flame, 2022, 245: 112319. doi: 10.1016/j.combustflame.2022.112319 [13] Bai Tianzi, Huai Ying, Liu Tingting, et al. Acceleration of the complex reacting flow simulation with a generalizable neural network based on meta-learning[J]. Fuel, 2024, 372: 132173. doi: 10.1016/j.fuel.2024.132173 [14] Kretzschmar R, Karayiannis N B, Eggimann F. Feedforward neural network models for handling class overlap and class imbalance[J]. International Journal of Neural Systems, 2005, 15(5): 323-338. doi: 10.1142/S012906570500030X [15] Baskerville N P, Granziol D, Keating J P. Appearance of Random Matrix Theory in deep learning[J]. Physica A: Statistical Mechanics and its Applications, 2022, 590: 126742. doi: 10.1016/j.physa.2021.126742 [16] Zhang Yu, Du Wenli. Intelligent time-scale operator-splitting integration for chemical reaction systems[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(8): 3366-3376. doi: 10.1109/TNNLS.2020.3006348 [17] Marcato A, Santos J E, Boccardo G, et al. Prediction of local concentration fields in porous media with chemical reaction using a multi scale convolutional neural network[J]. Chemical Engineering Journal, 2023, 455: 140367. doi: 10.1016/j.cej.2022.140367 [18] Sun Jie, Wang Yiqing, Tian Baolin, et al. DetonationFoam: an open-source solver for simulation of gaseous detonation based on OpenFOAM[J]. Computer Physics Communications, 2023, 292: 108859. doi: 10.1016/j.cpc.2023.108859 [19] Salunkhe A, Deighan D, DesJardin P E, et al. Physics informed machine learning for chemistry tabulation[J]. Journal of Computational Science, 2023, 69: 102001. doi: 10.1016/j.jocs.2023.102001 [20] Xu Kailai, Darve E. Physics constrained learning for data-driven inverse modeling from sparse observations[J]. Journal of Computational Physics, 2022, 453: 110938. doi: 10.1016/j.jcp.2021.110938 [21] Sutskever I, Vinyals O, Le Q V. Sequence to Sequence Learning with Neural Networks[C]//Proceedings of the 28th International Conference on Neural Information Processing Systems. 2014: 3104-3112. [22] Liu Bowen, Ramsundar B, Kawthekar P, et al. Retrosynthetic reaction prediction using neural sequence-to-sequence models[J]. ACS Central Science, 2017, 3(10): 1103-1113. doi: 10.1021/acscentsci.7b00303 [23] Manke II G C, Hager G D. A review of recent experiments and calculations relevant to the kinetics of the HF laser[J]. Journal of Physical and Chemical Reference Data, 2001, 30(3): 713-733. doi: 10.2514/6.2002-2219 [24] Abadi M, Barham P, Chen Jianmin, et al. TensorFlow: a system for large-scale machine learning[C]//Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation. 2016: 265-283. [25] Goodwin D G, Moffat H K, Speth R L. Cantera: an object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes[R]. Version 2.2. 0, 2015. -
点击查看大图
图(8) / 表(2)
计量
- 文章访问数: 17
- HTML全文浏览量: 9
- PDF下载量: 0
- 被引次数: 0
